
Question and Answers Forum
Question Number 32483 by prof Abdo imad last updated on 25/Mar/18
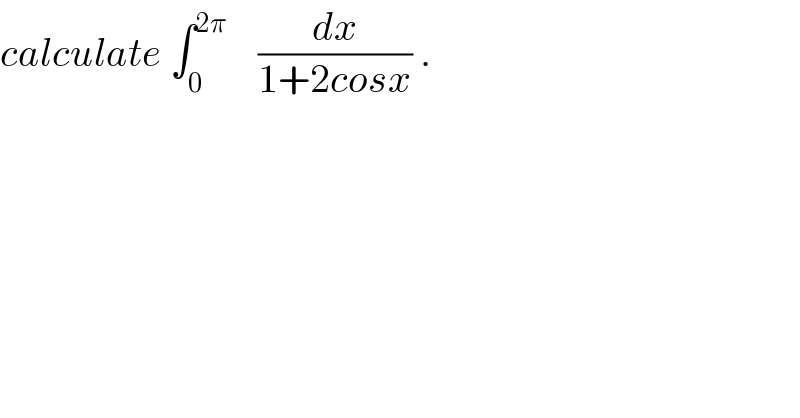
Commented by prof Abdo imad last updated on 26/Mar/18
![let put I = ∫_0 ^(2π) (dx/(1+2cosx)) the ch. x=π +t give I = ∫_(−π) ^π (dt/(1−2cost)) = 2 ∫_0 ^π (dt/(1−2cost)) and the ch. tan((t/2))=u hive I = 2 ∫_0 ^(+∞) (1/(1−2((1−u^2 )/(1+u^2 )))) ((2du)/(1+u^2 )) = 4 ∫_0 ^∞ (du/(1+u^2 −2 +2u^2 )) = 4∫_0 ^∞ (du/(3u^2 −1)) = 4 ∫_0 ^∞ (du/(((√3) u +1)((√3) −1))) =2 ∫_0 ^∞ ( (1/((√3) t −1)) −(1/((√3) t+1)))du =(2/(√3))[ ln∣(((√3)t−1)/((√3)t +1))∣]_0 ^(+∞) =0 I =0](Q32507.png)
Commented by prof Abdo imad last updated on 26/Mar/18

| ||
Question and Answers Forum | ||
Question Number 32483 by prof Abdo imad last updated on 25/Mar/18 | ||
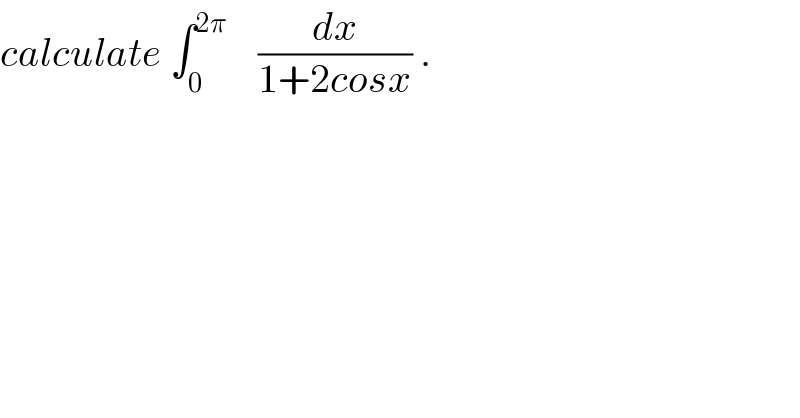 | ||
Commented by prof Abdo imad last updated on 26/Mar/18 | ||
![let put I = ∫_0 ^(2π) (dx/(1+2cosx)) the ch. x=π +t give I = ∫_(−π) ^π (dt/(1−2cost)) = 2 ∫_0 ^π (dt/(1−2cost)) and the ch. tan((t/2))=u hive I = 2 ∫_0 ^(+∞) (1/(1−2((1−u^2 )/(1+u^2 )))) ((2du)/(1+u^2 )) = 4 ∫_0 ^∞ (du/(1+u^2 −2 +2u^2 )) = 4∫_0 ^∞ (du/(3u^2 −1)) = 4 ∫_0 ^∞ (du/(((√3) u +1)((√3) −1))) =2 ∫_0 ^∞ ( (1/((√3) t −1)) −(1/((√3) t+1)))du =(2/(√3))[ ln∣(((√3)t−1)/((√3)t +1))∣]_0 ^(+∞) =0 I =0](Q32507.png) | ||
Commented by prof Abdo imad last updated on 26/Mar/18 | ||
 | ||