
Question and Answers Forum
Question Number 32484 by Eng.Firas last updated on 25/Mar/18
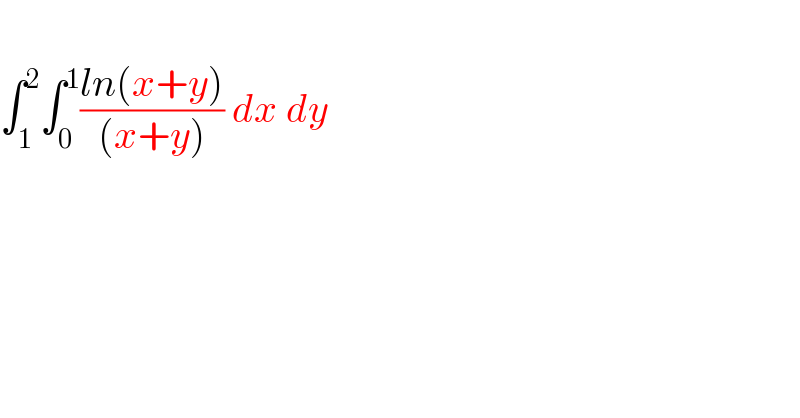
Commented by abdo imad last updated on 26/Mar/18
![I =∫_1 ^2 ( ∫_0 ^1 ((ln(x+y))/(x+y))dx)dy let put A= ∫_0 ^1 ((ln(x+y))/(x+y))dx ch. x+y =t give A = ∫_y ^(1+y) ((lnt)/t) dt =[(1/2)( lnt)^2 ]_y ^(1+y) =(1/2) ( (ln(1+y)^2 −(lny)^2 ) ⇒ I = (1/2) ∫_1 ^2 (ln(1+y))^2 dy − (1/2) ∫_1 ^2 ((lny))^2 dy but ch. lny =t give ∫_1 ^2 (lny)^2 dy = ∫_0 ^(ln(2)) t^2 e^t dt = [t^2 e^t ]_0 ^(ln(2)) −∫_0 ^(ln(2)) 2t e^t dt = 2(ln2)^2 −2 ( [t e^t ]_0 ^(ln(2)) −∫_0 ^(ln(2)) e^t dt) =2(ln2)^2 −2 (2ln2 −1)= 2(ln2)^2 −4ln(2) +1 also ch. ln(1+y) =t give ∫_1 ^2 (ln(1+y))^2 dy = ∫_(ln2) ^(ln(3)) t^2 e^t dt and we get the value of this intevral by the same method.....](Q32488.png)
Commented by Eng.Firas last updated on 26/Mar/18

| ||
Question and Answers Forum | ||
Question Number 32484 by Eng.Firas last updated on 25/Mar/18 | ||
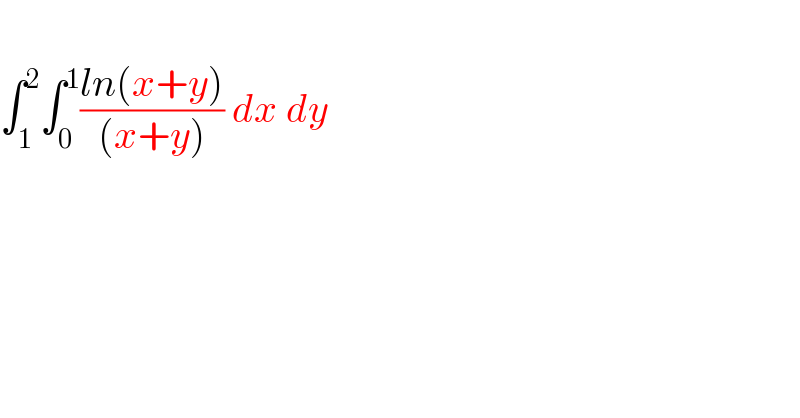 | ||
Commented by abdo imad last updated on 26/Mar/18 | ||
![I =∫_1 ^2 ( ∫_0 ^1 ((ln(x+y))/(x+y))dx)dy let put A= ∫_0 ^1 ((ln(x+y))/(x+y))dx ch. x+y =t give A = ∫_y ^(1+y) ((lnt)/t) dt =[(1/2)( lnt)^2 ]_y ^(1+y) =(1/2) ( (ln(1+y)^2 −(lny)^2 ) ⇒ I = (1/2) ∫_1 ^2 (ln(1+y))^2 dy − (1/2) ∫_1 ^2 ((lny))^2 dy but ch. lny =t give ∫_1 ^2 (lny)^2 dy = ∫_0 ^(ln(2)) t^2 e^t dt = [t^2 e^t ]_0 ^(ln(2)) −∫_0 ^(ln(2)) 2t e^t dt = 2(ln2)^2 −2 ( [t e^t ]_0 ^(ln(2)) −∫_0 ^(ln(2)) e^t dt) =2(ln2)^2 −2 (2ln2 −1)= 2(ln2)^2 −4ln(2) +1 also ch. ln(1+y) =t give ∫_1 ^2 (ln(1+y))^2 dy = ∫_(ln2) ^(ln(3)) t^2 e^t dt and we get the value of this intevral by the same method.....](Q32488.png) | ||
Commented by Eng.Firas last updated on 26/Mar/18 | ||
 | ||