Question and Answers Forum

All Questions      Topic List

Mensuration Questions

Previous in All Question      Next in All Question      

Previous in Mensuration      Next in Mensuration      

Question Number 3250 by Filup last updated on 08/Dec/15

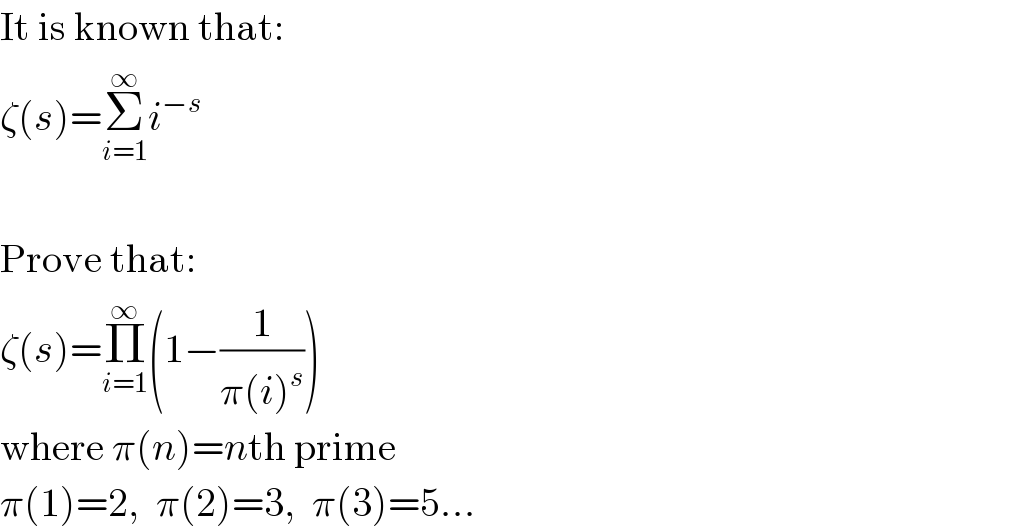
It is known that: ζ(s)=Σ_(i=1) ^∞ i^(−s) Prove that: ζ(s)=Π_(i=1) ^∞ (1−(1/(π(i)^s ))) where π(n)=nth prime π(1)=2, π(2)=3, π(3)=5...

$$\mathrm{It}\:\mathrm{is}\:\mathrm{known}\:\mathrm{that}: \\ $$$$\zeta\left({s}\right)=\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}{i}^{−{s}} \\ $$$$ \\ $$$$\mathrm{Prove}\:\mathrm{that}: \\ $$$$\zeta\left({s}\right)=\underset{{i}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\mathrm{1}−\frac{\mathrm{1}}{\pi\left({i}\right)^{{s}} }\right) \\ $$$$\mathrm{where}\:\pi\left({n}\right)={n}\mathrm{th}\:\mathrm{prime} \\ $$$$\pi\left(\mathrm{1}\right)=\mathrm{2},\:\:\pi\left(\mathrm{2}\right)=\mathrm{3},\:\:\pi\left(\mathrm{3}\right)=\mathrm{5}... \\ $$

Commented by 123456 last updated on 08/Dec/15

Σ_(n≥1) (1/n^s )=Π_(p∈P) (1/(1−p^(−s) )) ζ(s)=Π_(p∈P) (1/(1−p^(−s) )) (1/(ζ(s)))=Π_(p∈P) 1−p^(−s)

$$\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{n}^{{s}} }=\underset{{p}\in\mathbb{P}} {\prod}\frac{\mathrm{1}}{\mathrm{1}−{p}^{−{s}} } \\ $$$$\zeta\left({s}\right)=\underset{{p}\in\mathbb{P}} {\prod}\frac{\mathrm{1}}{\mathrm{1}−{p}^{−{s}} } \\ $$$$\frac{\mathrm{1}}{\zeta\left({s}\right)}=\underset{{p}\in\mathbb{P}} {\prod}\mathrm{1}−{p}^{−{s}} \\ $$

Answered by prakash jain last updated on 08/Dec/15

ζ(s)=(1/1^s )+(1/2^s )+(1/3^s )+(1/4^s )+.. (1/2^s )ζ(s)=(1/2^s )+(1/4^s )+(1/6^s )+.. (1−(1/2^s ))ζ(s)=1+(1/3^s )+(1/5^s )+... (all factors of (1/2^s ) removed) (1−(1/3^s ))(1−(1/2^s ))ζ(s)=1+(1/5^s )+... (all multiples of 3^s removed) repeating the process for all primes number each step remove multiples of a prime number ζ(s)Π_(i=1) ^∞ (1−(1/(π(i)^s )))=1 (1/(ζ(s)))=Π_(i=1) ^∞ (1−(1/(π(i)^s ))) (1/(ζ(s)))=Π_(i=1) ^∞ (1−π(i)^(−s) ) As mentioned in the question π(i) is ith prime. Usual convention is π is prime density.

$$\zeta\left({s}\right)=\frac{\mathrm{1}}{\mathrm{1}^{{s}} }+\frac{\mathrm{1}}{\mathrm{2}^{{s}} }+\frac{\mathrm{1}}{\mathrm{3}^{{s}} }+\frac{\mathrm{1}}{\mathrm{4}^{{s}} }+.. \\ $$$$\frac{\mathrm{1}}{\mathrm{2}^{{s}} }\zeta\left({s}\right)=\frac{\mathrm{1}}{\mathrm{2}^{{s}} }+\frac{\mathrm{1}}{\mathrm{4}^{{s}} }+\frac{\mathrm{1}}{\mathrm{6}^{{s}} }+.. \\ $$$$\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{{s}} }\right)\zeta\left({s}\right)=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}^{{s}} }+\frac{\mathrm{1}}{\mathrm{5}^{{s}} }+...\:\left({all}\:{factors}\:{of}\:\frac{\mathrm{1}}{\mathrm{2}^{{s}} }\:{removed}\right) \\ $$$$\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}^{{s}} }\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{{s}} }\right)\zeta\left({s}\right)=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{5}^{{s}} }+...\:\left({all}\:{multiples}\:{of}\:\mathrm{3}^{{s}} \:{removed}\right) \\ $$$${repeating}\:{the}\:{process}\:{for}\:{all}\:{primes}\:{number} \\ $$$${each}\:{step}\:{remove}\:{multiples}\:{of}\:{a}\:{prime}\:{number} \\ $$$$\zeta\left({s}\right)\underset{{i}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\mathrm{1}−\frac{\mathrm{1}}{\pi\left({i}\right)^{{s}} }\right)=\mathrm{1} \\ $$$$\frac{\mathrm{1}}{\zeta\left({s}\right)}=\underset{{i}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\mathrm{1}−\frac{\mathrm{1}}{\pi\left({i}\right)^{{s}} }\right) \\ $$$$\frac{\mathrm{1}}{\zeta\left({s}\right)}=\underset{{i}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\mathrm{1}−\pi\left({i}\right)^{−{s}} \right) \\ $$$$\mathrm{As}\:\mathrm{mentioned}\:\mathrm{in}\:\mathrm{the}\:\mathrm{question}\:\pi\left({i}\right)\:\mathrm{is}\:{i}\mathrm{th}\:\mathrm{prime}. \\ $$$$\mathrm{Usual}\:\mathrm{convention}\:\mathrm{is}\:\pi\:\mathrm{is}\:\mathrm{prime}\:\mathrm{density}. \\ $$

Commented by RasheedAhmad last updated on 08/Dec/15

ζ(s)=(1/2^s )+(1/2^s )+(1/3^s )+(1/4^s )+.. ⇒^? (1/2^s )ζ(s)=(1/2^s )+(1/4^s )+(1/6^s )+..

$$\zeta\left({s}\right)=\frac{\mathrm{1}}{\mathrm{2}^{{s}} }+\frac{\mathrm{1}}{\mathrm{2}^{{s}} }+\frac{\mathrm{1}}{\mathrm{3}^{{s}} }+\frac{\mathrm{1}}{\mathrm{4}^{{s}} }+.. \\ $$$$\overset{?} {\Rightarrow}\frac{\mathrm{1}}{\mathrm{2}^{{s}} }\zeta\left({s}\right)=\frac{\mathrm{1}}{\mathrm{2}^{{s}} }+\frac{\mathrm{1}}{\mathrm{4}^{{s}} }+\frac{\mathrm{1}}{\mathrm{6}^{{s}} }+.. \\ $$

Commented by prakash jain last updated on 08/Dec/15

typo. corrected.

$${typo}.\:{corrected}. \\ $$

Commented by Filup last updated on 08/Dec/15

Amazing!

$${Amazing}! \\ $$

Commented by Filup last updated on 08/Dec/15

I am aware π(i) is the prime density. But I have seen π(i) be used on several occasions as the nth prime. But If it is more aesthetic, i′ll stick to P(i)=ith prime :) Thank you regardess!

$$\mathrm{I}\:\mathrm{am}\:\mathrm{aware}\:\pi\left({i}\right)\:\mathrm{is}\:\mathrm{the}\:{prime}\:{density}. \\ $$$$\mathrm{But}\:\mathrm{I}\:\mathrm{have}\:\mathrm{seen}\:\pi\left({i}\right)\:\mathrm{be}\:\mathrm{used}\:\mathrm{on}\:\mathrm{several} \\ $$$$\mathrm{occasions}\:\mathrm{as}\:\mathrm{the}\:{n}\mathrm{th}\:\mathrm{prime}. \\ $$$$\mathrm{But}\:\mathrm{If}\:\mathrm{it}\:\mathrm{is}\:\mathrm{more}\:\mathrm{aesthetic},\:\mathrm{i}'\mathrm{ll}\:\mathrm{stick}\:\mathrm{to} \\ $$$$\left.{P}\left({i}\right)={i}\mathrm{th}\:\mathrm{prime}\::\right) \\ $$$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{regardess}! \\ $$

Answered by 123456 last updated on 08/Dec/15

you can go by other way too note that (1/(1−q))=1+q+q^2 +... (∣q∣<1) so (1/(1−p^(−s) ))=1+(1/p^s )+(1/p^(2s) )+... (s>1 and since p>1⇒1/p<1) (1/(1−p^(−s) ))=Σ_(n=0) ^(+∞) p^(−ns) Π_(p∈P) (1/(1−p^(−s) ))=Π_(p∈P) Σ_(n=0) ^(+∞) p^(−ns) by unique factorization we have Π_(p∈P) (1/(1−p^(−s) ))=Σ_(n=0) ^(+∞) n^(−s) =ζ(s) (1/(ζ(s)))=Π_(p∈P) 1−p^(−s)

$$\mathrm{you}\:\mathrm{can}\:\mathrm{go}\:\mathrm{by}\:\mathrm{other}\:\mathrm{way}\:\mathrm{too} \\ $$$$\mathrm{note}\:\mathrm{that} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}−{q}}=\mathrm{1}+{q}+{q}^{\mathrm{2}} +...\:\:\:\left(\mid{q}\mid<\mathrm{1}\right) \\ $$$$\mathrm{so} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}−{p}^{−{s}} }=\mathrm{1}+\frac{\mathrm{1}}{{p}^{{s}} }+\frac{\mathrm{1}}{{p}^{\mathrm{2}{s}} }+...\:\left({s}>\mathrm{1}\:\mathrm{and}\:\mathrm{since}\:{p}>\mathrm{1}\Rightarrow\mathrm{1}/{p}<\mathrm{1}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{1}−{p}^{−{s}} }=\underset{{n}=\mathrm{0}} {\overset{+\infty} {\sum}}{p}^{−{ns}} \\ $$$$\underset{{p}\in\mathbb{P}} {\prod}\frac{\mathrm{1}}{\mathrm{1}−{p}^{−{s}} }=\underset{{p}\in\mathbb{P}} {\prod}\underset{{n}=\mathrm{0}} {\overset{+\infty} {\sum}}{p}^{−{ns}} \\ $$$$\mathrm{by}\:\mathrm{unique}\:\mathrm{factorization}\:\mathrm{we}\:\mathrm{have} \\ $$$$\underset{{p}\in\mathbb{P}} {\prod}\frac{\mathrm{1}}{\mathrm{1}−{p}^{−{s}} }=\underset{{n}=\mathrm{0}} {\overset{+\infty} {\sum}}{n}^{−{s}} =\zeta\left({s}\right) \\ $$$$\frac{\mathrm{1}}{\zeta\left({s}\right)}=\underset{{p}\in\mathbb{P}} {\prod}\mathrm{1}−{p}^{−{s}} \\ $$

Commented by Filup last updated on 08/Dec/15

Awesome!

$${Awesome}! \\ $$

Commented by prakash jain last updated on 20/May/17

123456, are u still using app?

$$\mathrm{123456},\:\mathrm{are}\:\mathrm{u}\:\mathrm{still}\:\mathrm{using}\:\mathrm{app}? \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com