Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 32734 by caravan msup abdo. last updated on 01/Apr/18

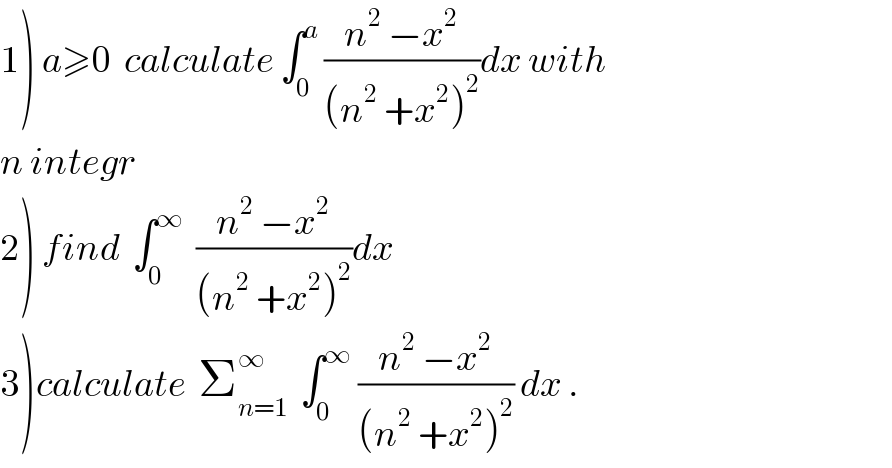
1) a≥0 calculate ∫_0 ^a ((n^2 −x^2 )/((n^2 +x^2 )^2 ))dx with n integr 2) find ∫_0 ^∞ ((n^2 −x^2 )/((n^2 +x^2 )^2 ))dx 3)calculate Σ_(n=1) ^∞ ∫_0 ^∞ ((n^2 −x^2 )/((n^2 +x^2 )^2 )) dx .

$$\left.\mathrm{1}\right)\:{a}\geqslant\mathrm{0}\:\:{calculate}\:\int_{\mathrm{0}} ^{{a}} \:\frac{{n}^{\mathrm{2}} \:−{x}^{\mathrm{2}} }{\left({n}^{\mathrm{2}} \:+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx}\:{with} \\ $$$${n}\:{integr} \\ $$$$\left.\mathrm{2}\right)\:{find}\:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{n}^{\mathrm{2}} \:−{x}^{\mathrm{2}} }{\left({n}^{\mathrm{2}} \:+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx} \\ $$$$\left.\mathrm{3}\right){calculate}\:\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\int_{\mathrm{0}} ^{\infty} \:\frac{{n}^{\mathrm{2}} \:−{x}^{\mathrm{2}} }{\left({n}^{\mathrm{2}} \:+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:{dx}\:. \\ $$

Commented by abdo imad last updated on 08/Apr/18

let put I_n (a) = ∫_0 ^a ((n^2 −x^2 )/((n^2 +x^2 )))dx I_n (a) =n^2 ∫_0 ^a (dx/((n^2 +x^2 )^2 )) − ∫_0 ^a ((n^2 +x^2 −n^2 )/((n^2 +x^2 )))dx =2n^2 ∫_0 ^a (dx/((n^2 +x^2 )^2 )) −∫_0 ^a (dx/(n^2 +x^2 )) .ch.x=nt give ∫_0 ^a (dx/(n^2 +x^2 )) = ∫_0 ^(a/n) ((ndt)/(n^2 (1+t^2 ))) =(1/n) arctan((a/n)) also ∫_0 ^a (dx/((n^2 +x^2 )^2 )) = ∫_0 ^(a/n) ((ndt)/(n^4 ( 1+t^2 )^2 )) = (1/n^3 ) ∫_0 ^(a/n) (dt/((1+t^2 )^2 )) =_(t=tanθ) (1/n^3 ) ∫_0 ^(arctan((a/n))) (((1+tan^2 θ)dθ)/((1+tan^2 θ)^2 )) = (1/n^3 ) ∫_0 ^(arctan((a/n))) (dθ/(1+tan^2 θ)) =(1/n^3 ) ∫_0 ^(arctan((a/n))) (cos^2 θ)dθ =(1/(2n^3 )) ∫_0 ^(arctan((a/n))) (1+cos(2θ))dθ = ((arctan((a/n)))/(2n^3 )) + (1/(4n^3 )) [sin(2θ)]_0 ^(arctan((a/n))) = ((arctan((a/n)))/(2n^3 )) +(1/(4n^3 )) sin(2arctan((a/n)))⇒ I_n (a) = ((arctan((a/n)))/n) + (1/(2n)) sin(2arctan((a/n))) −(1/n) arctan((a/n)) I_n (a) = (1/(2n)) sin (2 arctan((a/n))) .

$${let}\:{put}\:{I}_{{n}} \left({a}\right)\:=\:\int_{\mathrm{0}} ^{{a}} \:\:\frac{{n}^{\mathrm{2}} \:−{x}^{\mathrm{2}} }{\left({n}^{\mathrm{2}} \:+{x}^{\mathrm{2}} \right)}{dx}\: \\ $$$${I}_{{n}} \left({a}\right)\:={n}^{\mathrm{2}} \:\int_{\mathrm{0}} ^{{a}} \:\:\:\frac{{dx}}{\left({n}^{\mathrm{2}} \:+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:\:−\:\int_{\mathrm{0}} ^{{a}} \:\frac{{n}^{\mathrm{2}} \:+{x}^{\mathrm{2}} \:−{n}^{\mathrm{2}} }{\left({n}^{\mathrm{2}} \:+{x}^{\mathrm{2}} \right)}{dx} \\ $$$$=\mathrm{2}{n}^{\mathrm{2}} \:\int_{\mathrm{0}} ^{{a}} \:\:\:\frac{{dx}}{\left({n}^{\mathrm{2}} \:+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:−\int_{\mathrm{0}} ^{{a}} \:\:\frac{{dx}}{{n}^{\mathrm{2}} \:+{x}^{\mathrm{2}} }\:\:.{ch}.{x}={nt}\:{give} \\ $$$$\int_{\mathrm{0}} ^{{a}} \:\:\:\frac{{dx}}{{n}^{\mathrm{2}} \:+{x}^{\mathrm{2}} }\:=\:\int_{\mathrm{0}} ^{\frac{{a}}{{n}}} \:\:\:\:\frac{{ndt}}{{n}^{\mathrm{2}} \left(\mathrm{1}+{t}^{\mathrm{2}} \right)}\:=\frac{\mathrm{1}}{{n}}\:{arctan}\left(\frac{{a}}{{n}}\right)\:{also} \\ $$$$\int_{\mathrm{0}} ^{{a}} \:\:\:\:\frac{{dx}}{\left({n}^{\mathrm{2}} \:+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:=\:\int_{\mathrm{0}} ^{\frac{{a}}{{n}}} \:\:\:\frac{{ndt}}{{n}^{\mathrm{4}} \left(\:\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\:=\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\:\int_{\mathrm{0}} ^{\frac{{a}}{{n}}} \:\:\:\frac{{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$=_{{t}={tan}\theta} \:\:\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\:\int_{\mathrm{0}} ^{{arctan}\left(\frac{{a}}{{n}}\right)} \:\:\:\:\:\:\frac{\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right){d}\theta}{\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right)^{\mathrm{2}} } \\ $$$$=\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\:\int_{\mathrm{0}} ^{{arctan}\left(\frac{{a}}{{n}}\right)} \:\:\:\frac{{d}\theta}{\mathrm{1}+{tan}^{\mathrm{2}} \theta}\:=\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\:\int_{\mathrm{0}} ^{{arctan}\left(\frac{{a}}{{n}}\right)} \:\left({cos}^{\mathrm{2}} \theta\right){d}\theta \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{n}^{\mathrm{3}} }\:\int_{\mathrm{0}} ^{{arctan}\left(\frac{{a}}{{n}}\right)} \:\left(\mathrm{1}+{cos}\left(\mathrm{2}\theta\right)\right){d}\theta \\ $$$$=\:\frac{{arctan}\left(\frac{{a}}{{n}}\right)}{\mathrm{2}{n}^{\mathrm{3}} }\:\:\:+\:\frac{\mathrm{1}}{\mathrm{4}{n}^{\mathrm{3}} }\:\left[{sin}\left(\mathrm{2}\theta\right)\right]_{\mathrm{0}} ^{{arctan}\left(\frac{{a}}{{n}}\right)} \\ $$$$=\:\frac{{arctan}\left(\frac{{a}}{{n}}\right)}{\mathrm{2}{n}^{\mathrm{3}} }\:+\frac{\mathrm{1}}{\mathrm{4}{n}^{\mathrm{3}} }\:{sin}\left(\mathrm{2}{arctan}\left(\frac{{a}}{{n}}\right)\right)\Rightarrow \\ $$$${I}_{{n}} \left({a}\right)\:=\:\frac{{arctan}\left(\frac{{a}}{{n}}\right)}{{n}}\:\:+\:\frac{\mathrm{1}}{\mathrm{2}{n}}\:{sin}\left(\mathrm{2}{arctan}\left(\frac{{a}}{{n}}\right)\right)\:−\frac{\mathrm{1}}{{n}}\:{arctan}\left(\frac{{a}}{{n}}\right) \\ $$$${I}_{{n}} \left({a}\right)\:\:=\:\frac{\mathrm{1}}{\mathrm{2}{n}}\:{sin}\:\left(\mathrm{2}\:{arctan}\left(\frac{{a}}{{n}}\right)\right)\:. \\ $$

Commented by abdo imad last updated on 08/Apr/18

we have sin(2arctan((a/n)))=2sin(arctan((a/n)))cos(arctsn((a/n))) but we have the frmulae sin(arctanx)= (x/(√(1+x^2 ))) cos(arctanx) = (1/(√(1+x^2 ))) ⇒ I_n (a) =(1/n) ((a/n)/(√(1+(a^2 /n^2 )))) (1/(√(1+(a^2 /n^2 )))) = (a/((1+(a^2 /n^2 ))))= ((an^2 )/(n^2 +a^2 ))

$${we}\:{have}\:\:{sin}\left(\mathrm{2}{arctan}\left(\frac{{a}}{{n}}\right)\right)=\mathrm{2}{sin}\left({arctan}\left(\frac{{a}}{{n}}\right)\right){cos}\left({arctsn}\left(\frac{{a}}{{n}}\right)\right) \\ $$$${but}\:{we}\:{have}\:{the}\:{frmulae}\:{sin}\left({arctanx}\right)=\:\frac{{x}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }} \\ $$$${cos}\left({arctanx}\right)\:=\:\frac{\mathrm{1}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:\Rightarrow \\ $$$${I}_{{n}} \left({a}\right)\:=\frac{\mathrm{1}}{{n}}\:\:\frac{\frac{{a}}{{n}}}{\sqrt{\mathrm{1}+\frac{{a}^{\mathrm{2}} }{{n}^{\mathrm{2}} }}}\:\:\frac{\mathrm{1}}{\sqrt{\mathrm{1}+\frac{{a}^{\mathrm{2}} }{{n}^{\mathrm{2}} }}}\:=\:\frac{{a}}{\left(\mathrm{1}+\frac{{a}^{\mathrm{2}} }{{n}^{\mathrm{2}} }\right)}=\:\frac{{an}^{\mathrm{2}} }{{n}^{\mathrm{2}} \:+{a}^{\mathrm{2}} } \\ $$

Commented by abdo imad last updated on 08/Apr/18

2) ∫_0 ^∞ ((n^2 −x^2 )/((n^2 +x^2 )^2 )) =lim_(a→+∞) I_n (a) =lim_(a→+∞) ((an^2 )/(n^2 +a^2 )) =lim_(a→+∞) (n^2 /a) =0 .

$$\left.\mathrm{2}\right)\:\int_{\mathrm{0}} ^{\infty} \:\frac{{n}^{\mathrm{2}} \:−{x}^{\mathrm{2}} }{\left({n}^{\mathrm{2}} \:+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:={lim}_{{a}\rightarrow+\infty} \:{I}_{{n}} \left({a}\right)\:={lim}_{{a}\rightarrow+\infty} \:\:\frac{{an}^{\mathrm{2}} }{{n}^{\mathrm{2}} \:+{a}^{\mathrm{2}} } \\ $$$$={lim}_{{a}\rightarrow+\infty} \:\:\frac{{n}^{\mathrm{2}} }{{a}}\:=\mathrm{0}\:. \\ $$

Answered by hknkrc46 last updated on 04/Apr/18

1)x=ntanu⇒dx=n(1+tan^2 u)du=nsec^2 udu x→a,u→arctan((a/n)) ∧ x→0,u→0 ∫_0 ^a ((n^2 −x^2 )/((n^2 +x^2 )^2 ))dx=∫_0 ^(arctan((a/n))) ((n^2 −(ntanu)^2 )/((n^2 +(ntanu)^2 )^2 ))nsec^2 udu =∫_0 ^(arctan((a/n))) ((n^2 −n^2 tan^2 u)/((n^2 +n^2 tan^2 u)^2 ))nsec^2 udu =∫_0 ^(arctan((a/n))) ((n^2 (1−tan^2 u))/((n^2 (1+tan^2 u))^2 ))nsec^2 udu =∫_0 ^(arctan((a/n))) (((n^2 cos2u)/(cos^2 u))/(n^4 sec^4 u))nsec^2 udu =∫_0 ^(arctan((a/n))) ((cos2u)/n)du=((sin2u)/(2n))∣_0 ^(arctan((a/n))) =((sin(2arctan((a/n))))/(2n)) =((sin(arctan((a/n)))cos(arctan((a/n))))/n)=(a/(a^2 +n^2 )) ★ arctan((a/n))=ψ⇒tanψ=(a/n)⇒sinψ=(a/(√(a^2 +n^2 ))) ∧ cosψ=(n/(√(a^2 +n^2 ))) 2)∫_0 ^∞ ((n^2 −x^2 )/((n^2 +x^2 )^2 ))dx=lim_(a→∞) ∫_0 ^a ((n^2 −x^2 )/((n^2 +x^2 )^2 ))dx=lim_(a→∞) (a/(a^2 +n^2 ))=0 3)Σ_(n=1) ^∞ ∫_0 ^∞ ((n^2 −x^2 )/((n^2 +x^2 )^2 ))dx=lim_(k→∞) Σ_(n=1) ^k ∫_0 ^∞ ((n^2 −x^2 )/((n^2 +x^2 )^2 ))dx=0

$$\left.\mathrm{1}\right)\mathrm{x}=\mathrm{ntanu}\Rightarrow\mathrm{dx}=\mathrm{n}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{u}\right)\mathrm{du}=\mathrm{nsec}^{\mathrm{2}} \mathrm{udu} \\ $$$$\mathrm{x}\rightarrow\mathrm{a},\mathrm{u}\rightarrow\mathrm{arctan}\left(\frac{\mathrm{a}}{\mathrm{n}}\right)\:\wedge\:\mathrm{x}\rightarrow\mathrm{0},\mathrm{u}\rightarrow\mathrm{0} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{a}} \frac{\mathrm{n}^{\mathrm{2}} −\mathrm{x}^{\mathrm{2}} }{\left(\mathrm{n}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dx}=\int_{\mathrm{0}} ^{\mathrm{arctan}\left(\frac{\mathrm{a}}{\mathrm{n}}\right)} \frac{\mathrm{n}^{\mathrm{2}} −\left(\mathrm{ntanu}\right)^{\mathrm{2}} }{\left(\mathrm{n}^{\mathrm{2}} +\left(\mathrm{ntanu}\right)^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{nsec}^{\mathrm{2}} \mathrm{udu} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{arctan}\left(\frac{\mathrm{a}}{\mathrm{n}}\right)} \frac{\mathrm{n}^{\mathrm{2}} −\mathrm{n}^{\mathrm{2}} \mathrm{tan}^{\mathrm{2}} \mathrm{u}}{\left(\mathrm{n}^{\mathrm{2}} +\mathrm{n}^{\mathrm{2}} \mathrm{tan}^{\mathrm{2}} \mathrm{u}\right)^{\mathrm{2}} }\mathrm{nsec}^{\mathrm{2}} \mathrm{udu} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{arctan}\left(\frac{\mathrm{a}}{\mathrm{n}}\right)} \frac{\mathrm{n}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \mathrm{u}\right)}{\left(\mathrm{n}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{u}\right)\right)^{\mathrm{2}} }\mathrm{nsec}^{\mathrm{2}} \mathrm{udu} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{arctan}\left(\frac{\mathrm{a}}{\mathrm{n}}\right)} \frac{\frac{\mathrm{n}^{\mathrm{2}} \mathrm{cos2u}}{\mathrm{cos}^{\mathrm{2}} \mathrm{u}}}{\mathrm{n}^{\mathrm{4}} \mathrm{sec}^{\mathrm{4}} \mathrm{u}}\mathrm{nsec}^{\mathrm{2}} \mathrm{udu} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{arctan}\left(\frac{\mathrm{a}}{\mathrm{n}}\right)} \frac{\mathrm{cos2u}}{\mathrm{n}}\mathrm{du}=\frac{\mathrm{sin2u}}{\mathrm{2n}}\mid_{\mathrm{0}} ^{\mathrm{arctan}\left(\frac{\mathrm{a}}{\mathrm{n}}\right)} =\frac{\mathrm{sin}\left(\mathrm{2arctan}\left(\frac{\mathrm{a}}{\mathrm{n}}\right)\right)}{\mathrm{2n}} \\ $$$$=\frac{\mathrm{sin}\left(\mathrm{arctan}\left(\frac{\mathrm{a}}{\mathrm{n}}\right)\right)\mathrm{cos}\left(\mathrm{arctan}\left(\frac{\mathrm{a}}{\mathrm{n}}\right)\right)}{\mathrm{n}}=\frac{\mathrm{a}}{\mathrm{a}^{\mathrm{2}} +\mathrm{n}^{\mathrm{2}} } \\ $$$$\bigstar\:\mathrm{arctan}\left(\frac{\mathrm{a}}{\mathrm{n}}\right)=\psi\Rightarrow\mathrm{tan}\psi=\frac{\mathrm{a}}{\mathrm{n}}\Rightarrow\mathrm{sin}\psi=\frac{\mathrm{a}}{\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{n}^{\mathrm{2}} }}\:\wedge\:\mathrm{cos}\psi=\frac{\mathrm{n}}{\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{n}^{\mathrm{2}} }} \\ $$$$\left.\mathrm{2}\right)\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{n}^{\mathrm{2}} −\mathrm{x}^{\mathrm{2}} }{\left(\mathrm{n}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dx}=\mathrm{lim}_{\mathrm{a}\rightarrow\infty} \int_{\mathrm{0}} ^{\mathrm{a}} \frac{\mathrm{n}^{\mathrm{2}} −\mathrm{x}^{\mathrm{2}} }{\left(\mathrm{n}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dx}=\mathrm{lim}_{\mathrm{a}\rightarrow\infty} \frac{\mathrm{a}}{\mathrm{a}^{\mathrm{2}} +\mathrm{n}^{\mathrm{2}} }=\mathrm{0} \\ $$$$\left.\mathrm{3}\right)\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \int_{\mathrm{0}} ^{\infty} \frac{\mathrm{n}^{\mathrm{2}} −\mathrm{x}^{\mathrm{2}} }{\left(\mathrm{n}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dx}=\mathrm{lim}_{\mathrm{k}\rightarrow\infty} \sum_{\mathrm{n}=\mathrm{1}} ^{\mathrm{k}} \int_{\mathrm{0}} ^{\infty} \frac{\mathrm{n}^{\mathrm{2}} −\mathrm{x}^{\mathrm{2}} }{\left(\mathrm{n}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dx}=\mathrm{0} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com