
Question and Answers Forum
Question Number 32737 by caravan msup abdo. last updated on 01/Apr/18
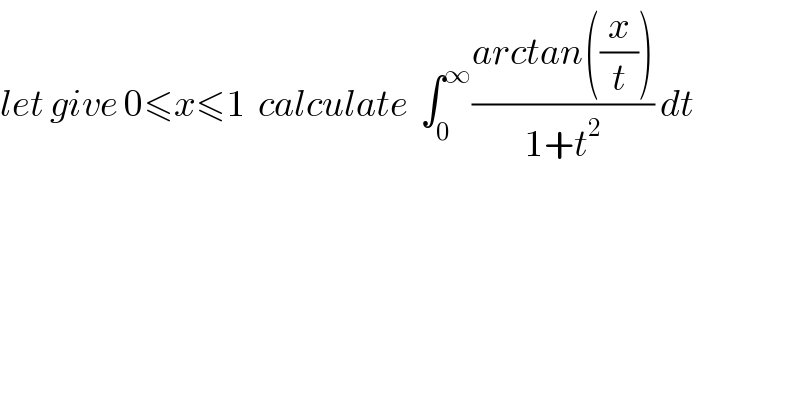
Answered by hknkrc46 last updated on 09/Apr/18

| ||
Question and Answers Forum | ||
Question Number 32737 by caravan msup abdo. last updated on 01/Apr/18 | ||
 | ||
Answered by hknkrc46 last updated on 09/Apr/18 | ||
 | ||
| ||