Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 32897 by artibunja last updated on 06/Apr/18

e^π > π^e or e^π <π^e ?

$$ \\ $$ $${e}^{\pi} \:>\:\pi^{{e}} \:\:{or}\:\:\:{e}^{\pi} <\pi^{{e}} \:? \\ $$ $$ \\ $$

Answered by MJS last updated on 06/Apr/18

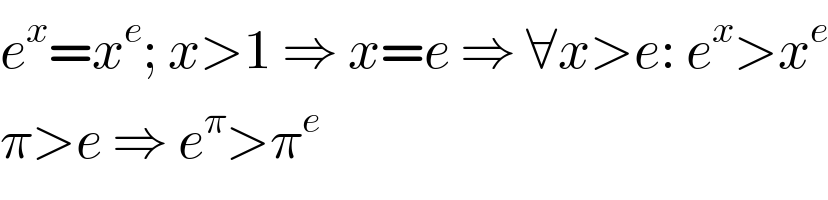
e^x =x^e ; x>1 ⇒ x=e ⇒ ∀x>e: e^x >x^e π>e ⇒ e^π >π^e

$${e}^{{x}} ={x}^{{e}} ;\:{x}>\mathrm{1}\:\Rightarrow\:{x}={e}\:\Rightarrow\:\forall{x}>{e}:\:{e}^{{x}} >{x}^{{e}} \\ $$ $$\pi>{e}\:\Rightarrow\:{e}^{\pi} >\pi^{{e}} \\ $$

Commented byMJS last updated on 06/Apr/18

interestingly for a^x =x^a with a>1 and x>1 two solutions seem to exist (i.e. 2^x =x^2 ⇒ x=2∨x=4; 3^x =x^3 ⇒ x=3∨x≈2.47805) but for a=e there′s only one: x=e can anybody further explain this?

$$\mathrm{interestingly}\:\mathrm{for}\:{a}^{{x}} ={x}^{{a}} \:\mathrm{with}\:{a}>\mathrm{1} \\ $$ $$\mathrm{and}\:{x}>\mathrm{1}\:\mathrm{two}\:\mathrm{solutions}\:\mathrm{seem}\:\mathrm{to} \\ $$ $$\mathrm{exist}\:\left(\mathrm{i}.\mathrm{e}.\:\mathrm{2}^{{x}} ={x}^{\mathrm{2}} \:\Rightarrow\:{x}=\mathrm{2}\vee{x}=\mathrm{4};\right. \\ $$ $$\left.\mathrm{3}^{{x}} ={x}^{\mathrm{3}} \:\Rightarrow\:{x}=\mathrm{3}\vee{x}\approx\mathrm{2}.\mathrm{47805}\right)\:\mathrm{but} \\ $$ $$\mathrm{for}\:{a}={e}\:\mathrm{there}'\mathrm{s}\:\mathrm{only}\:\mathrm{one}:\:{x}={e} \\ $$ $$ \\ $$ $$\mathrm{can}\:\mathrm{anybody}\:\mathrm{further}\:\mathrm{explain}\:\mathrm{this}? \\ $$

Commented bymrW2 last updated on 06/Apr/18

solution for a^x =x^a (a>0): a^(x/a) =x e^((x/a) ln a) =x (−(x/a) ln a) e^(−(x/a) ln a) =−((ln a)/a) ⇒−(x/a) ln a=W(−((ln a)/a)) ⇒x=−(a/(ln a)) W(−((ln a)/a))=−((W(−ln a^(1/a) ))/(ln a^(1/a) )) if a=e: one solution if a≠e: two solutions

$${solution}\:{for}\:{a}^{{x}} ={x}^{{a}} \:\left({a}>\mathrm{0}\right): \\ $$ $${a}^{\frac{{x}}{{a}}} ={x} \\ $$ $${e}^{\frac{{x}}{{a}}\:\mathrm{ln}\:{a}} ={x} \\ $$ $$\left(−\frac{{x}}{{a}}\:\mathrm{ln}\:{a}\right)\:{e}^{−\frac{{x}}{{a}}\:\mathrm{ln}\:{a}} =−\frac{\mathrm{ln}\:{a}}{{a}} \\ $$ $$\Rightarrow−\frac{{x}}{{a}}\:\mathrm{ln}\:{a}={W}\left(−\frac{\mathrm{ln}\:{a}}{{a}}\right) \\ $$ $$\Rightarrow{x}=−\frac{{a}}{\mathrm{ln}\:{a}}\:{W}\left(−\frac{\mathrm{ln}\:{a}}{{a}}\right)=−\frac{{W}\left(−\mathrm{ln}\:{a}^{\frac{\mathrm{1}}{{a}}} \right)}{\mathrm{ln}\:{a}^{\frac{\mathrm{1}}{{a}}} } \\ $$ $${if}\:{a}={e}:\:{one}\:{solution} \\ $$ $${if}\:{a}\neq{e}:\:{two}\:{solutions} \\ $$

Answered by Tinkutara last updated on 06/Apr/18

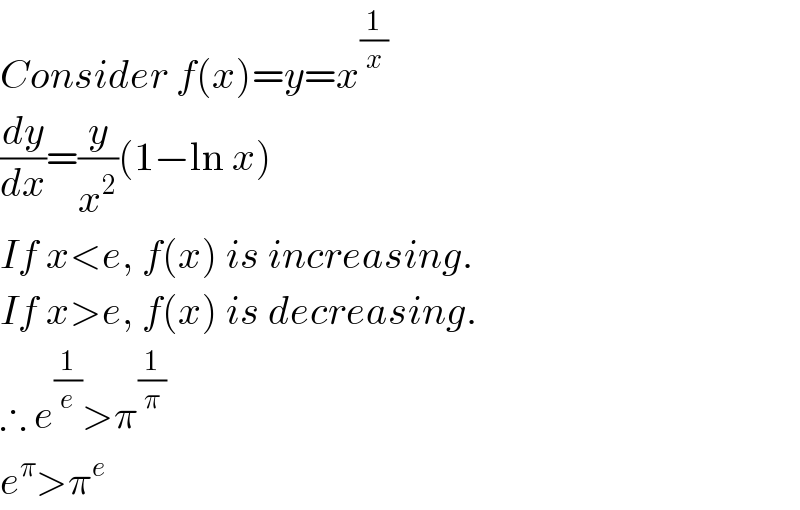
Consider f(x)=y=x^(1/x) (dy/dx)=(y/x^2 )(1−ln x) If x<e, f(x) is increasing. If x>e, f(x) is decreasing. ∴ e^(1/e) >π^(1/π) e^π >π^e

$${Consider}\:{f}\left({x}\right)={y}={x}^{\frac{\mathrm{1}}{{x}}} \\ $$ $$\frac{{dy}}{{dx}}=\frac{{y}}{{x}^{\mathrm{2}} }\left(\mathrm{1}−\mathrm{ln}\:{x}\right) \\ $$ $${If}\:{x}<{e},\:{f}\left({x}\right)\:{is}\:{increasing}. \\ $$ $${If}\:{x}>{e},\:{f}\left({x}\right)\:{is}\:{decreasing}. \\ $$ $$\therefore\:{e}^{\frac{\mathrm{1}}{{e}}} >\pi^{\frac{\mathrm{1}}{\pi}} \\ $$ $${e}^{\pi} >\pi^{{e}} \\ $$

Answered by artibunja last updated on 06/Apr/18

Terms of Service

Privacy Policy

Contact: info@tinkutara.com