
Question and Answers Forum
Question Number 32939 by abdo imad last updated on 06/Apr/18
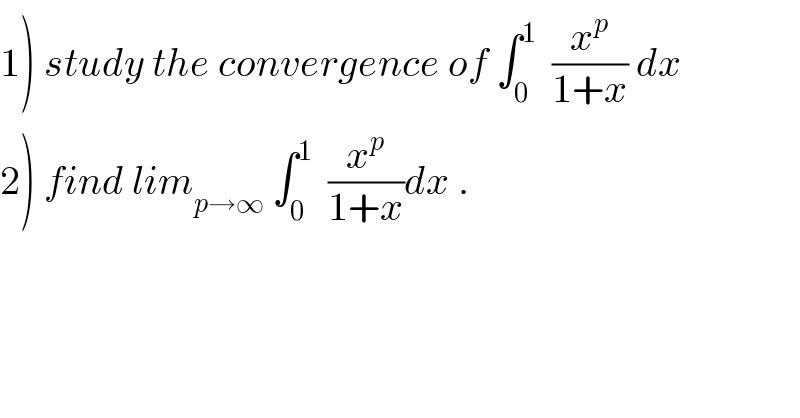
Commented by abdo imad last updated on 08/Apr/18
![let put I =∫_0 ^1 (x^p /(1+x))dx .ch.x=(1/t) give I = ∫_1 ^(+∞) (1/(t^p (1+(1/t)))) (dt/t^2 ) = ∫_1 ^(+∞) (dt/(t^(p+2) +t^(p+1) )) = ∫_1 ^(+∞) (dt/(t^(p+2) ( 1+(1/t)))) .and at V(∞) (1/(t^(p+2) (1+(1/t))))∼ (1/t^(p+2) ) ∫_1 ^(+∞) (dt/t^(p+2) ) converges ⇔ p+2>1 ⇔p >−1 .so I converges ⇔ p>−1 . 2) ∀ x∈[0,1] (x^p /(1+x)) ≤ x^p ⇒ ∫_0 ^1 (x^p /(1+x)) dx ≤ ∫_0 ^1 x^p dx=(1/(p+1)) ⇒ lim_(p→∞) ∫_0 ^1 (x^p /(1+x)) dx =0 .](Q32967.png)
Answered by JDamian last updated on 08/Apr/18
![1) (x^p /(1+x))=x^(p−1) −x^(p−2) + ∙∙∙ (−1)^(p+1) +(((−1)^p )/(x+1))=Σ_(k=0) ^(p−1) (−1)^(p+k+1) x^k ∫_0 ^1 (x^p /(1+x))=[(x^p /p)−(x^(p−1) /(p−1))+ ∙∙∙ +(−1)^(p+1) +(−1)^p ln∣x+1∣]_0 ^1 = =[Σ_(k=1) ^p (−1)^(p+k) (x^k /k) + (−1)^p ln∣x+1∣]_0 ^1 =Σ_(k=1) ^p (((−1)^(p+k) )/k) + (−1)^p ln2= =(1/p)−(1/(p−1))+ ∙∙∙ +(−1)^(p+1) + (−1)^p ln2](Q32964.png)
| ||
Question and Answers Forum | ||
Question Number 32939 by abdo imad last updated on 06/Apr/18 | ||
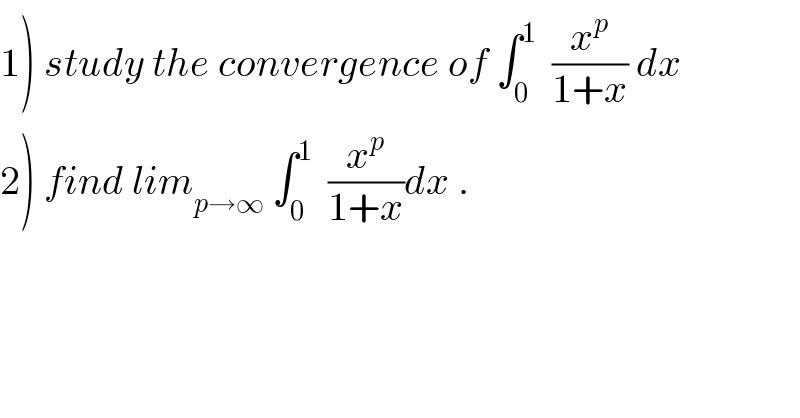 | ||
Commented by abdo imad last updated on 08/Apr/18 | ||
![let put I =∫_0 ^1 (x^p /(1+x))dx .ch.x=(1/t) give I = ∫_1 ^(+∞) (1/(t^p (1+(1/t)))) (dt/t^2 ) = ∫_1 ^(+∞) (dt/(t^(p+2) +t^(p+1) )) = ∫_1 ^(+∞) (dt/(t^(p+2) ( 1+(1/t)))) .and at V(∞) (1/(t^(p+2) (1+(1/t))))∼ (1/t^(p+2) ) ∫_1 ^(+∞) (dt/t^(p+2) ) converges ⇔ p+2>1 ⇔p >−1 .so I converges ⇔ p>−1 . 2) ∀ x∈[0,1] (x^p /(1+x)) ≤ x^p ⇒ ∫_0 ^1 (x^p /(1+x)) dx ≤ ∫_0 ^1 x^p dx=(1/(p+1)) ⇒ lim_(p→∞) ∫_0 ^1 (x^p /(1+x)) dx =0 .](Q32967.png) | ||
Answered by JDamian last updated on 08/Apr/18 | ||
![1) (x^p /(1+x))=x^(p−1) −x^(p−2) + ∙∙∙ (−1)^(p+1) +(((−1)^p )/(x+1))=Σ_(k=0) ^(p−1) (−1)^(p+k+1) x^k ∫_0 ^1 (x^p /(1+x))=[(x^p /p)−(x^(p−1) /(p−1))+ ∙∙∙ +(−1)^(p+1) +(−1)^p ln∣x+1∣]_0 ^1 = =[Σ_(k=1) ^p (−1)^(p+k) (x^k /k) + (−1)^p ln∣x+1∣]_0 ^1 =Σ_(k=1) ^p (((−1)^(p+k) )/k) + (−1)^p ln2= =(1/p)−(1/(p−1))+ ∙∙∙ +(−1)^(p+1) + (−1)^p ln2](Q32964.png) | ||
| ||