Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 32951 by math1967 last updated on 07/Apr/18

Evaluate ∫((x^4 +1)/(x^6 +1))dx [W.B.H.S 2018]

$${Evaluate} \\ $$$$\int\frac{{x}^{\mathrm{4}} +\mathrm{1}}{{x}^{\mathrm{6}} +\mathrm{1}}{dx}\:\:\:\:\:\left[{W}.{B}.{H}.{S}\:\mathrm{2018}\right] \\ $$

Commented by abdo imad last updated on 09/Apr/18

yes i have commited a error becaus i don t give attention to limits(bornes) thank for this remark... i have deleted the post..

$${yes}\:{i}\:{have}\:{commited}\:{a}\:{error}\:\:{becaus}\:{i}\:{don}\:{t}\:{give}\: \\ $$$${attention}\:{to}\:{limits}\left({bornes}\right)\:{thank}\:{for}\:{this}\:{remark}... \\ $$$${i}\:{have}\:{deleted}\:{the}\:{post}.. \\ $$

Answered by Joel578 last updated on 07/Apr/18

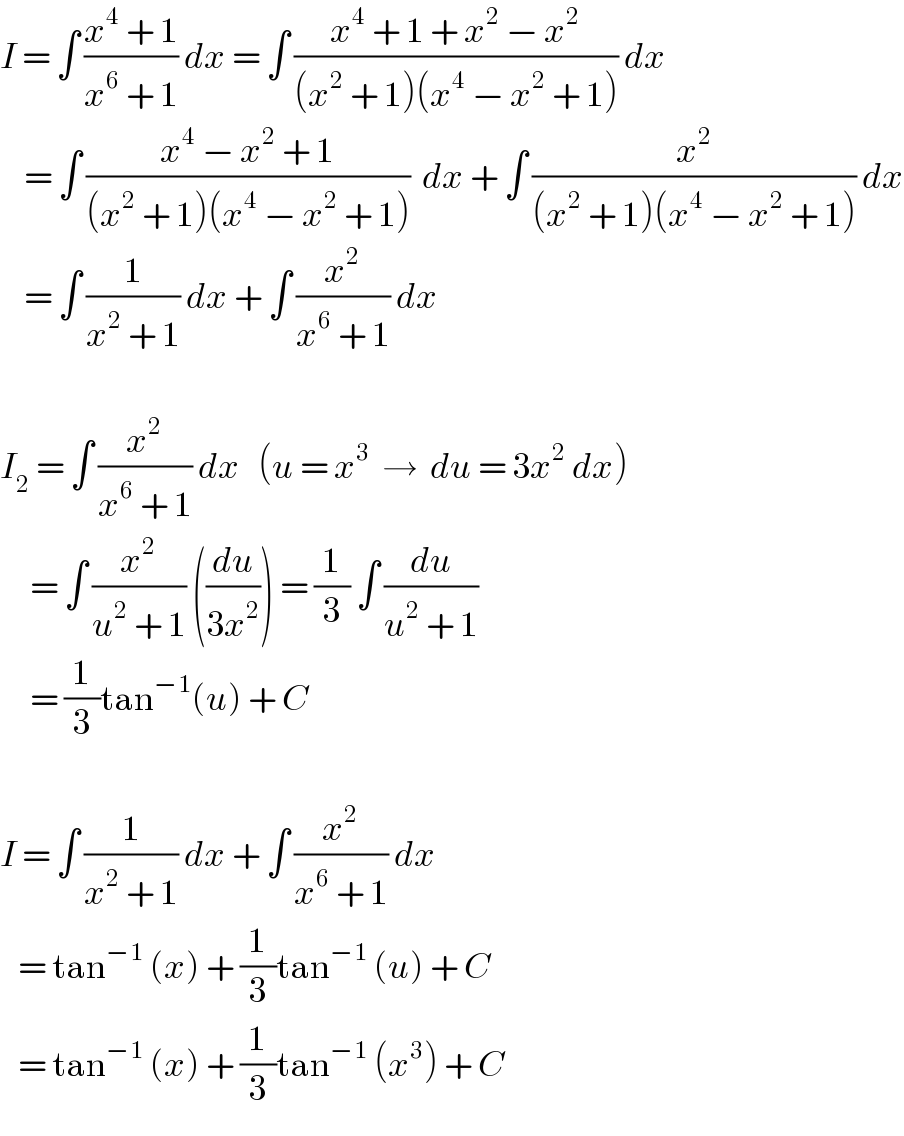
I = ∫ ((x^4 + 1)/(x^6 + 1)) dx = ∫ ((x^4 + 1 + x^2 − x^2 )/((x^2 + 1)(x^4 − x^2 + 1))) dx = ∫ ((x^4 − x^2 + 1)/((x^2 + 1)(x^4 − x^2 + 1))) dx + ∫ (x^2 /((x^2 + 1)(x^4 − x^2 + 1))) dx = ∫ (1/(x^2 + 1)) dx + ∫ (x^2 /(x^6 + 1)) dx I_2 = ∫ (x^2 /(x^6 + 1)) dx (u = x^3 → du = 3x^2 dx) = ∫ (x^2 /(u^2 + 1)) ((du/(3x^2 ))) = (1/3) ∫ (du/(u^2 + 1)) = (1/3)tan^(−1) (u) + C I = ∫ (1/(x^2 + 1)) dx + ∫ (x^2 /(x^6 + 1)) dx = tan^(−1) (x) + (1/3)tan^(−1) (u) + C = tan^(−1) (x) + (1/3)tan^(−1) (x^3 ) + C

$${I}\:=\:\int\:\frac{{x}^{\mathrm{4}} \:+\:\mathrm{1}}{{x}^{\mathrm{6}} \:+\:\mathrm{1}}\:{dx}\:=\:\int\:\frac{{x}^{\mathrm{4}} \:+\:\mathrm{1}\:+\:{x}^{\mathrm{2}} \:−\:{x}^{\mathrm{2}} }{\left({x}^{\mathrm{2}} \:+\:\mathrm{1}\right)\left({x}^{\mathrm{4}} \:−\:{x}^{\mathrm{2}} \:+\:\mathrm{1}\right)}\:{dx} \\ $$$$\:\:\:\:=\:\int\:\frac{{x}^{\mathrm{4}} \:−\:{x}^{\mathrm{2}} \:+\:\mathrm{1}}{\left({x}^{\mathrm{2}} \:+\:\mathrm{1}\right)\left({x}^{\mathrm{4}} \:−\:{x}^{\mathrm{2}} \:+\:\mathrm{1}\right)}\:\:{dx}\:+\:\int\:\frac{{x}^{\mathrm{2}} }{\left({x}^{\mathrm{2}} \:+\:\mathrm{1}\right)\left({x}^{\mathrm{4}} \:−\:{x}^{\mathrm{2}} \:+\:\mathrm{1}\right)}\:{dx} \\ $$$$\:\:\:\:=\:\int\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} \:+\:\mathrm{1}}\:{dx}\:+\:\int\:\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{6}} \:+\:\mathrm{1}}\:{dx} \\ $$$$\: \\ $$$${I}_{\mathrm{2}} \:=\:\int\:\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{6}} \:+\:\mathrm{1}}\:{dx}\:\:\:\left({u}\:=\:{x}^{\mathrm{3}} \:\:\rightarrow\:\:{du}\:=\:\mathrm{3}{x}^{\mathrm{2}} \:{dx}\right) \\ $$$$\:\:\:\:\:=\:\int\:\frac{{x}^{\mathrm{2}} }{{u}^{\mathrm{2}} \:+\:\mathrm{1}}\:\left(\frac{{du}}{\mathrm{3}{x}^{\mathrm{2}} }\right)\:=\:\frac{\mathrm{1}}{\mathrm{3}}\:\int\:\frac{{du}}{{u}^{\mathrm{2}} \:+\:\mathrm{1}} \\ $$$$\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{3}}\mathrm{tan}^{−\mathrm{1}} \left({u}\right)\:+\:{C} \\ $$$$ \\ $$$${I}\:=\:\int\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} \:+\:\mathrm{1}}\:{dx}\:+\:\int\:\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{6}} \:+\:\mathrm{1}}\:{dx} \\ $$$$\:\:\:=\:\mathrm{tan}^{−\mathrm{1}} \:\left({x}\right)\:+\:\frac{\mathrm{1}}{\mathrm{3}}\mathrm{tan}^{−\mathrm{1}} \:\left({u}\right)\:+\:{C} \\ $$$$\:\:\:=\:\mathrm{tan}^{−\mathrm{1}} \:\left({x}\right)\:+\:\frac{\mathrm{1}}{\mathrm{3}}\mathrm{tan}^{−\mathrm{1}} \:\left({x}^{\mathrm{3}} \right)\:+\:{C} \\ $$

Answered by MJS last updated on 07/Apr/18

lol! I did it the hard way... x^6 +1=(x^4 −x^2 +1)(x^2 +1)= =(x^2 −(√3)x+1)(x^2 +(√3)x+1)(x^2 +1) ((x^4 +1)/(x^6 +1))=(N_1 /(x^2 −(√3)x+1))+(N_2 /(x^2 +(√3)+1))+(N_3 /(x^2 +1 )) N_1 =N_2 =(1/6); N_3 =(2/3) ∫((x^4 +1)/(x^6 +1))dx=∫(1/(6(x^2 −(√3)x+1)))dx+∫(1/(6(x^2 +(√3)x+1)))dx+∫(2/(3(x^2 +1)))dx= [∫(1/(ax^2 +bx+c))dx=(2/(√(−b^2 +4ac)))tan^(−1) ((2ax+b)/(√(−b^2 +4ac))); b^2 −4ac<0] =(1/3)(tan^(−1) (2x−(√3))+tan^(−1) (2x+(√3))+2tan^(−1) (x))+C

$$\mathrm{lol}!\:\mathrm{I}\:\mathrm{did}\:\mathrm{it}\:\mathrm{the}\:\mathrm{hard}\:\mathrm{way}... \\ $$$${x}^{\mathrm{6}} +\mathrm{1}=\left({x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{1}\right)= \\ $$$$=\left({x}^{\mathrm{2}} −\sqrt{\mathrm{3}}{x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} +\sqrt{\mathrm{3}}{x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$\frac{{x}^{\mathrm{4}} +\mathrm{1}}{{x}^{\mathrm{6}} +\mathrm{1}}=\frac{{N}_{\mathrm{1}} }{{x}^{\mathrm{2}} −\sqrt{\mathrm{3}}{x}+\mathrm{1}}+\frac{{N}_{\mathrm{2}} }{{x}^{\mathrm{2}} +\sqrt{\mathrm{3}}+\mathrm{1}}+\frac{{N}_{\mathrm{3}} }{{x}^{\mathrm{2}} +\mathrm{1}\:} \\ $$$${N}_{\mathrm{1}} ={N}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{6}};\:{N}_{\mathrm{3}} =\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\int\frac{{x}^{\mathrm{4}} +\mathrm{1}}{{x}^{\mathrm{6}} +\mathrm{1}}{dx}=\int\frac{\mathrm{1}}{\mathrm{6}\left({x}^{\mathrm{2}} −\sqrt{\mathrm{3}}{x}+\mathrm{1}\right)}{dx}+\int\frac{\mathrm{1}}{\mathrm{6}\left({x}^{\mathrm{2}} +\sqrt{\mathrm{3}}{x}+\mathrm{1}\right)}{dx}+\int\frac{\mathrm{2}}{\mathrm{3}\left({x}^{\mathrm{2}} +\mathrm{1}\right)}{dx}= \\ $$$$\:\:\:\:\:\left[\int\frac{\mathrm{1}}{{ax}^{\mathrm{2}} +{bx}+{c}}{dx}=\frac{\mathrm{2}}{\sqrt{−{b}^{\mathrm{2}} +\mathrm{4}{ac}}}\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{2}{ax}+{b}}{\sqrt{−{b}^{\mathrm{2}} +\mathrm{4}{ac}}};\:{b}^{\mathrm{2}} −\mathrm{4}{ac}<\mathrm{0}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2}{x}−\sqrt{\mathrm{3}}\right)+\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2}{x}+\sqrt{\mathrm{3}}\right)+\mathrm{2tan}^{−\mathrm{1}} \left({x}\right)\right)+{C} \\ $$

Commented by Joel578 last updated on 08/Apr/18

Great work Sir

$$\mathrm{Great}\:\mathrm{work}\:\mathrm{Sir} \\ $$

Commented by MJS last updated on 08/Apr/18

thanks, but I like your solution more than mine

$$\mathrm{thanks},\:\mathrm{but}\:\mathrm{I}\:\mathrm{like}\:\mathrm{your}\:\mathrm{solution} \\ $$$$\mathrm{more}\:\mathrm{than}\:\mathrm{mine} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com