
Question Number 3296 by prakash jain last updated on 09/Dec/15

$$\mathrm{If}\:{n},{p},{q}\in\mathbb{Z}^{+} \:\mathrm{and}\:{p}\:\mathrm{and}\:{q}\:\mathrm{are}\:\mathrm{coprimes}, \\ $$ $$\mathrm{then}\:\mathrm{prove}\:\mathrm{that}\:\mathrm{HCF}\:\mathrm{of}\:\left({n}^{{p}} −\mathrm{1}\right)\:\mathrm{and}\:\left({n}^{{q}} −\mathrm{1}\right)\:\mathrm{is}\:\left({n}−\mathrm{1}\right). \\ $$ $$\mathrm{Assume}\:{n}>\mathrm{1}. \\ $$
Commented byRasheed Soomro last updated on 10/Dec/15
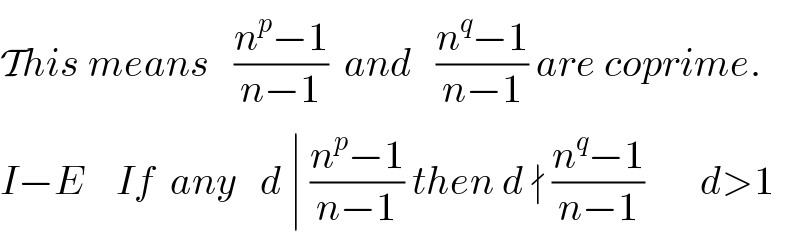
$$\mathcal{T}{his}\:{means}\:\:\:\frac{{n}^{{p}} −\mathrm{1}}{{n}−\mathrm{1}}\:\:{and}\:\:\:\frac{{n}^{{q}} −\mathrm{1}}{{n}−\mathrm{1}}\:{are}\:{coprime}. \\ $$ $${I}−{E}\:\:\:\:{If}\:\:{any}\:\:\:{d}\:\mid\:\frac{{n}^{{p}} −\mathrm{1}}{{n}−\mathrm{1}}\:{then}\:{d}\:\nmid\:\frac{{n}^{{q}} −\mathrm{1}}{{n}−\mathrm{1}}\:\:\:\:\:\:\:{d}>\mathrm{1} \\ $$
Commented byprakash jain last updated on 10/Dec/15

$$\mathrm{Yes}. \\ $$
Commented byRasheed Soomro last updated on 10/Dec/15

$$\mathcal{E}{asily}\:{can}\:{be}\:{shown}\:{that} \\ $$ $$\left({n}−\mathrm{1}\right)\mid\:\left({n}^{{p}} −\mathrm{1}\right)\:\:\:\wedge\:\:\:\left({n}−\mathrm{1}\right)\mid\:\left({n}^{{q}} −\mathrm{1}\right) \\ $$ $${i}\:{e}\:{n}−\mathrm{1}\:{is}\:{a}\:{common}\:{divisor}. \\ $$ $$\mathcal{N}{ow}\:{we}\:{have}\:{to}\:{prove}\:{that}\:{any}\:{number}\:{greater}\:{than} \\ $$ $${n}−\mathrm{1}\:{can}'{t}\:{divide}\:{both}. \\ $$ $${Let}\:{k}\:>\:\mathrm{0}\:\:{and}\:{k}\in\mathbb{N}\:\Rightarrow{n}+{k}−\mathrm{1}>{n}−\mathrm{1} \\ $$ $${We}\:{have}\:{to}\:{prove}: \\ $$ $$\:\:\:\:\:\:{n}^{{p}} −\mathrm{1}\ncong\mathrm{0}\:\left({mod}\:{n}+{k}−\mathrm{1}\right)\:\wedge\:{n}^{{p}} −\mathrm{1}\ncong\mathrm{0}\:\left({mod}\:{n}+{k}−\mathrm{1}\right) \\ $$ $$\because\:{k}\in\:\mathbb{N}\:\:\:{therfore}\:{perhsps}\:{mathematical}\:{induction}\: \\ $$ $${could}\:{help}. \\ $$
Answered by prakash jain last updated on 11/Dec/15
![After removing common factor (n−1). A=Σ_(j=1) ^p n^(j−1) , B=Σ_(j=1) ^q n^(j−1) Let us say d>1 is common factor in A and B. clearly d ∤ n since in that (A/d)∈N will imply (1/d)∈N. let us assume p>q. since d divides B=Σ_(j=1) ^q n^(j−1) there exists k≤q such that d divides Σ_(j=1) ^k n^(j−1) , let us smallest value of k for which d divides Σ_(j=1) ^k n^(j−1) is i. Clearly i>1. if q=mi+r, r<i B=Σ_(j=1) ^(mi+r) n^(j−1) =Σ_(x=0) ^(m−1) n^(xi) [Σ_(j=1) ^i n^(j−1) ]+n^(mi) Σ_(j=1) ^r n^(j−1) if d divides B then d divides n^(mi) Σ_(j=1) ^r n^(j−1) since d∤n^(mi) ⇒ d divides Σ_(j=1) ^r n^(j−1) Sincd r<i, it contradicts that i is the smallest value for k where Σ_(j=1) ^k n^(j−1) is divisible by d. So r must be equal to 0. ⇒q=mi similarly p=ki So i>1 is common factor between q and p. contradicts p and q are coprime. hence no common factor between A and B.](Q3327.png)
$$\mathrm{After}\:\mathrm{removing}\:\mathrm{common}\:\mathrm{factor}\:\left({n}−\mathrm{1}\right). \\ $$ $${A}=\underset{{j}=\mathrm{1}} {\overset{{p}} {\sum}}{n}^{{j}−\mathrm{1}} ,\:{B}=\underset{{j}=\mathrm{1}} {\overset{{q}} {\sum}}{n}^{{j}−\mathrm{1}} \\ $$ $$\mathrm{Let}\:\mathrm{us}\:\mathrm{say}\:{d}>\mathrm{1}\:\mathrm{is}\:\mathrm{common}\:\mathrm{factor}\:\mathrm{in}\:{A}\:{and}\:{B}. \\ $$ $$\mathrm{clearly}\:{d}\:\nmid\:{n}\:\mathrm{since}\:\mathrm{in}\:\mathrm{that}\:\frac{{A}}{{d}}\in\mathbb{N}\:\mathrm{will}\:\mathrm{imply} \\ $$ $$\frac{\mathrm{1}}{{d}}\in\mathbb{N}. \\ $$ $$ \\ $$ $${let}\:{us}\:{assume}\:{p}>{q}. \\ $$ $${since}\:{d}\:\mathrm{divides}\:{B}=\underset{{j}=\mathrm{1}} {\overset{{q}} {\sum}}{n}^{{j}−\mathrm{1}} \:\mathrm{there}\:\mathrm{exists}\:{k}\leqslant{q} \\ $$ $$\mathrm{such}\:\mathrm{that}\:{d}\:\mathrm{divides}\:\underset{{j}=\mathrm{1}} {\overset{{k}} {\sum}}{n}^{{j}−\mathrm{1}} ,\:\mathrm{let}\:\mathrm{us}\:\mathrm{smallest} \\ $$ $$\mathrm{value}\:\mathrm{of}\:{k}\:\mathrm{for}\:\mathrm{which}\:{d}\:\mathrm{divides}\:\underset{{j}=\mathrm{1}} {\overset{{k}} {\sum}}{n}^{{j}−\mathrm{1}} \:\mathrm{is}\:{i}. \\ $$ $$\mathrm{Clearly}\:{i}>\mathrm{1}. \\ $$ $$ \\ $$ $${if}\:{q}={mi}+{r},\:{r}<{i} \\ $$ $${B}=\underset{{j}=\mathrm{1}} {\overset{{mi}+{r}} {\sum}}{n}^{{j}−\mathrm{1}} =\underset{{x}=\mathrm{0}} {\overset{{m}−\mathrm{1}} {\sum}}{n}^{{xi}} \:\left[\underset{{j}=\mathrm{1}} {\overset{{i}} {\sum}}{n}^{{j}−\mathrm{1}} \right]+{n}^{{mi}} \underset{{j}=\mathrm{1}} {\overset{{r}} {\sum}}{n}^{{j}−\mathrm{1}} \\ $$ $${if}\:{d}\:{divides}\:{B}\:\mathrm{then}\:{d}\:{divides}\:{n}^{{mi}} \underset{{j}=\mathrm{1}} {\overset{{r}} {\sum}}{n}^{{j}−\mathrm{1}} \:{since} \\ $$ $${d}\nmid{n}^{{mi}} \:\Rightarrow\:{d}\:{divides}\:\underset{{j}=\mathrm{1}} {\overset{{r}} {\sum}}{n}^{{j}−\mathrm{1}} \: \\ $$ $$ \\ $$ $$\mathrm{Sincd}\:{r}<{i},\:\mathrm{it}\:\mathrm{contradicts}\:\:\mathrm{that} \\ $$ $${i}\:\mathrm{is}\:\mathrm{the}\:\mathrm{smallest}\:\mathrm{value}\:\mathrm{for}\:{k}\:\:\mathrm{where}\:\underset{{j}=\mathrm{1}} {\overset{{k}} {\sum}}{n}^{{j}−\mathrm{1}} \\ $$ $$\mathrm{is}\:\mathrm{divisible}\:\mathrm{by}\:{d}.\:\mathrm{So}\:{r}\:\mathrm{must}\:\mathrm{be}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{0}. \\ $$ $$\Rightarrow{q}={mi} \\ $$ $$ \\ $$ $${similarly}\:{p}={ki} \\ $$ $$\mathrm{So}\:{i}>\mathrm{1}\:\mathrm{is}\:\mathrm{common}\:\mathrm{factor}\:\mathrm{between}\:{q}\:\mathrm{and}\:{p}. \\ $$ $${contradicts}\:{p}\:{and}\:{q}\:\mathrm{are}\:\mathrm{coprime}. \\ $$ $$\mathrm{hence}\:\mathrm{no}\:\mathrm{common}\:\mathrm{factor}\:\mathrm{between}\:{A}\:\mathrm{and}\:{B}. \\ $$
