Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 33009 by kyle_TW last updated on 09/Apr/18

help ! ! ! ∫ (dx/(csc(x)−1)) = ? [ my way ] ∫( (dx/((1/(sinx)) − 1)) ) =∫((sinx)/(1−sinx)) dx =−∫ ((sinx−1+1)/(sinx−1)) dx =−∫1+(1/(sinx−1)) dx =−(∫1dx+∫((sinx+1)/((sinx−1)(sinx+1))) dx) =−(x+C−∫((sinx+1)/(1−sin^2 x)) dx) =−(x+C−∫ ((sinx)/(cos^2 x)) dx−∫ (1/(cos^2 x)) dx) =−(x+C+∫(cosx)^(−2) dcosx−∫(1/(cos^2 x))dx) =−(x−(cosx)^(−1) +C−∫(1/(cos^2 x))dx) ...and I can′t solve the ∫(1/(cos^2 x))dx oh i just found that is tanx+C

$${help}\:!\:!\:! \\ $$$$\int\:\frac{{dx}}{{csc}\left({x}\right)−\mathrm{1}}\:=\:? \\ $$$$ \\ $$$$\left[\:{my}\:{way}\:\right] \\ $$$$\int\left(\:\frac{{dx}}{\frac{\mathrm{1}}{{sinx}}\:−\:\mathrm{1}}\:\right) \\ $$$$=\int\frac{{sinx}}{\mathrm{1}−{sinx}}\:{dx} \\ $$$$=−\int\:\frac{{sinx}−\mathrm{1}+\mathrm{1}}{{sinx}−\mathrm{1}}\:{dx} \\ $$$$=−\int\mathrm{1}+\frac{\mathrm{1}}{{sinx}−\mathrm{1}}\:{dx} \\ $$$$=−\left(\int\mathrm{1}{dx}+\int\frac{{sinx}+\mathrm{1}}{\left({sinx}−\mathrm{1}\right)\left({sinx}+\mathrm{1}\right)}\:{dx}\right) \\ $$$$=−\left({x}+{C}−\int\frac{{sinx}+\mathrm{1}}{\mathrm{1}−{sin}^{\mathrm{2}} {x}}\:{dx}\right) \\ $$$$=−\left({x}+{C}−\int\:\frac{{sinx}}{{cos}^{\mathrm{2}} {x}}\:{dx}−\int\:\frac{\mathrm{1}}{{cos}^{\mathrm{2}} {x}}\:{dx}\right) \\ $$$$=−\left({x}+{C}+\int\left({cosx}\right)^{−\mathrm{2}} {dcosx}−\int\frac{\mathrm{1}}{{cos}^{\mathrm{2}} {x}}{dx}\right) \\ $$$$=−\left({x}−\left({cosx}\right)^{−\mathrm{1}} +{C}−\int\frac{\mathrm{1}}{{cos}^{\mathrm{2}} {x}}{dx}\right) \\ $$$$...{and}\:{I}\:{can}'{t}\:{solve}\:{the}\:\int\frac{\mathrm{1}}{{cos}^{\mathrm{2}} {x}}{dx} \\ $$$$ \\ $$$${oh}\:{i}\:{just}\:{found}\:{that}\:{is}\:{tanx}+{C} \\ $$

Commented by prof Abdo imad last updated on 09/Apr/18

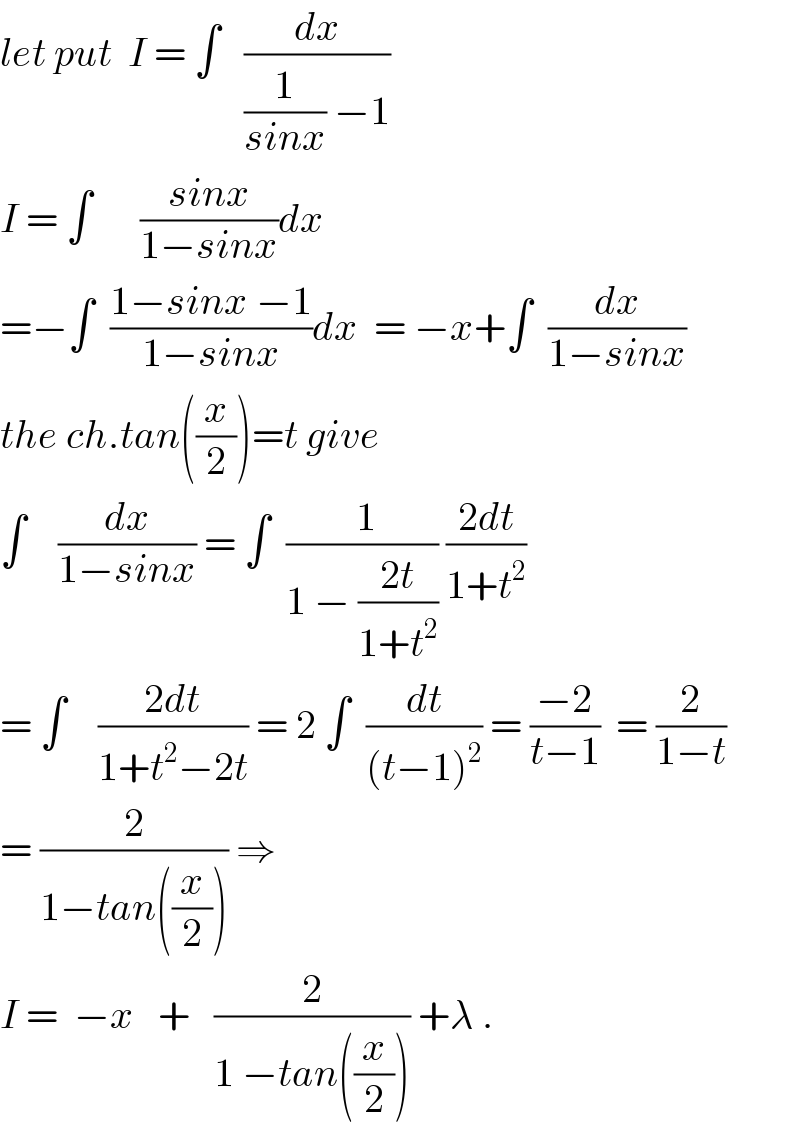
let put I = ∫ (dx/((1/(sinx)) −1)) I = ∫ ((sinx)/(1−sinx))dx =−∫ ((1−sinx −1)/(1−sinx))dx = −x+∫ (dx/(1−sinx)) the ch.tan((x/2))=t give ∫ (dx/(1−sinx)) = ∫ (( 1)/(1 − ((2t)/(1+t^2 )))) ((2dt)/(1+t^2 )) = ∫ ((2dt)/(1+t^2 −2t)) = 2 ∫ (dt/((t−1)^2 )) = ((−2)/(t−1)) = (2/(1−t)) = (2/(1−tan((x/2)))) ⇒ I = −x + (2/(1 −tan((x/2)))) +λ .

$${let}\:{put}\:\:{I}\:=\:\int\:\:\:\frac{{dx}}{\frac{\mathrm{1}}{{sinx}}\:−\mathrm{1}} \\ $$$${I}\:=\:\int\:\:\:\:\:\:\frac{{sinx}}{\mathrm{1}−{sinx}}{dx}\: \\ $$$$=−\int\:\:\frac{\mathrm{1}−{sinx}\:−\mathrm{1}}{\mathrm{1}−{sinx}}{dx}\:\:=\:−{x}+\int\:\:\frac{{dx}}{\mathrm{1}−{sinx}} \\ $$$${the}\:{ch}.{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}\:{give} \\ $$$$\int\:\:\:\:\frac{{dx}}{\mathrm{1}−{sinx}}\:=\:\int\:\:\frac{\:\mathrm{1}}{\mathrm{1}\:−\:\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }}\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$=\:\int\:\:\:\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} −\mathrm{2}{t}}\:=\:\mathrm{2}\:\int\:\:\frac{{dt}}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} }\:=\:\frac{−\mathrm{2}}{{t}−\mathrm{1}}\:\:=\:\frac{\mathrm{2}}{\mathrm{1}−{t}} \\ $$$$=\:\frac{\mathrm{2}}{\mathrm{1}−{tan}\left(\frac{{x}}{\mathrm{2}}\right)}\:\Rightarrow \\ $$$${I}\:=\:\:−{x}\:\:\:+\:\:\:\frac{\mathrm{2}}{\mathrm{1}\:−{tan}\left(\frac{{x}}{\mathrm{2}}\right)}\:+\lambda\:. \\ $$

Answered by Joel578 last updated on 09/Apr/18

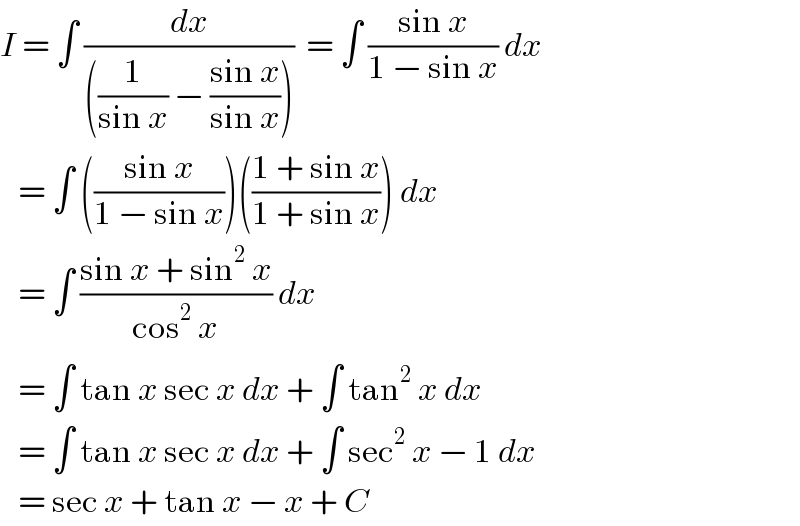
I = ∫ (dx/(((1/(sin x)) − ((sin x)/(sin x))))) = ∫ ((sin x)/(1 − sin x)) dx = ∫ (((sin x)/(1 − sin x)))(((1 + sin x)/(1 + sin x))) dx = ∫ ((sin x + sin^2 x)/(cos^2 x)) dx = ∫ tan x sec x dx + ∫ tan^2 x dx = ∫ tan x sec x dx + ∫ sec^2 x − 1 dx = sec x + tan x − x + C

$${I}\:=\:\int\:\frac{{dx}}{\left(\frac{\mathrm{1}}{\mathrm{sin}\:{x}}\:−\:\frac{\mathrm{sin}\:{x}}{\mathrm{sin}\:{x}}\right)}\:\:=\:\int\:\frac{\mathrm{sin}\:{x}}{\mathrm{1}\:−\:\mathrm{sin}\:{x}}\:{dx} \\ $$$$\:\:\:=\:\int\:\left(\frac{\mathrm{sin}\:{x}}{\mathrm{1}\:−\:\mathrm{sin}\:{x}}\right)\left(\frac{\mathrm{1}\:+\:\mathrm{sin}\:{x}}{\mathrm{1}\:+\:\mathrm{sin}\:{x}}\right)\:{dx} \\ $$$$\:\:\:=\:\int\:\frac{\mathrm{sin}\:{x}\:+\:\mathrm{sin}^{\mathrm{2}} \:{x}}{\mathrm{cos}^{\mathrm{2}} \:{x}}\:{dx} \\ $$$$\:\:\:=\:\int\:\mathrm{tan}\:{x}\:\mathrm{sec}\:{x}\:{dx}\:+\:\int\:\mathrm{tan}^{\mathrm{2}} \:{x}\:{dx} \\ $$$$\:\:\:=\:\int\:\mathrm{tan}\:{x}\:\mathrm{sec}\:{x}\:{dx}\:+\:\int\:\mathrm{sec}^{\mathrm{2}} \:{x}\:−\:\mathrm{1}\:{dx} \\ $$$$\:\:\:=\:\mathrm{sec}\:{x}\:+\:\mathrm{tan}\:{x}\:−\:{x}\:+\:{C} \\ $$

Commented by kyle_TW last updated on 09/Apr/18

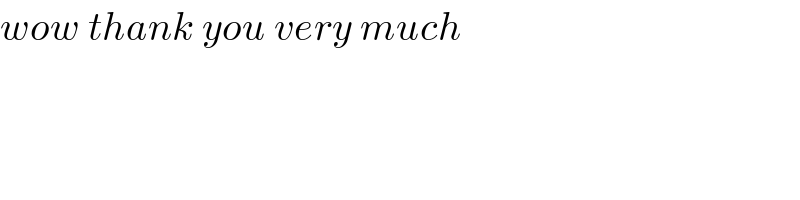
wow thank you very much

$${wow}\:{thank}\:{you}\:{very}\:{much} \\ $$

Commented by kyle_TW last updated on 09/Apr/18

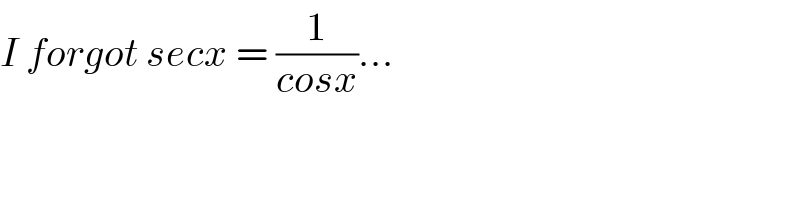
I forgot secx = (1/(cosx))...

$${I}\:{forgot}\:{secx}\:=\:\frac{\mathrm{1}}{{cosx}}... \\ $$

Answered by math1967 last updated on 09/Apr/18

∫(1/(cosex−1))dx ∫((cosex+1)/(cot^2 x))dx ∫((cosecx)/(cot^2 x))dx +∫tan^2 xdx ∫((sinx)/(cos^2 x))dx +∫sec^2 x −∫dx −∫((d(cosx))/(cos^2 x)) +tanx −x (1/3)×(1/(cos^3 x)) +tanx −x +C

$$\int\frac{\mathrm{1}}{{cosex}−\mathrm{1}}{dx} \\ $$$$\int\frac{{cosex}+\mathrm{1}}{{cot}^{\mathrm{2}} {x}}{dx} \\ $$$$\int\frac{{cosecx}}{{cot}^{\mathrm{2}} {x}}{dx}\:+\int{tan}^{\mathrm{2}} {xdx} \\ $$$$\int\frac{{sinx}}{{cos}^{\mathrm{2}} {x}}{dx}\:+\int{sec}^{\mathrm{2}} {x}\:−\int{dx} \\ $$$$−\int\frac{{d}\left({cosx}\right)}{{cos}^{\mathrm{2}} {x}}\:+{tanx}\:−{x} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{1}}{{cos}^{\mathrm{3}} {x}}\:+{tanx}\:−{x}\:+{C} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com