
Question and Answers Forum
Question Number 33026 by prof Abdo imad last updated on 09/Apr/18
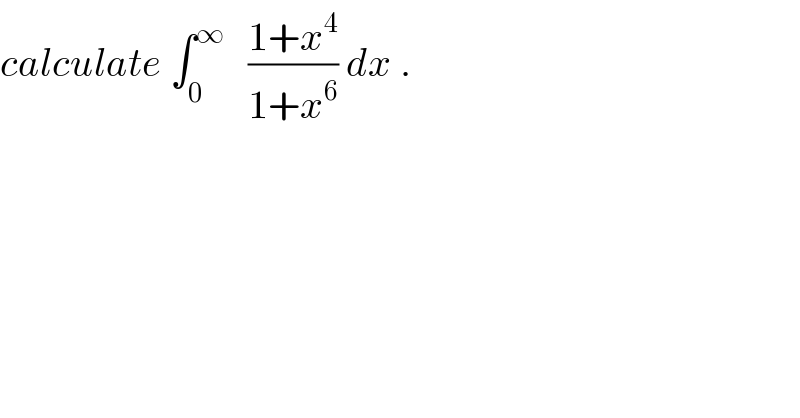
Commented by abdo imad last updated on 09/Apr/18
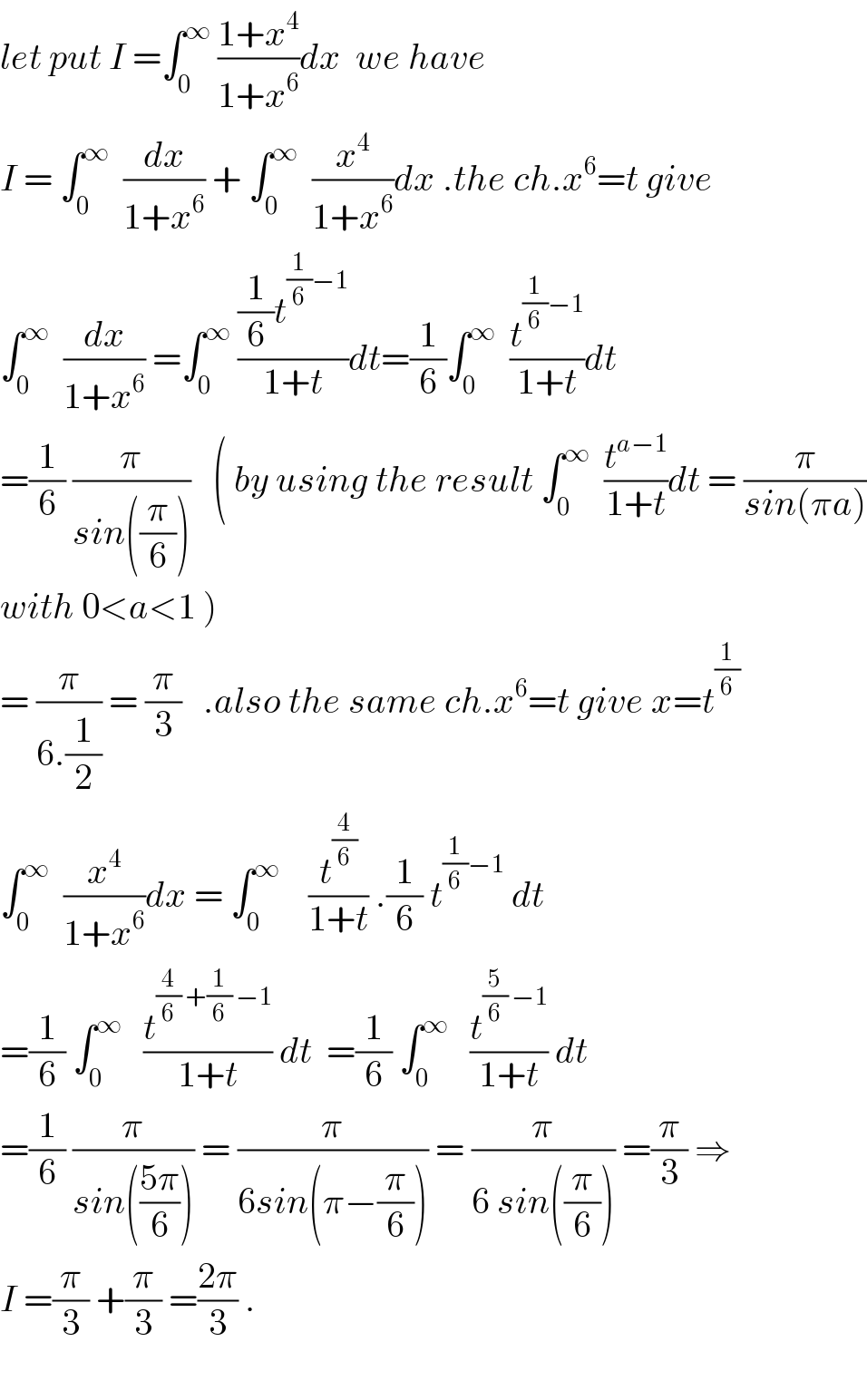
Answered by Joel578 last updated on 09/Apr/18
![I = lim_(n→∞) (∫_0 ^n ((x^4 + 1)/(x^6 + 1)) dx) ∫ ((x^4 + 1)/(x^6 + 1)) dx = ∫ ((x^4 + 1 + x^2 − x^2 )/((x^2 +1)(x^4 − x^2 + 1))) dx = ∫ (1/(x^2 + 1)) dx + ∫ (x^2 /(x^6 + 1)) dx = tan^(−1) x + ∫ (x^2 /(x^6 + 1)) dx (u = x^3 → du = 3x^2 dx) = tan^(−1) x + (1/3) ∫ (1/(u^2 + 1)) du = tan^(−1) x + (1/3)tan^(−1) u + C = tan^(−1) (x) + (1/3)tan^(−1) (x^3 ) + C I = lim_(n→∞) [tan^(−1) (x) + (1/3)tan^(−1) (x^3 )]_0 ^n = lim_(n→∞) (tan^(−1) (n) + (1/3)tan^(−1) (n^3 )) − (tan^(−1) (0) + (1/3)tan^(−1) (0)) = (π/2) + (1/3)((π/2)) − 0 = ((2π)/3)](Q33030.png)
| ||
Question and Answers Forum | ||
Question Number 33026 by prof Abdo imad last updated on 09/Apr/18 | ||
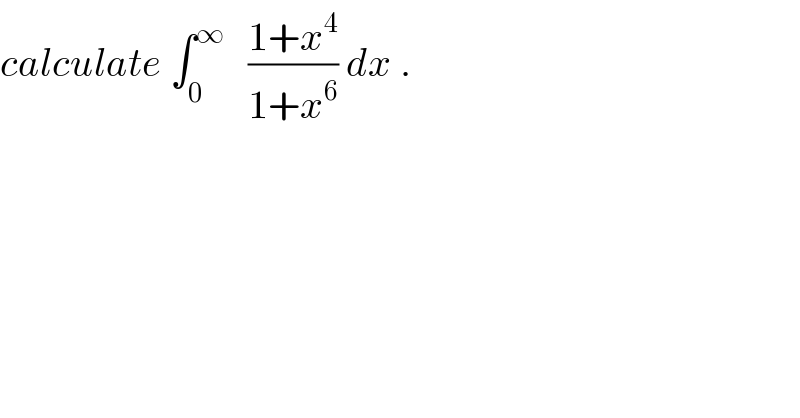 | ||
Commented by abdo imad last updated on 09/Apr/18 | ||
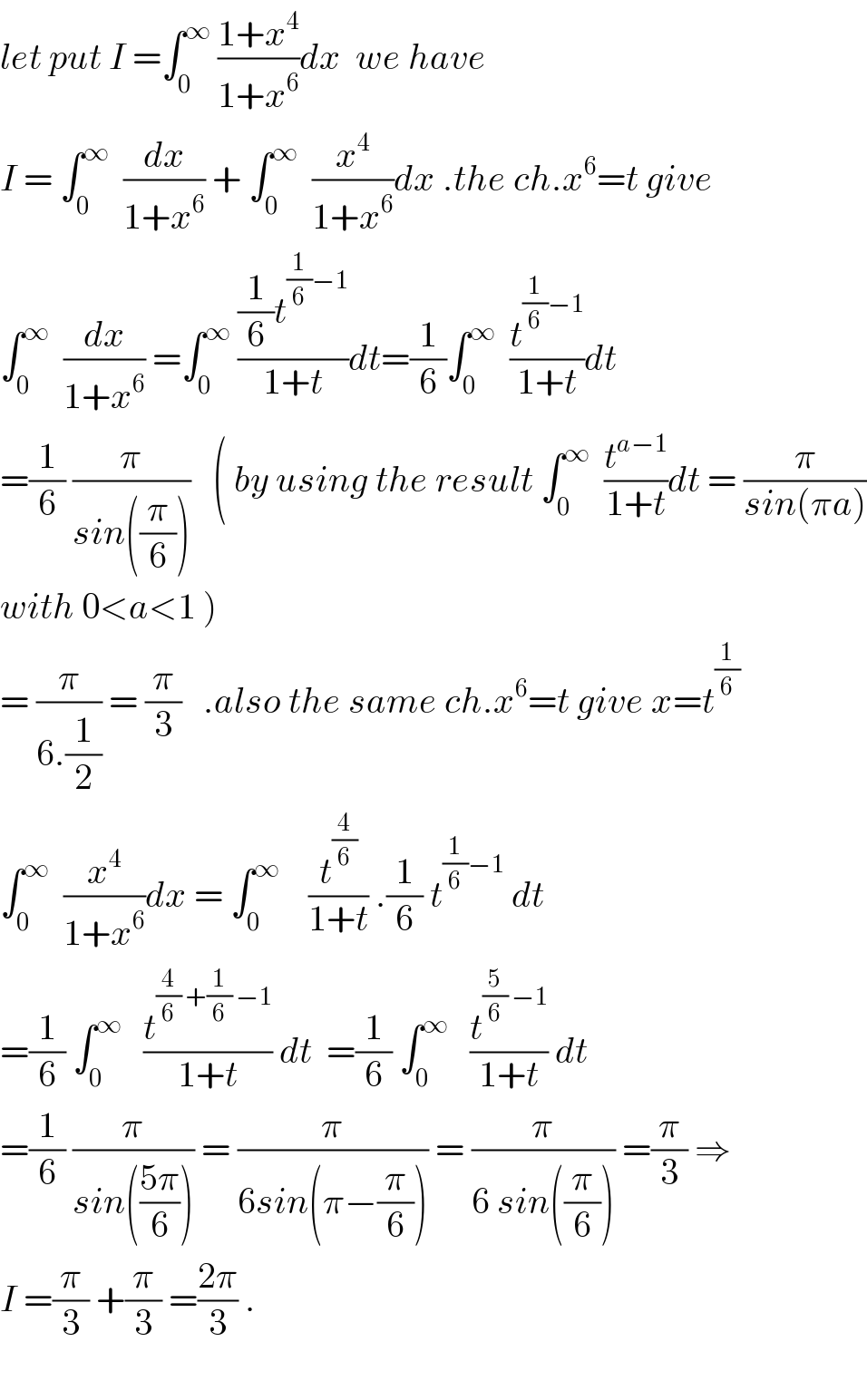 | ||
Answered by Joel578 last updated on 09/Apr/18 | ||
![I = lim_(n→∞) (∫_0 ^n ((x^4 + 1)/(x^6 + 1)) dx) ∫ ((x^4 + 1)/(x^6 + 1)) dx = ∫ ((x^4 + 1 + x^2 − x^2 )/((x^2 +1)(x^4 − x^2 + 1))) dx = ∫ (1/(x^2 + 1)) dx + ∫ (x^2 /(x^6 + 1)) dx = tan^(−1) x + ∫ (x^2 /(x^6 + 1)) dx (u = x^3 → du = 3x^2 dx) = tan^(−1) x + (1/3) ∫ (1/(u^2 + 1)) du = tan^(−1) x + (1/3)tan^(−1) u + C = tan^(−1) (x) + (1/3)tan^(−1) (x^3 ) + C I = lim_(n→∞) [tan^(−1) (x) + (1/3)tan^(−1) (x^3 )]_0 ^n = lim_(n→∞) (tan^(−1) (n) + (1/3)tan^(−1) (n^3 )) − (tan^(−1) (0) + (1/3)tan^(−1) (0)) = (π/2) + (1/3)((π/2)) − 0 = ((2π)/3)](Q33030.png) | ||
| ||