Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 33032 by rahul 19 last updated on 09/Apr/18

f:N→R f(1)=2005. and f(1)+f(2)+......+f(n)= n^2 f(n),n>1. Then f(2004)=?

$${f}:{N}\rightarrow{R} \\ $$ $${f}\left(\mathrm{1}\right)=\mathrm{2005}. \\ $$ $${and}\: \\ $$ $${f}\left(\mathrm{1}\right)+{f}\left(\mathrm{2}\right)+......+{f}\left({n}\right)=\:{n}^{\mathrm{2}} \:{f}\left({n}\right),{n}>\mathrm{1}. \\ $$ $${Then}\:{f}\left(\mathrm{2004}\right)=? \\ $$

Commented byJoel578 last updated on 09/Apr/18

The denomitator form a series 1 3_(⌣) 6_(⌣) 10_(⌣) 15_(⌣) 21_(⌣) , ... +2 +3 +4 +5 +6 Suppose the general term T_n = an^2 + bn + c T_1 = a + b + c = 1 T_2 = 4a + 2b + c = 3 T_3 = 9a + 3b + c = 6 After few calculations, you will found a = (1/2), b = (1/2), c = 0 → T_n = (n^2 /2) + (n/2) = (n/2)(n + 1)

$$\mathrm{The}\:\mathrm{denomitator}\:\mathrm{form}\:\mathrm{a}\:\mathrm{series} \\ $$ $$\underset{\smile} {\mathrm{1}\:\:\:\:\:\mathrm{3}}\underset{\smile} {\:\:\:\:\:\:\mathrm{6}}\underset{\smile} {\:\:\:\:\:\:\mathrm{10}}\underset{\smile} {\:\:\:\:\:\:\mathrm{15}}\underset{\smile} {\:\:\:\:\:\:\mathrm{21}},\:... \\ $$ $$\:+\mathrm{2}\:\:+\mathrm{3}\:\:+\mathrm{4}\:\:\:\:\:+\mathrm{5}\:\:\:\:\:+\mathrm{6} \\ $$ $$ \\ $$ $$\mathrm{Suppose}\:\mathrm{the}\:\mathrm{general}\:\mathrm{term}\:{T}_{{n}} \:=\:{an}^{\mathrm{2}} \:+\:{bn}\:+\:{c} \\ $$ $${T}_{\mathrm{1}} \:=\:{a}\:+\:{b}\:+\:{c}\:=\:\mathrm{1} \\ $$ $${T}_{\mathrm{2}} \:=\:\mathrm{4}{a}\:+\:\mathrm{2}{b}\:+\:{c}\:=\:\mathrm{3} \\ $$ $${T}_{\mathrm{3}} \:=\:\mathrm{9}{a}\:+\:\mathrm{3}{b}\:+\:{c}\:=\:\mathrm{6} \\ $$ $$\mathrm{After}\:\mathrm{few}\:\mathrm{calculations},\:\mathrm{you}\:\mathrm{will}\:\mathrm{found} \\ $$ $${a}\:=\:\frac{\mathrm{1}}{\mathrm{2}},\:{b}\:=\:\frac{\mathrm{1}}{\mathrm{2}},\:{c}\:=\:\mathrm{0} \\ $$ $$\rightarrow\:{T}_{{n}} \:=\:\frac{{n}^{\mathrm{2}} }{\mathrm{2}}\:+\:\frac{{n}}{\mathrm{2}}\:=\:\frac{{n}}{\mathrm{2}}\left({n}\:+\:\mathrm{1}\right) \\ $$

Commented byJoel578 last updated on 09/Apr/18

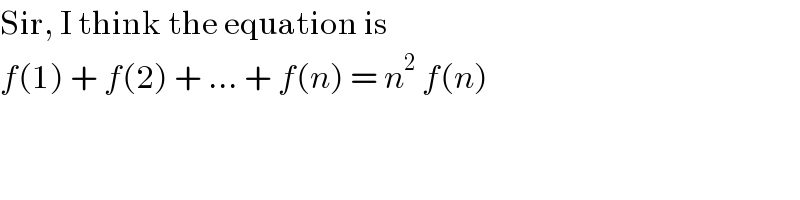
Sir, I think the equation is f(1) + f(2) + ... + f(n) = n^2 f(n)

$$\mathrm{Sir},\:\mathrm{I}\:\mathrm{think}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{is} \\ $$ $${f}\left(\mathrm{1}\right)\:+\:{f}\left(\mathrm{2}\right)\:+\:...\:+\:{f}\left({n}\right)\:=\:{n}^{\mathrm{2}} \:{f}\left({n}\right) \\ $$

Commented byrahul 19 last updated on 09/Apr/18

Joel sir, suppose we are not able to see the pattern at the first sight. Then how can we find the general term ?

$${Joel}\:{sir},\:{suppose}\:{we}\:{are}\:{not}\:{able}\:{to} \\ $$ $${see}\:{the}\:{pattern}\:{at}\:{the}\:{first}\:{sight}. \\ $$ $${Then}\:{how}\:{can}\:{we}\:{find}\:{the}\:{general} \\ $$ $${term}\:? \\ $$

Commented byRasheed.Sindhi last updated on 09/Apr/18

Sorry sir I misunderstood then.

$$\mathrm{Sorry}\:\mathrm{sir}\:\mathrm{I}\:\mathrm{misunderstood}\:\mathrm{then}. \\ $$

Commented byrahul 19 last updated on 09/Apr/18

thank u so much sir!

$${thank}\:{u}\:{so}\:{much}\:{sir}! \\ $$

Answered by Joel578 last updated on 09/Apr/18

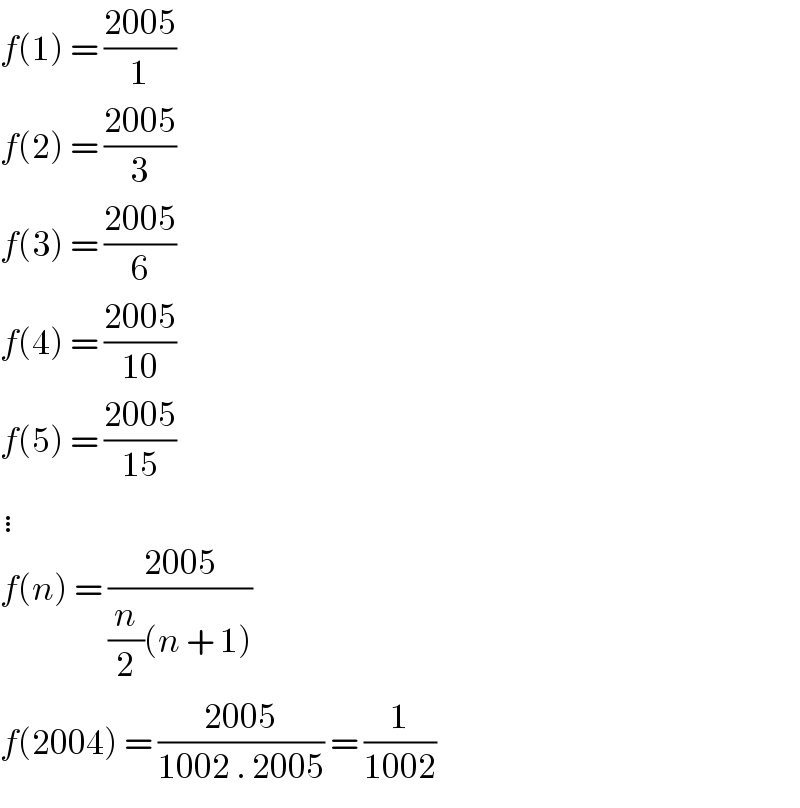
f(1) = ((2005)/1) f(2) = ((2005)/3) f(3) = ((2005)/6) f(4) = ((2005)/(10)) f(5) = ((2005)/(15)) ⋮ f(n) = ((2005)/((n/2)(n + 1))) f(2004) = ((2005)/(1002 . 2005)) = (1/(1002))

$${f}\left(\mathrm{1}\right)\:=\:\frac{\mathrm{2005}}{\mathrm{1}} \\ $$ $${f}\left(\mathrm{2}\right)\:=\:\frac{\mathrm{2005}}{\mathrm{3}} \\ $$ $${f}\left(\mathrm{3}\right)\:=\:\frac{\mathrm{2005}}{\mathrm{6}} \\ $$ $${f}\left(\mathrm{4}\right)\:=\:\frac{\mathrm{2005}}{\mathrm{10}} \\ $$ $${f}\left(\mathrm{5}\right)\:=\:\frac{\mathrm{2005}}{\mathrm{15}} \\ $$ $$\vdots \\ $$ $${f}\left({n}\right)\:=\:\frac{\mathrm{2005}}{\frac{{n}}{\mathrm{2}}\left({n}\:+\:\mathrm{1}\right)} \\ $$ $${f}\left(\mathrm{2004}\right)\:=\:\frac{\mathrm{2005}}{\mathrm{1002}\:.\:\mathrm{2005}}\:=\:\frac{\mathrm{1}}{\mathrm{1002}} \\ $$

Commented byrahul 19 last updated on 09/Apr/18

thank u sir!

$${thank}\:{u}\:{sir}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com