
Question and Answers Forum
Question Number 33064 by artibunja last updated on 09/Apr/18
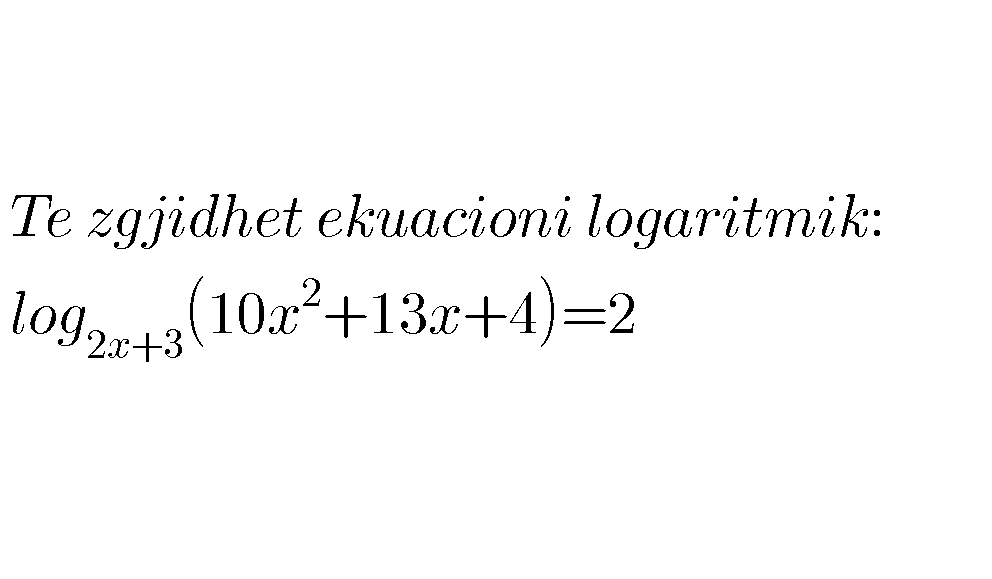
Commented by abdo imad last updated on 09/Apr/18
![we must have 2x+3>0 and 10x^2 +13x +4>0 Δ =13^2 −4 ×10 ×4 =169 −160 =9 >0 x_1 =((−13 +3)/(20))=−(1/2) , x_2 = ((−13 −3)/(20)) =((−16)/(20)) =−(4/5) we must have x∈(]−∞,−(4/5)[∪]−(1/2),+∞[)∩]−(3/2),+∞[ ⇒ x∈]−(3/2),−(4/5)[∪]−(1/2),+∞[ (e)⇔ ((ln(10x^2 +13x +4))/(ln(2x+3))) =2 ⇔ ln(10x^2 +13x +4)=ln((2x+3)^2 )⇔ 10x^2 +13x +4 =4x^2 +12x +9 ⇔ 6x^2 +x −5 =0 Δ =1 −4.6.(−5) =121 ⇒ x_(1 ) =((−1 +11)/(12)) =((10)/(12)) =(5/6) x_2 =((−1−11)/(12)) =−1 but −1 ∈ D_((e)) , (5/6) ∈ D_((e)) ⇒ −1 and (5/6) are the solutions of this equation.](Q33070.png)
Commented by abdo imad last updated on 09/Apr/18
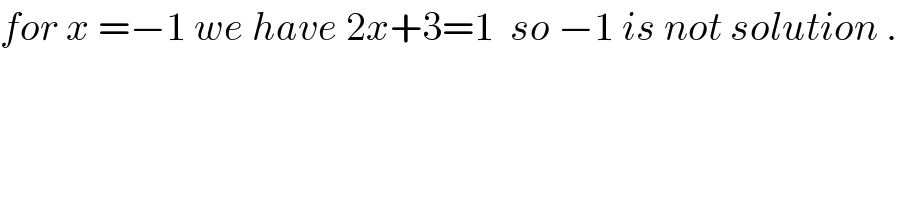
Answered by Rasheed.Sindhi last updated on 10/Apr/18
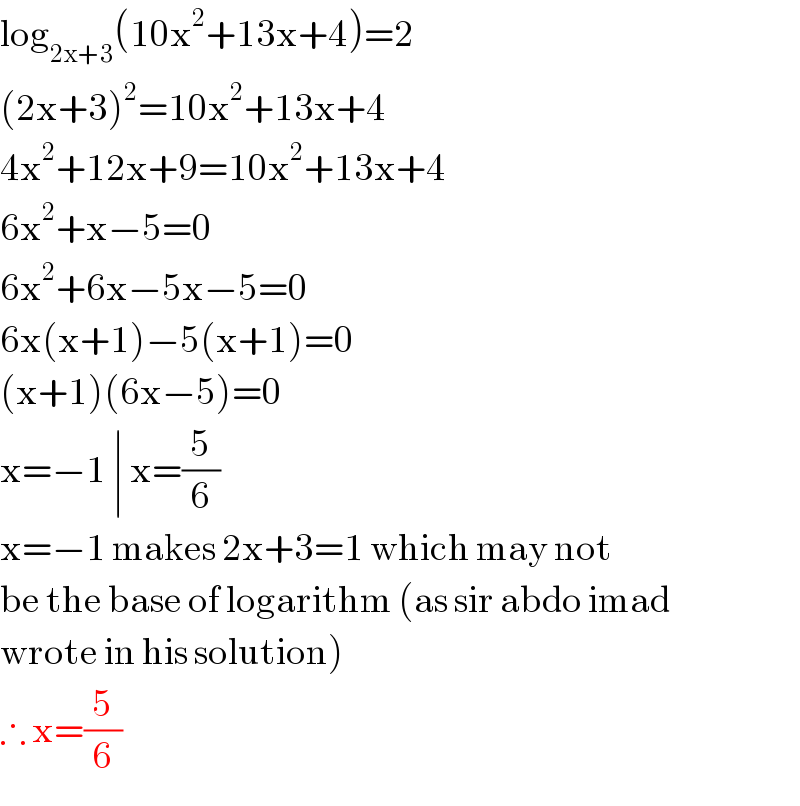
| ||
Question and Answers Forum | ||
Question Number 33064 by artibunja last updated on 09/Apr/18 | ||
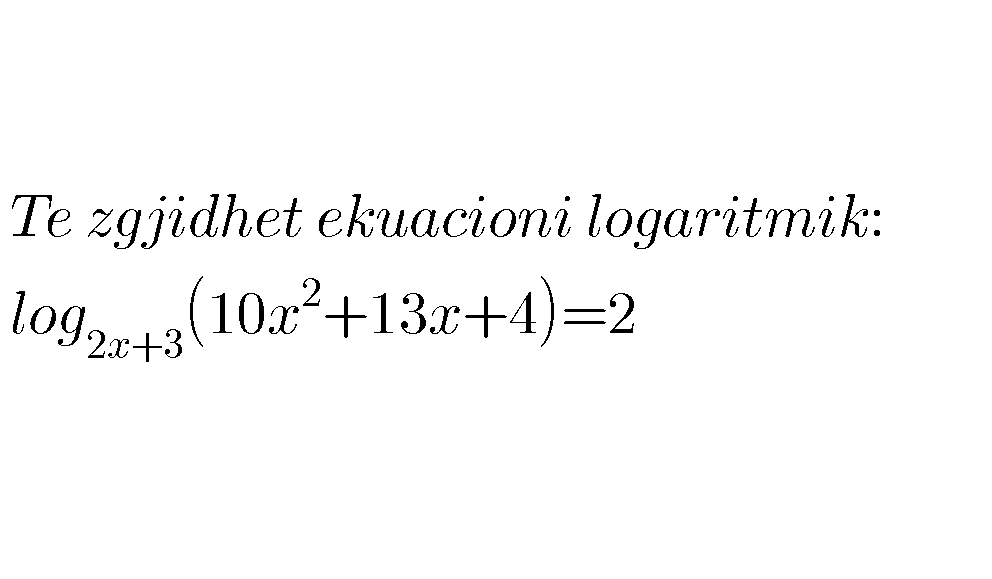 | ||
Commented by abdo imad last updated on 09/Apr/18 | ||
![we must have 2x+3>0 and 10x^2 +13x +4>0 Δ =13^2 −4 ×10 ×4 =169 −160 =9 >0 x_1 =((−13 +3)/(20))=−(1/2) , x_2 = ((−13 −3)/(20)) =((−16)/(20)) =−(4/5) we must have x∈(]−∞,−(4/5)[∪]−(1/2),+∞[)∩]−(3/2),+∞[ ⇒ x∈]−(3/2),−(4/5)[∪]−(1/2),+∞[ (e)⇔ ((ln(10x^2 +13x +4))/(ln(2x+3))) =2 ⇔ ln(10x^2 +13x +4)=ln((2x+3)^2 )⇔ 10x^2 +13x +4 =4x^2 +12x +9 ⇔ 6x^2 +x −5 =0 Δ =1 −4.6.(−5) =121 ⇒ x_(1 ) =((−1 +11)/(12)) =((10)/(12)) =(5/6) x_2 =((−1−11)/(12)) =−1 but −1 ∈ D_((e)) , (5/6) ∈ D_((e)) ⇒ −1 and (5/6) are the solutions of this equation.](Q33070.png) | ||
Commented by abdo imad last updated on 09/Apr/18 | ||
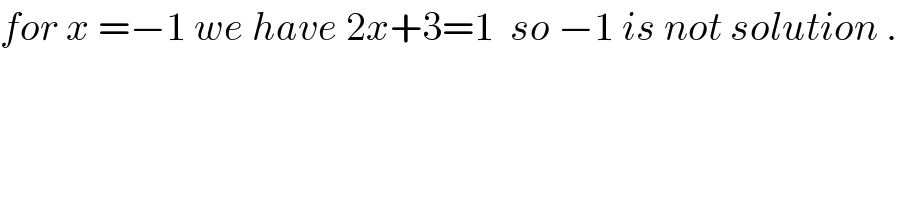 | ||
Answered by Rasheed.Sindhi last updated on 10/Apr/18 | ||
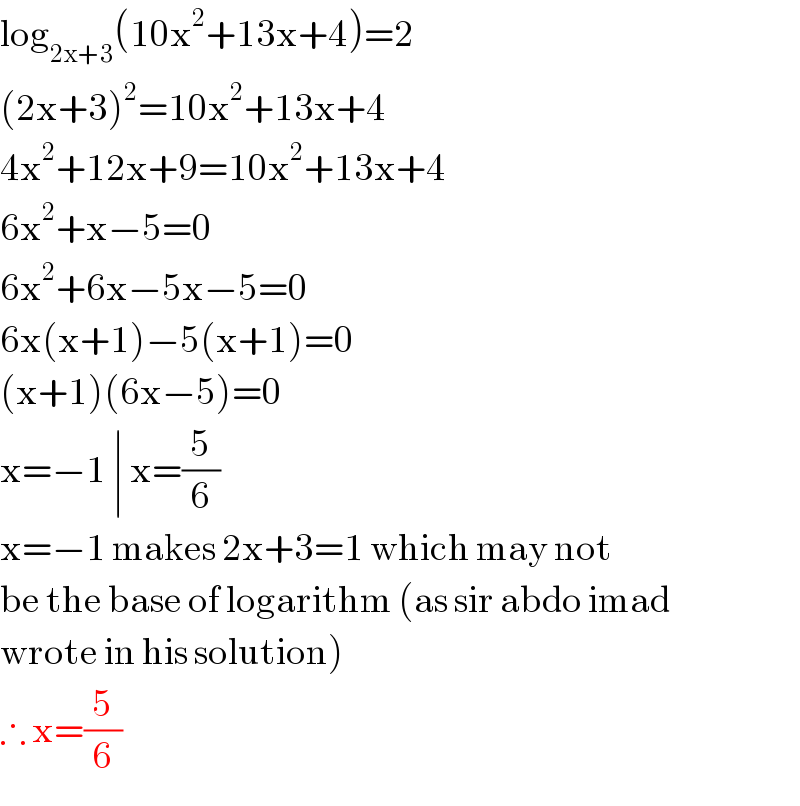 | ||
| ||