
Question and Answers Forum
Question Number 33145 by Ahmad Hajjaj last updated on 11/Apr/18
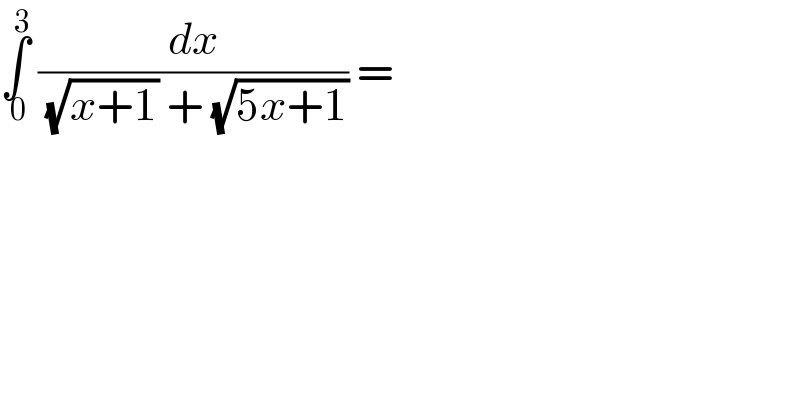
Commented by prof Abdo imad last updated on 11/Apr/18
![I = ∫_0 ^3 (dx/((√(x+1)) +(√(5x+1)))) .ch. (√(x+1)) =t ⇒ I = ∫_1 ^2 ((2tdt)/(t +(√(5(t^2 −1)+1)))) = ∫_1 ^2 ((2tdt)/(t +(√( 5t^2 −4)))) = ∫_1 ^2 ((2dt)/(1 +(√((5t^2 −4)/t^2 )))) = ∫_1 ^2 ((2dt)/(1+(√(5 −(4/t^2 ))))) after we use the ch. (2/t) =(√5) sinx ⇒ (t/2) = (1/((√5) sinx)) ⇒t = (2/((√5) sinx)) dt =−(2/(√5)) ((cosx)/(sin^2 x)) and x =arcsin((2/(t(√5)))) I = ∫_(arcsin((2/(√5)))) ^(arcsin((1/(√5)))) (1/(1+(√5) (√(1−sin^2 x)))) −(2/(√5)) ((cosx)/(sin^2 x))dx = −(2/(√5))∫_(arcsin((2/(√5)))) ^(arcsin((1/(√5)))) ((cosx)/(sin^2 x(1+(√5) cosx)))dx ∫_α ^β −((cosx)/(sin^2 x(1+(√5) cosx))) (by parts) = [ (1/(sinx)) (1/(1+(√5) cosx))]_α ^β − ∫_α ^β (1/(sinx)) (((√5) sinx)/((1+(√5) cosx)^2 ))dx =(1/(sinβ(1+(√5) cosβ))) − (1/(sinα(1+(√5) cosα))) −(√5) ∫_α ^β (dx/((1+(√5) cosx)^2 )) and this integral is calculable by ch. tan((x/2)) =u .... α=arcsin((2/(√5))) and β = arcsin((1/(√5))).](Q33149.png)
Answered by MJS last updated on 11/Apr/18
![(1/(a+b))=((a−b)/((a+b)(a−b)))=((a−b)/(a^2 −b^2 )) (1/((√(x+1))+(√(5x+1))))=(((√(x+1))−(√(5x+1)))/(x+1−5x−1))= =(((√(5x+1))−(√(x+1)))/(4x)) ∫_0 ^3 (dx/((√(x+1))+(√(5x+1))))=(1/4)[(∫((√(5x+1))/x)dx−∫((√(x+1))/x)dx)]_0 ^3 = (∫((√(ax+b))/x)dx with b>0)= =2(√(ax+b))+(√b)×ln∣(((√(ax+b))−(√b))/((√(ax+b))+(√b)))∣ =(1/4)[((2(√(5x+1))+ln∣(((√(5x+1))−1)/((√(5x+1))+1))∣)−(2(√(x+1))+ln∣(((√(x+1))−1)/((√(x+1))+1))∣))]_0 ^3 = =(1/4)[2((√(5x+1))−(√(x+1)))+ln((√(5x+1))−1)−ln((√(5x+1))+1)−ln((√(x+1))−1)+ln((√(x+1))+1)]_0 ^3 = =(1/4)[2((√(5x+1))−(√(x+1)))+ln(((√(x+1))+1)/((√(5x+1))+1))+ln(((√(5x+1))−1)/((√(x+1))−1))]_0 ^3 = lim_(x→0) (((√(5x+1))−1)/((√(x+1))−1))=5 =1+(1/2)ln (3/5)](Q33150.png)
| ||
Question and Answers Forum | ||
Question Number 33145 by Ahmad Hajjaj last updated on 11/Apr/18 | ||
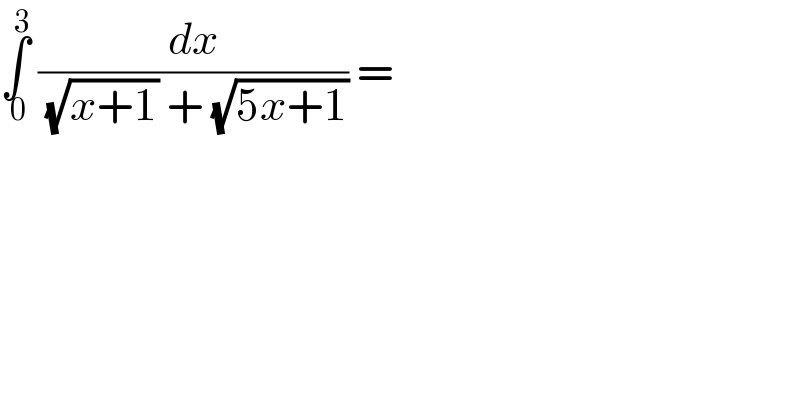 | ||
Commented by prof Abdo imad last updated on 11/Apr/18 | ||
![I = ∫_0 ^3 (dx/((√(x+1)) +(√(5x+1)))) .ch. (√(x+1)) =t ⇒ I = ∫_1 ^2 ((2tdt)/(t +(√(5(t^2 −1)+1)))) = ∫_1 ^2 ((2tdt)/(t +(√( 5t^2 −4)))) = ∫_1 ^2 ((2dt)/(1 +(√((5t^2 −4)/t^2 )))) = ∫_1 ^2 ((2dt)/(1+(√(5 −(4/t^2 ))))) after we use the ch. (2/t) =(√5) sinx ⇒ (t/2) = (1/((√5) sinx)) ⇒t = (2/((√5) sinx)) dt =−(2/(√5)) ((cosx)/(sin^2 x)) and x =arcsin((2/(t(√5)))) I = ∫_(arcsin((2/(√5)))) ^(arcsin((1/(√5)))) (1/(1+(√5) (√(1−sin^2 x)))) −(2/(√5)) ((cosx)/(sin^2 x))dx = −(2/(√5))∫_(arcsin((2/(√5)))) ^(arcsin((1/(√5)))) ((cosx)/(sin^2 x(1+(√5) cosx)))dx ∫_α ^β −((cosx)/(sin^2 x(1+(√5) cosx))) (by parts) = [ (1/(sinx)) (1/(1+(√5) cosx))]_α ^β − ∫_α ^β (1/(sinx)) (((√5) sinx)/((1+(√5) cosx)^2 ))dx =(1/(sinβ(1+(√5) cosβ))) − (1/(sinα(1+(√5) cosα))) −(√5) ∫_α ^β (dx/((1+(√5) cosx)^2 )) and this integral is calculable by ch. tan((x/2)) =u .... α=arcsin((2/(√5))) and β = arcsin((1/(√5))).](Q33149.png) | ||
Answered by MJS last updated on 11/Apr/18 | ||
![(1/(a+b))=((a−b)/((a+b)(a−b)))=((a−b)/(a^2 −b^2 )) (1/((√(x+1))+(√(5x+1))))=(((√(x+1))−(√(5x+1)))/(x+1−5x−1))= =(((√(5x+1))−(√(x+1)))/(4x)) ∫_0 ^3 (dx/((√(x+1))+(√(5x+1))))=(1/4)[(∫((√(5x+1))/x)dx−∫((√(x+1))/x)dx)]_0 ^3 = (∫((√(ax+b))/x)dx with b>0)= =2(√(ax+b))+(√b)×ln∣(((√(ax+b))−(√b))/((√(ax+b))+(√b)))∣ =(1/4)[((2(√(5x+1))+ln∣(((√(5x+1))−1)/((√(5x+1))+1))∣)−(2(√(x+1))+ln∣(((√(x+1))−1)/((√(x+1))+1))∣))]_0 ^3 = =(1/4)[2((√(5x+1))−(√(x+1)))+ln((√(5x+1))−1)−ln((√(5x+1))+1)−ln((√(x+1))−1)+ln((√(x+1))+1)]_0 ^3 = =(1/4)[2((√(5x+1))−(√(x+1)))+ln(((√(x+1))+1)/((√(5x+1))+1))+ln(((√(5x+1))−1)/((√(x+1))−1))]_0 ^3 = lim_(x→0) (((√(5x+1))−1)/((√(x+1))−1))=5 =1+(1/2)ln (3/5)](Q33150.png) | ||
| ||