
Question and Answers Forum
Question Number 33169 by abdo imad last updated on 11/Apr/18
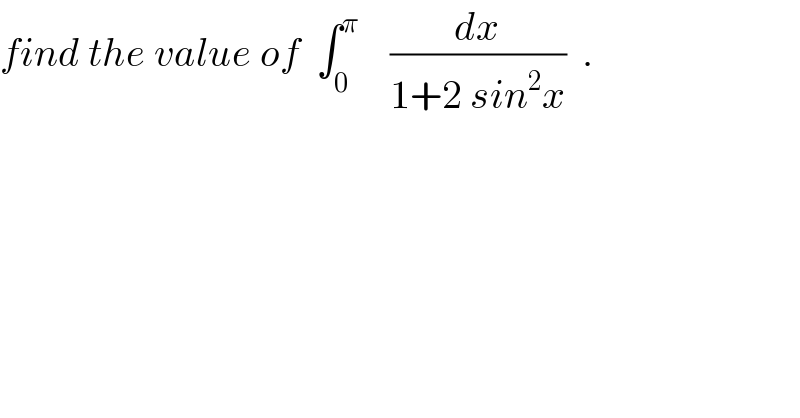
Commented by abdo imad last updated on 12/Apr/18
![let put I =∫_0 ^π (dx/(1+2sin^2 x)) =∫_0 ^π (dx/(1+2(1−cos^2 x))) = ∫_0 ^π (dx/(3 −2cos^2 x)) =∫_0 ^(π/2) (dx/(3 −2 cos^2 x)) + ∫_(π/2) ^π (dx/(3 −2cos^2 x)) =I_1 +I_2 but we knew that 1+tan^2 t =(1/(cos^2 t)) ⇒ cos^2 x = (1/(1+tan^2 x)) ⇒ I_1 = ∫_0 ^(π/2) (dx/(3 −(2/(1+tan^2 x)))) = ∫_0 ^(π/2) ((1+tan^2 x)/(1+3tan^2 x))dx = _(tanx =t) ∫_0 ^(+∞) ((1+t^2 )/(1+3t^2 )) (dt/(1+t^2 )) =∫_0 ^∞ (dt/(1+3t^2 )) =_(t(√3) =u) ∫_0 ^∞ (1/(1+u^2 )) (du/(√3)) =(1/(√3)) [arctanu]_0 ^(+∞) I_1 =(π/(2(√3))) let find I_2 ? I_2 = ∫_(π/2) ^π (dx/(3 −2 cos^2 x)) =_(x = π −t) ∫_(π/2) ^0 ((−dt)/(3 −2 cos^2 t)) =∫_0 ^(π/2) (dt/(3−2cos^2 t)) =I_1 =(π/(2(√3))) ⇒ I = (π/(2(√3))) +(π/(2(√3))) = (π/(√3)) . ★ I =(π/(√3)) ★](Q33180.png)
Answered by sma3l2996 last updated on 11/Apr/18
![I=∫_0 ^π (dx/(1+2sin^2 x)) t=tanx⇒dx=(dt/(1+t^2 )) sin^2 x=(t^2 /(1+t^2 )) I=∫_0 ^∞ (dt/(1+t^2 +2t^2 ))=∫_0 ^∞ (dt/(3t^2 +1)) u=(√3)x⇒dx=((√3)/3)du I=((√3)/3)∫_0 ^∞ (du/(u^2 +1))=((√3)/3)[tan^(−1) (u)]_0 ^∞ I=((√3)/6)π](Q33177.png)
Commented by abdo imad last updated on 12/Apr/18
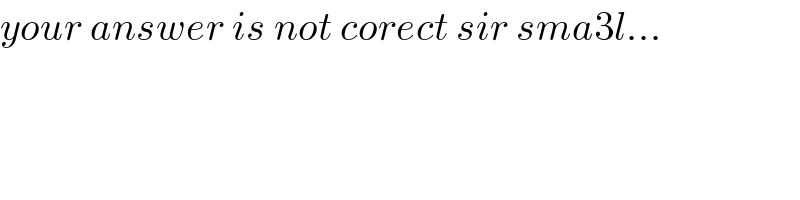
| ||
Question and Answers Forum | ||
Question Number 33169 by abdo imad last updated on 11/Apr/18 | ||
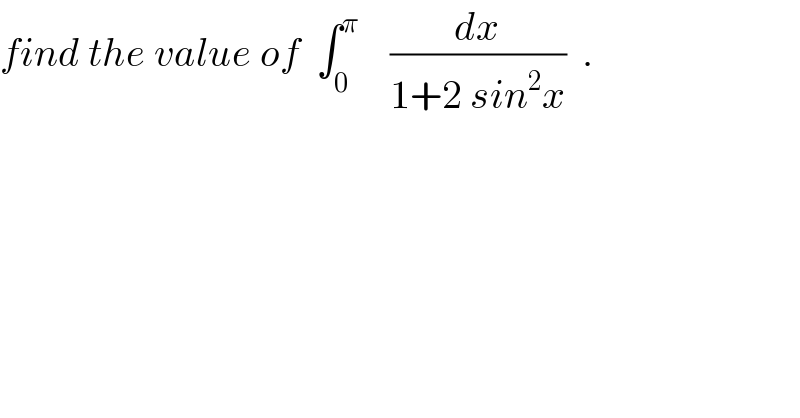 | ||
Commented by abdo imad last updated on 12/Apr/18 | ||
![let put I =∫_0 ^π (dx/(1+2sin^2 x)) =∫_0 ^π (dx/(1+2(1−cos^2 x))) = ∫_0 ^π (dx/(3 −2cos^2 x)) =∫_0 ^(π/2) (dx/(3 −2 cos^2 x)) + ∫_(π/2) ^π (dx/(3 −2cos^2 x)) =I_1 +I_2 but we knew that 1+tan^2 t =(1/(cos^2 t)) ⇒ cos^2 x = (1/(1+tan^2 x)) ⇒ I_1 = ∫_0 ^(π/2) (dx/(3 −(2/(1+tan^2 x)))) = ∫_0 ^(π/2) ((1+tan^2 x)/(1+3tan^2 x))dx = _(tanx =t) ∫_0 ^(+∞) ((1+t^2 )/(1+3t^2 )) (dt/(1+t^2 )) =∫_0 ^∞ (dt/(1+3t^2 )) =_(t(√3) =u) ∫_0 ^∞ (1/(1+u^2 )) (du/(√3)) =(1/(√3)) [arctanu]_0 ^(+∞) I_1 =(π/(2(√3))) let find I_2 ? I_2 = ∫_(π/2) ^π (dx/(3 −2 cos^2 x)) =_(x = π −t) ∫_(π/2) ^0 ((−dt)/(3 −2 cos^2 t)) =∫_0 ^(π/2) (dt/(3−2cos^2 t)) =I_1 =(π/(2(√3))) ⇒ I = (π/(2(√3))) +(π/(2(√3))) = (π/(√3)) . ★ I =(π/(√3)) ★](Q33180.png) | ||
Answered by sma3l2996 last updated on 11/Apr/18 | ||
![I=∫_0 ^π (dx/(1+2sin^2 x)) t=tanx⇒dx=(dt/(1+t^2 )) sin^2 x=(t^2 /(1+t^2 )) I=∫_0 ^∞ (dt/(1+t^2 +2t^2 ))=∫_0 ^∞ (dt/(3t^2 +1)) u=(√3)x⇒dx=((√3)/3)du I=((√3)/3)∫_0 ^∞ (du/(u^2 +1))=((√3)/3)[tan^(−1) (u)]_0 ^∞ I=((√3)/6)π](Q33177.png) | ||
| ||
Commented by abdo imad last updated on 12/Apr/18 | ||
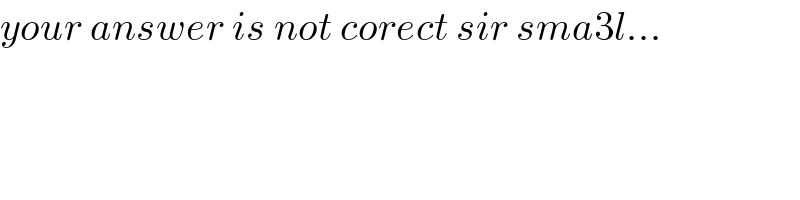 | ||