
Question and Answers Forum
Question Number 33170 by prof Abdo imad last updated on 11/Apr/18
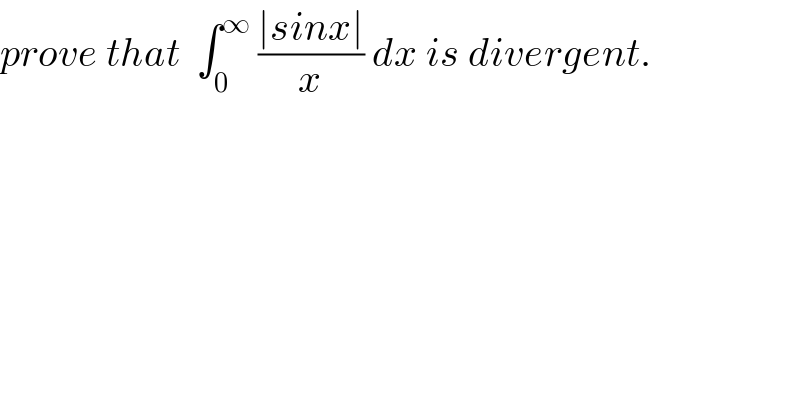
Commented by prof Abdo imad last updated on 13/Apr/18
![∫_0 ^∞ ((∣sinx∣)/x)dx =lim_(n→+∞) A_n with A_n = ∫_0 ^(nπ) ((∣sinx∣)/x)dx but A_n = Σ_(k=0) ^n ∫_(kπ) ^((k+1)π) ((∣sinx∣)/x)dx =_(x=kπ +t) Σ_(k=0) ^n ∫_0 ^π ((sint)/(kπ +t)) dt but 0≤t≤π ⇒ kπ ≤ kπ +t ≤(k+1)π ⇒ (1/((k+1)π)) ≤ (1/(kπ+t)) ≤ (1/(kπ)) ⇒ ((sint)/(kπ+t)) ≥ ((sint)/((k+1)π)) ∀ t∈[0,π] ⇒ ∫_0 ^π ((sint)/(kπ+t)) dt ≥ (1/((k+1)π)) ∫_0 ^π sintdt = (2/((k+1)π)) ⇒ A_n ≥ (2/π) Σ_(k=0) ^n (1/(k+1)) ⇒ A_n ≥ (2/π) Σ_(k=1) ^(n+1) (1/k) ⇒ A_n ≥ (2/π) H_(n+1) _(n→+∞) →+∞ so lim_(n→+∞) A_n =+∞ and the integral is divergent.](Q33234.png)
| ||
Question and Answers Forum | ||
Question Number 33170 by prof Abdo imad last updated on 11/Apr/18 | ||
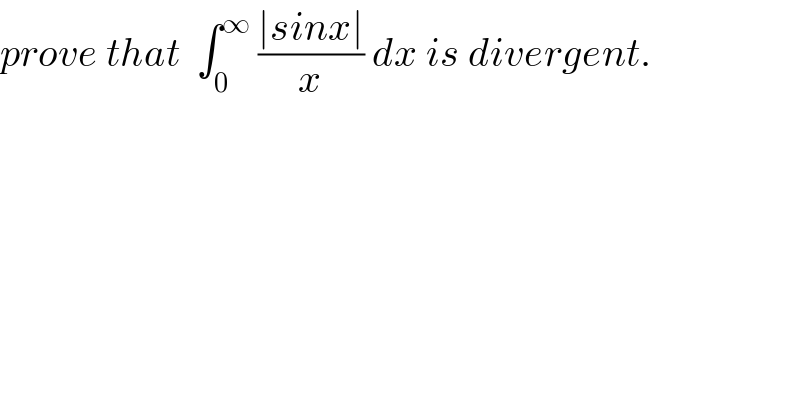 | ||
Commented by prof Abdo imad last updated on 13/Apr/18 | ||
![∫_0 ^∞ ((∣sinx∣)/x)dx =lim_(n→+∞) A_n with A_n = ∫_0 ^(nπ) ((∣sinx∣)/x)dx but A_n = Σ_(k=0) ^n ∫_(kπ) ^((k+1)π) ((∣sinx∣)/x)dx =_(x=kπ +t) Σ_(k=0) ^n ∫_0 ^π ((sint)/(kπ +t)) dt but 0≤t≤π ⇒ kπ ≤ kπ +t ≤(k+1)π ⇒ (1/((k+1)π)) ≤ (1/(kπ+t)) ≤ (1/(kπ)) ⇒ ((sint)/(kπ+t)) ≥ ((sint)/((k+1)π)) ∀ t∈[0,π] ⇒ ∫_0 ^π ((sint)/(kπ+t)) dt ≥ (1/((k+1)π)) ∫_0 ^π sintdt = (2/((k+1)π)) ⇒ A_n ≥ (2/π) Σ_(k=0) ^n (1/(k+1)) ⇒ A_n ≥ (2/π) Σ_(k=1) ^(n+1) (1/k) ⇒ A_n ≥ (2/π) H_(n+1) _(n→+∞) →+∞ so lim_(n→+∞) A_n =+∞ and the integral is divergent.](Q33234.png) | ||