
Question and Answers Forum
Question Number 33259 by prof Abdo imad last updated on 14/Apr/18
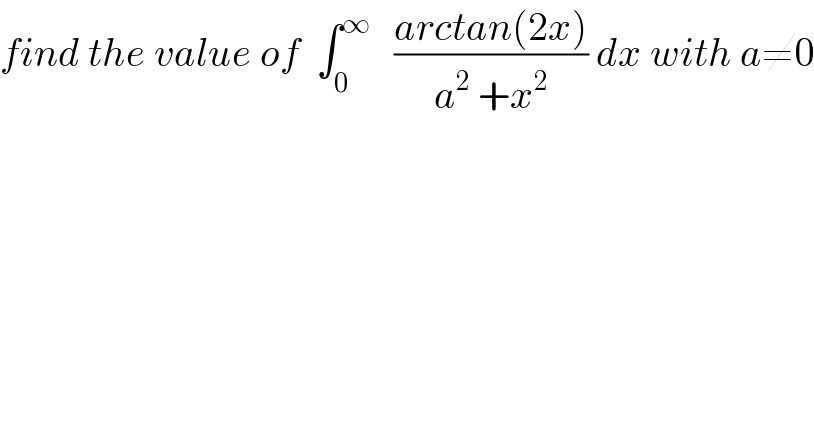
Commented by prof Abdo imad last updated on 27/Apr/18
![let put I= ∫_0 ^∞ ((arctan(2x))/(a^2 +x^2 ))dx if a>0 ch.x=at give I = ∫_0 ^∞ ((arctan(2at))/(a^2 (1+t^2 ))) adt = (1/a)∫_0 ^∞ ((arctan(2at))/(1+t^2 ))dt ⇒aI = ∫_0 ^∞ ((arctan(2at))/(1+t^2 ))dt =f(a) we have f^′ (a) = ∫_0 ^∞ ((2t)/((1+4a^2 t^2 )(1+t^2 )))dt let decompose F(t) = ((2t)/((1+4a^2 t^2 )(1+t^2 ))) = ((αt +b)/(t^2 +1)) + ((ct +d)/(4a^2 t^2 +1)) F(−t)=−F(t) ⇒((−αt+b)/(t^2 +1)) +((−ct +d)/(4a^2 t^2 +1)) =((−αt−b)/(t^2 +1)) +((−ct −d)/(4a^2 t^2 +1)) ⇒ b=d=0 ⇒ F(t)= ((αt)/(t^2 +1)) +((ct)/(4a^2 t^2 +1)) lim_(t→+∞) t F(t) =0 =α +(c/(4a^2 )) ⇒4a^2 α +c =0 ⇒ c=−4a^2 α ⇒F(t)= ((αt)/(t^2 +1)) −4a^2 ((αt)/(4a^2 t^2 +1)) F(1) = (2/((1+4a^2 )2)) =(1/(4a^2 +1)) = (α/2) −((4a^2 α)/(4a^2 +1)) ⇒ 1 =(1/2)(4a^2 +1)α −4a^2 α =(2a^2 +(1/2)−4a^2 )α =((1/2) −2a^2 )α =((1−4a^2 )/2) α ⇒α= (2/(1−4a^2 )) F(t) =(2/(1−4a^2 )) (t/(t^2 +1)) −4a^2 (2/(1−4a^2 )) (t/(4a^2 t^2 +1)) F(t) = (2/(1−4a^2 )) (t/(t^2 +1)) −((8a^2 )/(1−4a^2 )) (t/(4a^2 t^2 +1)) f^′ (a) = (1/(1−4a^2 )) ∫_0 ^∞ ((2tdt)/(t^2 +1)) −((8a^2 )/(1−4a^2 ))∫_0 ^∞ ((tdt)/(4a^2 t^2 +1)) but ∫_0 ^∞ ((tdt)/(4a^2 t^2 +1)) =(1/(8a^2 ))∫_0 ^∞ ((8a^2 t)/(4a^2 t^2 +1)) f^′ (a)= (1/(1−4a^2 ))[ln(((1+t^2 )/(4a^2 t^2 +1)))]_0 ^(+∞) =(1/(1−4a^2 ))ln((1/(4a^2 ))) = ((−ln(4a^2 ))/(1−4a^2 )) ⇒f(a) = ∫_0 ^a ((−ln(4x^2 ))/(1−4x^2 ))dx +λ but λ =f(0)=0 ⇒f(a) =−∫_0 ^(a ) ((2ln(2x))/(1−4x^2 ))dx −f(a)=_(2x=t) 2 ∫_0 ^(2a) ((ln(t))/(1−t^2 )) (dt/2) = ∫_0 ^(2a) ((ln(t))/(1−t^2 ))dt if0 <2a<1 ⇔ 0<a<(1/2) ∫_0 ^(2a) ((ln(t))/(1−t^2 ))dt = ∫_0 ^(2a) (Σ_(n=0) ^∞ t^(2n) )ln(t)dt = Σ_(n=0) ^∞ ∫_0 ^(2a) t^(2n) ln(t)dt =Σ_(n=0) ^∞ A_n A_n =∫_0 ^(2a) t^(2n) ln(t)dt be calculated by recurrence ....be continued....](Q33906.png)
| ||
Question and Answers Forum | ||
Question Number 33259 by prof Abdo imad last updated on 14/Apr/18 | ||
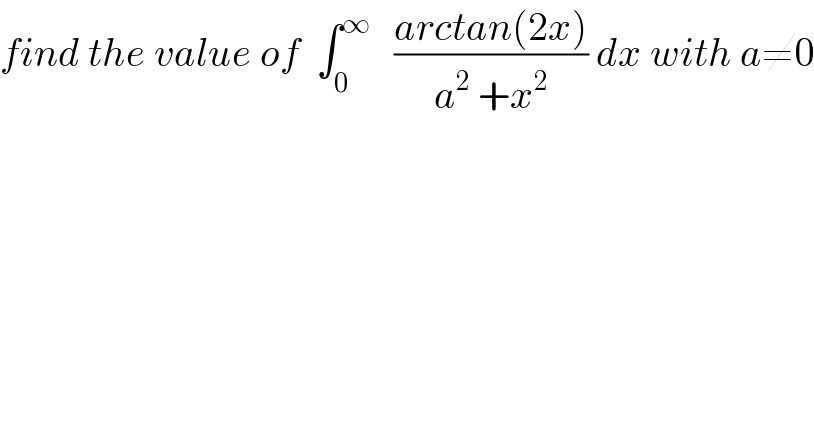 | ||
Commented by prof Abdo imad last updated on 27/Apr/18 | ||
![let put I= ∫_0 ^∞ ((arctan(2x))/(a^2 +x^2 ))dx if a>0 ch.x=at give I = ∫_0 ^∞ ((arctan(2at))/(a^2 (1+t^2 ))) adt = (1/a)∫_0 ^∞ ((arctan(2at))/(1+t^2 ))dt ⇒aI = ∫_0 ^∞ ((arctan(2at))/(1+t^2 ))dt =f(a) we have f^′ (a) = ∫_0 ^∞ ((2t)/((1+4a^2 t^2 )(1+t^2 )))dt let decompose F(t) = ((2t)/((1+4a^2 t^2 )(1+t^2 ))) = ((αt +b)/(t^2 +1)) + ((ct +d)/(4a^2 t^2 +1)) F(−t)=−F(t) ⇒((−αt+b)/(t^2 +1)) +((−ct +d)/(4a^2 t^2 +1)) =((−αt−b)/(t^2 +1)) +((−ct −d)/(4a^2 t^2 +1)) ⇒ b=d=0 ⇒ F(t)= ((αt)/(t^2 +1)) +((ct)/(4a^2 t^2 +1)) lim_(t→+∞) t F(t) =0 =α +(c/(4a^2 )) ⇒4a^2 α +c =0 ⇒ c=−4a^2 α ⇒F(t)= ((αt)/(t^2 +1)) −4a^2 ((αt)/(4a^2 t^2 +1)) F(1) = (2/((1+4a^2 )2)) =(1/(4a^2 +1)) = (α/2) −((4a^2 α)/(4a^2 +1)) ⇒ 1 =(1/2)(4a^2 +1)α −4a^2 α =(2a^2 +(1/2)−4a^2 )α =((1/2) −2a^2 )α =((1−4a^2 )/2) α ⇒α= (2/(1−4a^2 )) F(t) =(2/(1−4a^2 )) (t/(t^2 +1)) −4a^2 (2/(1−4a^2 )) (t/(4a^2 t^2 +1)) F(t) = (2/(1−4a^2 )) (t/(t^2 +1)) −((8a^2 )/(1−4a^2 )) (t/(4a^2 t^2 +1)) f^′ (a) = (1/(1−4a^2 )) ∫_0 ^∞ ((2tdt)/(t^2 +1)) −((8a^2 )/(1−4a^2 ))∫_0 ^∞ ((tdt)/(4a^2 t^2 +1)) but ∫_0 ^∞ ((tdt)/(4a^2 t^2 +1)) =(1/(8a^2 ))∫_0 ^∞ ((8a^2 t)/(4a^2 t^2 +1)) f^′ (a)= (1/(1−4a^2 ))[ln(((1+t^2 )/(4a^2 t^2 +1)))]_0 ^(+∞) =(1/(1−4a^2 ))ln((1/(4a^2 ))) = ((−ln(4a^2 ))/(1−4a^2 )) ⇒f(a) = ∫_0 ^a ((−ln(4x^2 ))/(1−4x^2 ))dx +λ but λ =f(0)=0 ⇒f(a) =−∫_0 ^(a ) ((2ln(2x))/(1−4x^2 ))dx −f(a)=_(2x=t) 2 ∫_0 ^(2a) ((ln(t))/(1−t^2 )) (dt/2) = ∫_0 ^(2a) ((ln(t))/(1−t^2 ))dt if0 <2a<1 ⇔ 0<a<(1/2) ∫_0 ^(2a) ((ln(t))/(1−t^2 ))dt = ∫_0 ^(2a) (Σ_(n=0) ^∞ t^(2n) )ln(t)dt = Σ_(n=0) ^∞ ∫_0 ^(2a) t^(2n) ln(t)dt =Σ_(n=0) ^∞ A_n A_n =∫_0 ^(2a) t^(2n) ln(t)dt be calculated by recurrence ....be continued....](Q33906.png) | ||