
Question and Answers Forum
Question Number 33331 by prof Abdo imad last updated on 14/Apr/18
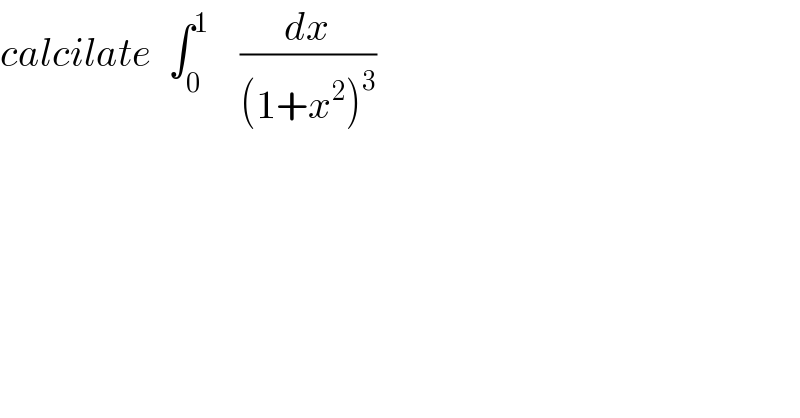
Commented by math khazana by abdo last updated on 19/Apr/18
![let put I = ∫_0 ^1 (dx/((1+x^2 )^3 )) changement x=tantgive I = ∫_0 ^(π/4) (1/((1+tan^2 t)^3 )) (1+tan^2 t)dt = ∫_0 ^( (π/4)) (dt/((1+tan^2 t)^2 )) =∫_0 ^(π/4) cos^4 t dt = ∫_0 ^(π/4) (1/4)(1+cos(2t))^2 dt = (1/4) ∫_0 ^(π/4) (1+2cos(2t) +cos^2 (2t))dt = (π/(16)) +(1/2) ∫_0 ^(π/4) cos(2t) +(1/8) ∫_0 ^(π/4) ( 1+cos(4t))dt = (π/(16)) +(1/4)[sin(2t)]_0 ^(π/4) + (π/(32)) +(1/(32))[ sin(4t)]_0 ^(π/4) = ((3π)/(32)) +(1/4) +0 ⇒ I = (1/4) +((3π)/(32)) .](Q33565.png)
| ||
Question and Answers Forum | ||
Question Number 33331 by prof Abdo imad last updated on 14/Apr/18 | ||
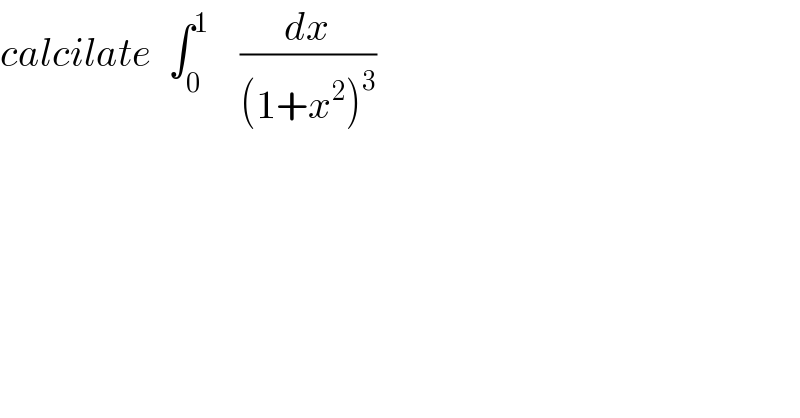 | ||
Commented by math khazana by abdo last updated on 19/Apr/18 | ||
![let put I = ∫_0 ^1 (dx/((1+x^2 )^3 )) changement x=tantgive I = ∫_0 ^(π/4) (1/((1+tan^2 t)^3 )) (1+tan^2 t)dt = ∫_0 ^( (π/4)) (dt/((1+tan^2 t)^2 )) =∫_0 ^(π/4) cos^4 t dt = ∫_0 ^(π/4) (1/4)(1+cos(2t))^2 dt = (1/4) ∫_0 ^(π/4) (1+2cos(2t) +cos^2 (2t))dt = (π/(16)) +(1/2) ∫_0 ^(π/4) cos(2t) +(1/8) ∫_0 ^(π/4) ( 1+cos(4t))dt = (π/(16)) +(1/4)[sin(2t)]_0 ^(π/4) + (π/(32)) +(1/(32))[ sin(4t)]_0 ^(π/4) = ((3π)/(32)) +(1/4) +0 ⇒ I = (1/4) +((3π)/(32)) .](Q33565.png) | ||