
Question and Answers Forum
Question Number 33350 by caravan msup abdo. last updated on 14/Apr/18
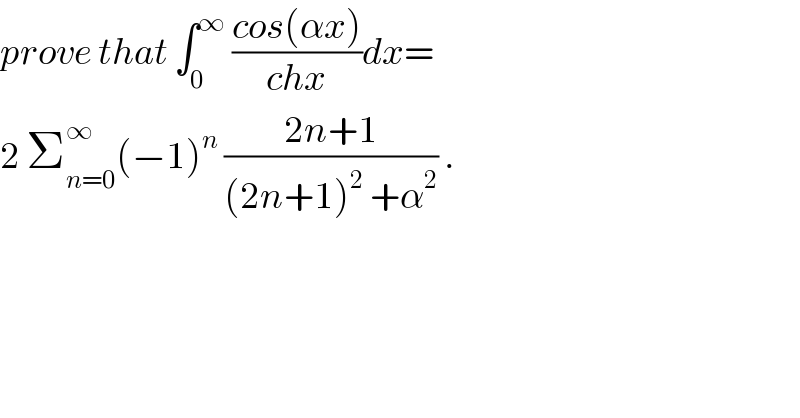
Commented by abdo imad last updated on 17/Apr/18
![let put I =∫_0 ^∞ ((cos(αx))/(chx))dx I = 2 ∫_0 ^∞ ((cos(αx))/(e^x +e^(−x) ))dx =2 ∫_0 ^∞ ((e^(−x) cos(αx))/(1+e^(−2x) ))dx =2 ∫_0 ^∞ (Σ_(n=0) ^∞ (−1)^n e^(−2nx) ) .e^(−x) cos(αx)dx =2 Σ_(n=0) ^∞ (−1)^n ∫_0 ^∞ e^(−(2n+1)x) cos(αx)dx but A_n =∫_0 ^∞ e^(−(2n+1)x) cos(αx)dx = Re( ∫_0 ^∞ e^(−(2n+1)x) e^(−iαx) dx) =Re( ∫_0 ^∞ e^(−(2n+1+iα)x) dx) but we have ∫_0 ^∞ e^(−(2n+1 +iα)x) dx =[−(1/(2n+1 +iα)) e^(−(2n+1 +iα)) ]_0 ^(+∞) =(1/(2n+1+iα)) = ((2n+1−iα)/((2n+1)^2 +α^2 )) ⇒ A_n =((2n+1)/((2n+1)^2 +α^2 )) ⇒ I =2 Σ_(n=0) ^∞ (((−1)^n (2n+1))/((2n+1)^2 +α^2 )) .](Q33490.png)
| ||
Question and Answers Forum | ||
Question Number 33350 by caravan msup abdo. last updated on 14/Apr/18 | ||
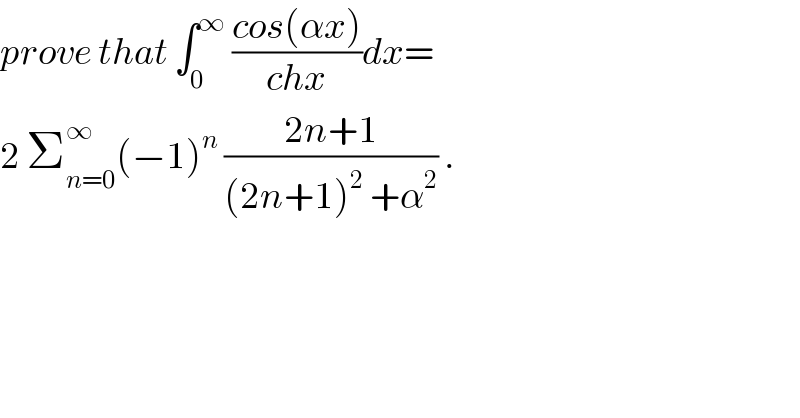 | ||
Commented by abdo imad last updated on 17/Apr/18 | ||
![let put I =∫_0 ^∞ ((cos(αx))/(chx))dx I = 2 ∫_0 ^∞ ((cos(αx))/(e^x +e^(−x) ))dx =2 ∫_0 ^∞ ((e^(−x) cos(αx))/(1+e^(−2x) ))dx =2 ∫_0 ^∞ (Σ_(n=0) ^∞ (−1)^n e^(−2nx) ) .e^(−x) cos(αx)dx =2 Σ_(n=0) ^∞ (−1)^n ∫_0 ^∞ e^(−(2n+1)x) cos(αx)dx but A_n =∫_0 ^∞ e^(−(2n+1)x) cos(αx)dx = Re( ∫_0 ^∞ e^(−(2n+1)x) e^(−iαx) dx) =Re( ∫_0 ^∞ e^(−(2n+1+iα)x) dx) but we have ∫_0 ^∞ e^(−(2n+1 +iα)x) dx =[−(1/(2n+1 +iα)) e^(−(2n+1 +iα)) ]_0 ^(+∞) =(1/(2n+1+iα)) = ((2n+1−iα)/((2n+1)^2 +α^2 )) ⇒ A_n =((2n+1)/((2n+1)^2 +α^2 )) ⇒ I =2 Σ_(n=0) ^∞ (((−1)^n (2n+1))/((2n+1)^2 +α^2 )) .](Q33490.png) | ||