
Question and Answers Forum
Question Number 33351 by caravan msup abdo. last updated on 14/Apr/18
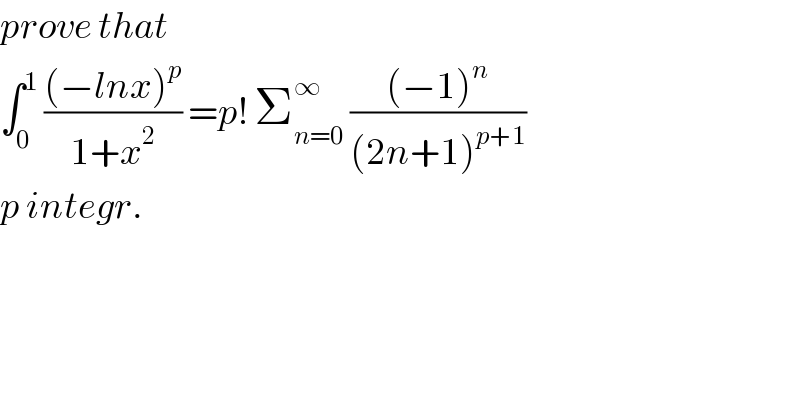
Commented by math khazana by abdo last updated on 19/Apr/18
![let put A_p = ∫_0 ^1 (((−lnx)^p )/(1+x^2 ))dx A_p = (−1)^p ∫_0 ^1 (((lnx)^p )/(1+x^2 ))dx =(−1)^p ∫_0 ^1 ( Σ_(n=0) ^∞ (−1)^n x^(2n) )(lnx)^p dx = Σ_(n=0) ^∞ (−1)^(n+p) ∫_0 ^1 x^(2n) (lnx)^p dx let find I_(n,p) = ∫_0 ^1 x^n (lnx)^p dx by parts I_(n,p) = [(1/(n+1)) x^(n+1) (lnx)^p ]_0 ^1 − ∫_0 ^1 (1/(n+1))x^(n+1) (p/x) (lnx)^(p−1) =−(p/(n+1)) ∫_0 ^1 x^n (lnx)^(p−1) dx =((−p)/(n+1)) I_(n,p−1) ⇒ I_(n,p) = (((−p)(−(p−1)))/((n+1)^2 )) I_(n,p−2) =....= (((−1)^p p!)/((n+1)^p )) I_(n,0) I_(n,0) = ∫_0 ^1 x^n dx = (1/(n+1)) ⇒ I_(n,p) = (((−1)^p p!)/((n+1)^(p+1) )) ⇒ ∫_0 ^1 x^(2n) (lnx)^p dx = (((−1)^p p!)/((2n+1)^(p+1) )) and A_p =Σ_(n=0) ^∞ (−1)^(n+p) (((−1)^p p!)/((2n+1)^(p+1) )) =p! Σ_(n=0) ^∞ (((−1)^n )/((2n+1)^(p+1) )) .](Q33562.png)
| ||
Question and Answers Forum | ||
Question Number 33351 by caravan msup abdo. last updated on 14/Apr/18 | ||
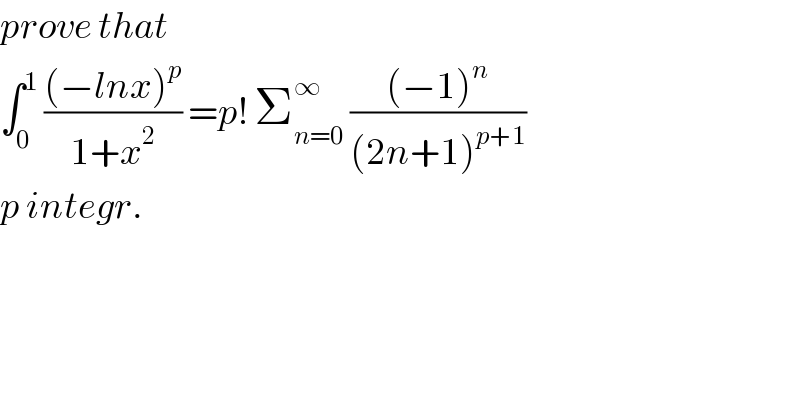 | ||
Commented by math khazana by abdo last updated on 19/Apr/18 | ||
![let put A_p = ∫_0 ^1 (((−lnx)^p )/(1+x^2 ))dx A_p = (−1)^p ∫_0 ^1 (((lnx)^p )/(1+x^2 ))dx =(−1)^p ∫_0 ^1 ( Σ_(n=0) ^∞ (−1)^n x^(2n) )(lnx)^p dx = Σ_(n=0) ^∞ (−1)^(n+p) ∫_0 ^1 x^(2n) (lnx)^p dx let find I_(n,p) = ∫_0 ^1 x^n (lnx)^p dx by parts I_(n,p) = [(1/(n+1)) x^(n+1) (lnx)^p ]_0 ^1 − ∫_0 ^1 (1/(n+1))x^(n+1) (p/x) (lnx)^(p−1) =−(p/(n+1)) ∫_0 ^1 x^n (lnx)^(p−1) dx =((−p)/(n+1)) I_(n,p−1) ⇒ I_(n,p) = (((−p)(−(p−1)))/((n+1)^2 )) I_(n,p−2) =....= (((−1)^p p!)/((n+1)^p )) I_(n,0) I_(n,0) = ∫_0 ^1 x^n dx = (1/(n+1)) ⇒ I_(n,p) = (((−1)^p p!)/((n+1)^(p+1) )) ⇒ ∫_0 ^1 x^(2n) (lnx)^p dx = (((−1)^p p!)/((2n+1)^(p+1) )) and A_p =Σ_(n=0) ^∞ (−1)^(n+p) (((−1)^p p!)/((2n+1)^(p+1) )) =p! Σ_(n=0) ^∞ (((−1)^n )/((2n+1)^(p+1) )) .](Q33562.png) | ||