Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 3370 by Filup last updated on 12/Dec/15

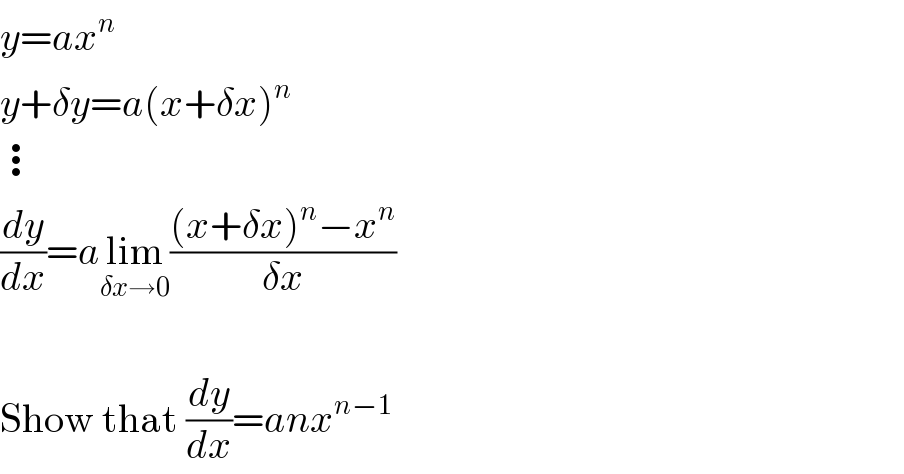
y=ax^n y+δy=a(x+δx)^n ⋮ (dy/dx)=alim_(δx→0) (((x+δx)^n −x^n )/(δx)) Show that (dy/dx)=anx^(n−1)

$${y}={ax}^{{n}} \\ $$$${y}+\delta{y}={a}\left({x}+\delta{x}\right)^{{n}} \\ $$$$\vdots \\ $$$$\frac{{dy}}{{dx}}={a}\underset{\delta{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left({x}+\delta{x}\right)^{{n}} −{x}^{{n}} }{\delta{x}} \\ $$$$ \\ $$$$\mathrm{Show}\:\mathrm{that}\:\frac{{dy}}{{dx}}={anx}^{{n}−\mathrm{1}} \\ $$

Answered by Yozzi last updated on 12/Dec/15

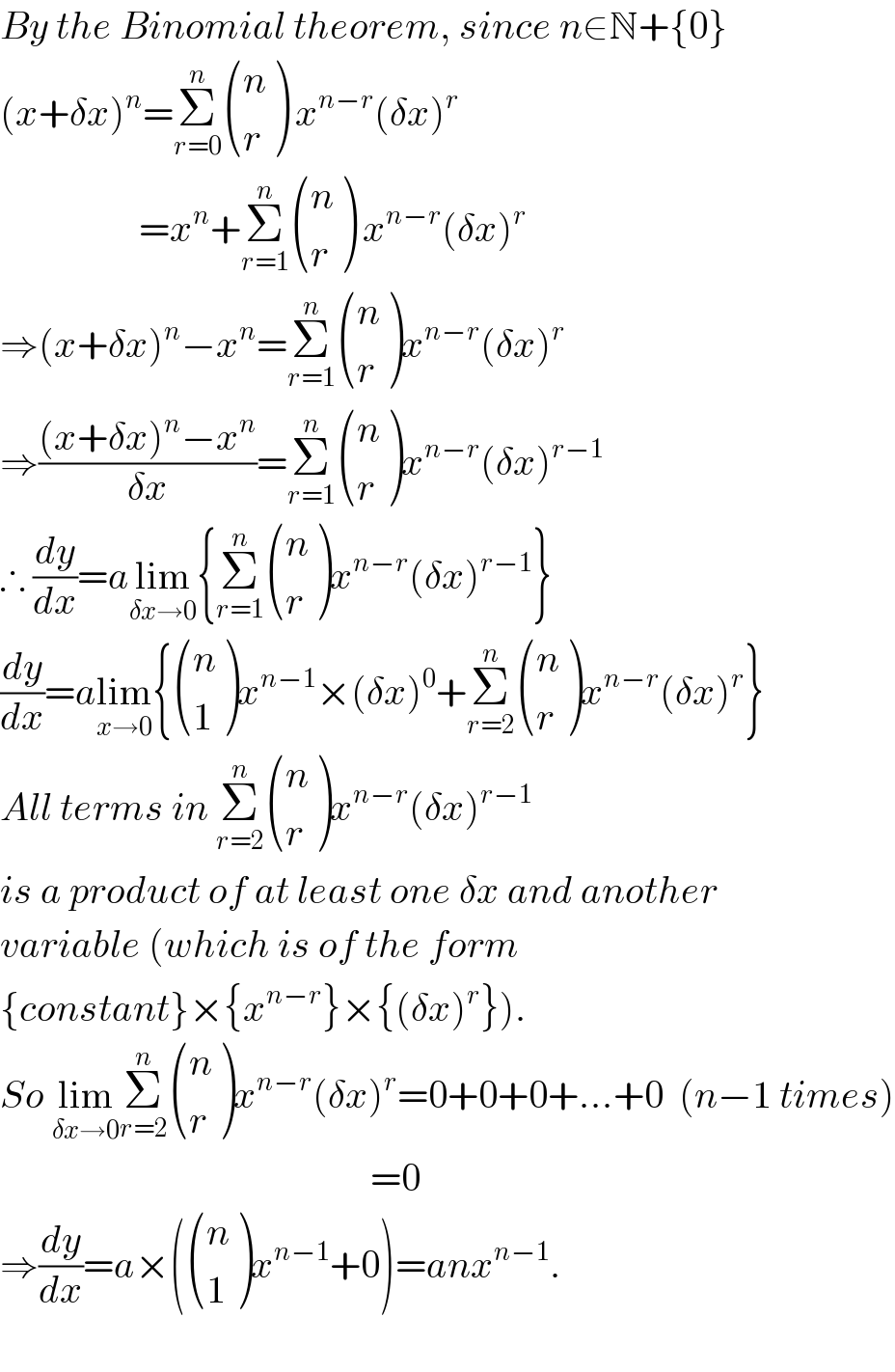
By the Binomial theorem, since n∈N+{0} (x+δx)^n =Σ_(r=0) ^n ((n),(r) ) x^(n−r) (δx)^r =x^n +Σ_(r=1) ^n ((n),(r) ) x^(n−r) (δx)^r ⇒(x+δx)^n −x^n =Σ_(r=1) ^n ((n),(r) )x^(n−r) (δx)^r ⇒(((x+δx)^n −x^n )/(δx))=Σ_(r=1) ^n ((n),(r) )x^(n−r) (δx)^(r−1) ∴ (dy/dx)=alim_(δx→0) {Σ_(r=1) ^n ((n),(r) )x^(n−r) (δx)^(r−1) } (dy/dx)=alim_(x→0) { ((n),(1) )x^(n−1) ×(δx)^0 +Σ_(r=2) ^n ((n),(r) )x^(n−r) (δx)^r } All terms in Σ_(r=2) ^n ((n),(r) )x^(n−r) (δx)^(r−1) is a product of at least one δx and another variable (which is of the form {constant}×{x^(n−r) }×{(δx)^r }). So lim_(δx→0) Σ_(r=2) ^n ((n),(r) )x^(n−r) (δx)^r =0+0+0+...+0 (n−1 times) =0 ⇒(dy/dx)=a×( ((n),(1) )x^(n−1) +0)=anx^(n−1) .

$${By}\:{the}\:{Binomial}\:{theorem},\:{since}\:{n}\in\mathbb{N}+\left\{\mathrm{0}\right\} \\ $$$$\left({x}+\delta{x}\right)^{{n}} =\underset{{r}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{r}}\end{pmatrix}\:{x}^{{n}−{r}} \left(\delta{x}\right)^{{r}} \:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={x}^{{n}} +\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{r}}\end{pmatrix}\:{x}^{{n}−{r}} \left(\delta{x}\right)^{{r}} \\ $$$$\Rightarrow\left({x}+\delta{x}\right)^{{n}} −{x}^{{n}} =\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{r}}\end{pmatrix}{x}^{{n}−{r}} \left(\delta{x}\right)^{{r}} \\ $$$$\Rightarrow\frac{\left({x}+\delta{x}\right)^{{n}} −{x}^{{n}} }{\delta{x}}=\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{r}}\end{pmatrix}{x}^{{n}−{r}} \left(\delta{x}\right)^{{r}−\mathrm{1}} \\ $$$$\therefore\:\frac{{dy}}{{dx}}={a}\underset{\delta{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left\{\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{r}}\end{pmatrix}{x}^{{n}−{r}} \left(\delta{x}\right)^{{r}−\mathrm{1}} \right\} \\ $$$$\frac{{dy}}{{dx}}={a}\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left\{\begin{pmatrix}{{n}}\\{\mathrm{1}}\end{pmatrix}{x}^{{n}−\mathrm{1}} ×\left(\delta{x}\right)^{\mathrm{0}} +\underset{{r}=\mathrm{2}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{r}}\end{pmatrix}{x}^{{n}−{r}} \left(\delta{x}\right)^{{r}} \right\} \\ $$$${All}\:{terms}\:{in}\:\underset{{r}=\mathrm{2}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{r}}\end{pmatrix}{x}^{{n}−{r}} \left(\delta{x}\right)^{{r}−\mathrm{1}} \\ $$$${is}\:{a}\:{product}\:{of}\:{at}\:{least}\:{one}\:\delta{x}\:{and}\:{another} \\ $$$${variable}\:\left({which}\:{is}\:{of}\:{the}\:{form}\:\right. \\ $$$$\left.\left\{{constant}\right\}×\left\{{x}^{{n}−{r}} \right\}×\left\{\left(\delta{x}\right)^{{r}} \right\}\right). \\ $$$${So}\:\underset{\delta{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\underset{{r}=\mathrm{2}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{r}}\end{pmatrix}{x}^{{n}−{r}} \left(\delta{x}\right)^{{r}} =\mathrm{0}+\mathrm{0}+\mathrm{0}+...+\mathrm{0}\:\:\left({n}−\mathrm{1}\:{times}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{0} \\ $$$$\Rightarrow\frac{{dy}}{{dx}}={a}×\left(\begin{pmatrix}{{n}}\\{\mathrm{1}}\end{pmatrix}{x}^{{n}−\mathrm{1}} +\mathrm{0}\right)={anx}^{{n}−\mathrm{1}} . \\ $$$$ \\ $$

Commented by Filup last updated on 12/Dec/15

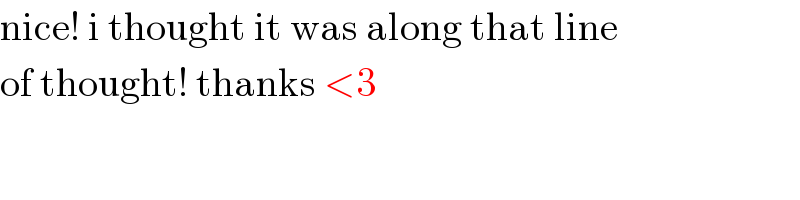
nice! i thought it was along that line of thought! thanks <3

$$\mathrm{nice}!\:\mathrm{i}\:\mathrm{thought}\:\mathrm{it}\:\mathrm{was}\:\mathrm{along}\:\mathrm{that}\:\mathrm{line} \\ $$$$\mathrm{of}\:\mathrm{thought}!\:\mathrm{thanks}\:<\mathrm{3} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com