
Previous in Relation and Functions Next in Relation and Functions
Question Number 33717 by prof Abdo imad last updated on 22/Apr/18
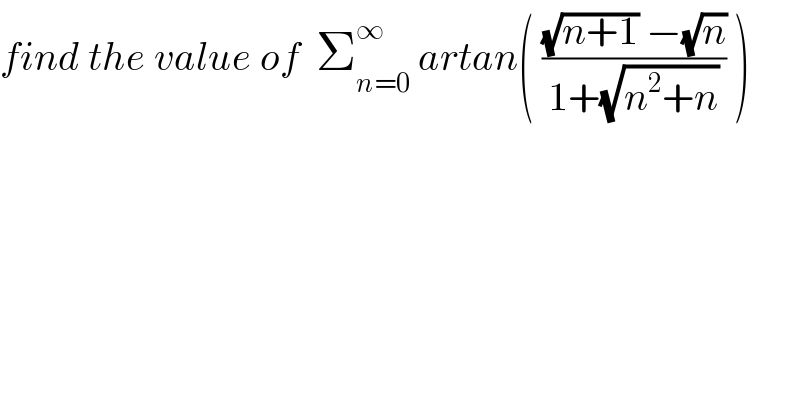
$${find}\:{the}\:{value}\:{of}\:\:\sum_{{n}=\mathrm{0}} ^{\infty} \:{artan}\left(\:\frac{\sqrt{{n}+\mathrm{1}}\:−\sqrt{{n}}}{\mathrm{1}+\sqrt{{n}^{\mathrm{2}} +{n}}}\:\right) \\ $$
Commented by prof Abdo imad last updated on 24/Apr/18
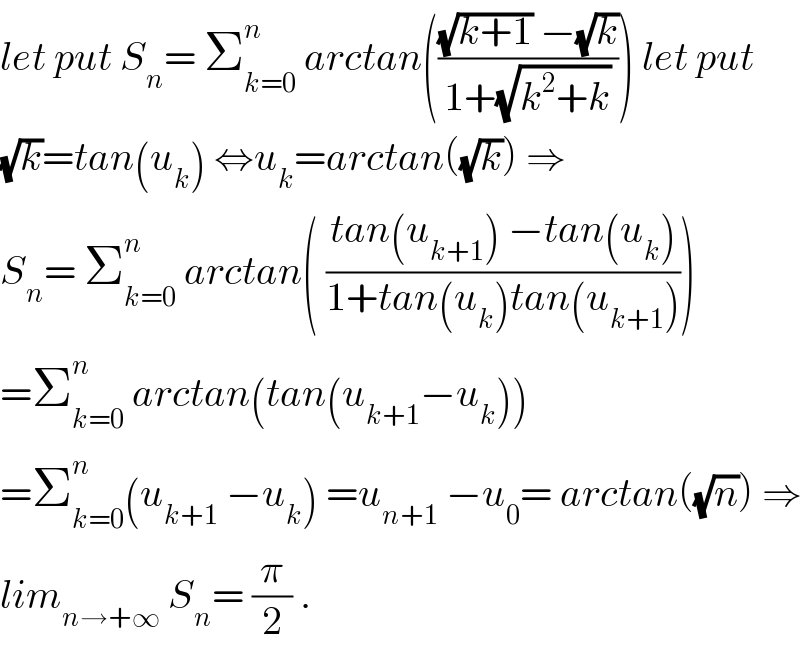
$${let}\:{put}\:{S}_{{n}} =\:\sum_{{k}=\mathrm{0}} ^{{n}} \:{arctan}\left(\frac{\sqrt{{k}+\mathrm{1}}\:−\sqrt{{k}}}{\mathrm{1}+\sqrt{{k}^{\mathrm{2}} +{k}}}\right)\:{let}\:{put} \\ $$$$\sqrt{{k}}={tan}\left({u}_{{k}} \right)\:\Leftrightarrow{u}_{{k}} ={arctan}\left(\sqrt{{k}}\right)\:\Rightarrow \\ $$$${S}_{{n}} =\:\sum_{{k}=\mathrm{0}} ^{{n}} \:{arctan}\left(\:\frac{{tan}\left({u}_{{k}+\mathrm{1}} \right)\:−{tan}\left({u}_{{k}} \right)}{\mathrm{1}+{tan}\left({u}_{{k}} \right){tan}\left({u}_{{k}+\mathrm{1}} \right)}\right) \\ $$$$=\sum_{{k}=\mathrm{0}} ^{{n}} \:{arctan}\left({tan}\left({u}_{{k}+\mathrm{1}} −{u}_{{k}} \right)\right) \\ $$$$=\sum_{{k}=\mathrm{0}} ^{{n}} \left({u}_{{k}+\mathrm{1}} \:−{u}_{{k}} \right)\:={u}_{{n}+\mathrm{1}} \:−{u}_{\mathrm{0}} =\:{arctan}\left(\sqrt{{n}}\right)\:\Rightarrow \\ $$$${lim}_{{n}\rightarrow+\infty} \:{S}_{{n}} =\:\frac{\pi}{\mathrm{2}}\:. \\ $$
Commented by prof Abdo imad last updated on 24/Apr/18

$${S}_{{n}} ={arctan}\left(\sqrt{{n}+\mathrm{1}}\right) \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 22/Apr/18

$$\underset{\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\left.{n}+\mathrm{1}\right)}\:−\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\left.{n}\right)}\right.\right. \\ $$$${T}_{{n}\:} =\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\left.{n}+\mathrm{1}\:\right)}\:\:−\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\left.{n}\right)}\right.\right. \\ $$$${T}_{\mathrm{0}} =\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\left.\mathrm{1}\right)}\:−\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{0}\right)\right. \\ $$$${T}_{\mathrm{1}} =\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\left.\mathrm{2}\right)}\:−\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{1}\right)\right. \\ $$$${so}\:{S}_{{n}} ={T}_{\mathrm{0}} \:+{T}_{\mathrm{1}} +.....+{T}_{{n}} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{{n}+\mathrm{1}}\:\right)−\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{0}\right) \\ $$$${when}\:{n}\:{tends}\:{to}\:{infinity}\:{the}\:{sum}\:{is} \\ $$$$\mathrm{tan}^{−\mathrm{1}} \left(\infty\right)\:−\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{0}\right) \\ $$$$=\coprod/\mathrm{2}\:−\mathrm{0} \\ $$$$=\coprod/\mathrm{2} \\ $$$$\coprod\:{this}\:{sign}\:{used}\:{as}\:{pie}\: \\ $$$$ \\ $$$$ \\ $$
