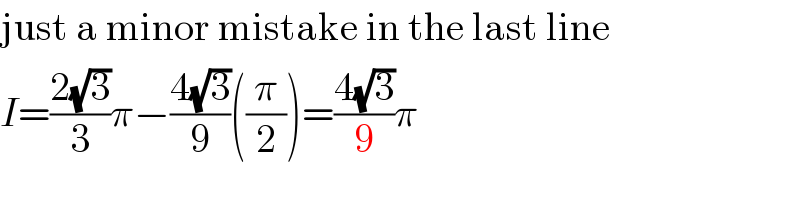Question Number 33736 by prof Abdo imad last updated on 23/Apr/18
$${find}\:{the}\:{value}\:{of}\:\:\int_{−\infty} ^{+\infty} \:\:\:\:\:\frac{{x}^{\mathrm{2}} }{\left(\mathrm{1}+{x}\:+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx} \\ $$
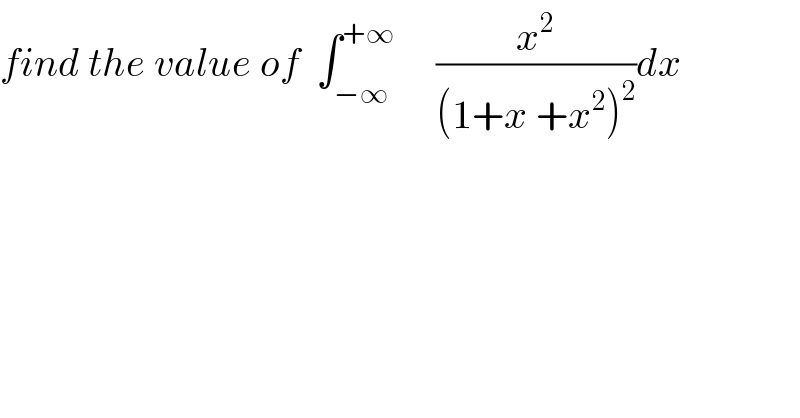
Commented by prof Abdo imad last updated on 23/Apr/18
$${let}\:\:{use}\:{residus}\:{theorem}\:{we}\:{have} \\ $$$${I}\:=\:\int_{−\infty} ^{+\infty} \:\:\:\:\frac{{x}^{\mathrm{2}} }{\left(\:\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{2}} }\:\:{ch}.\:{x}\:+\frac{\mathrm{1}}{\mathrm{2}}\:=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:{t} \\ $$$${give}\:\:\:{I}\:=\:\int_{−\infty} ^{+\infty} \:\:\:\:\:\frac{\left(\frac{\sqrt{\mathrm{3}}{t}}{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }{\left(\frac{\mathrm{3}}{\mathrm{4}}{t}^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{2}} }\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{dt} \\ $$$$=\frac{\mathrm{16}}{\mathrm{9}}\:.\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\:\int_{−\infty} ^{+\infty} \:\:\:\:\:\:\:\:\frac{\mathrm{3}{t}^{\mathrm{2}} \:−\mathrm{2}\sqrt{\mathrm{3}}\:{t}\:+\mathrm{1}}{\mathrm{4}\left(\:{t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }{dt} \\ $$$$=\:\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{9}}\:\int_{−\infty} ^{+\infty} \:\:\:\frac{\mathrm{3}{t}^{\mathrm{2}} \:−\mathrm{2}\sqrt{\mathrm{3}}\:{t}\:+\mathrm{1}}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:{dt}\:\:.{let}\:{consider} \\ $$$${the}\:{complex}\:{function}\:\varphi\left({z}\right)\:=\:\frac{\mathrm{3}{z}^{\mathrm{2}} \:−\mathrm{2}\sqrt{\mathrm{3}}\:{z}+\mathrm{1}}{\left({z}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${the}\:{poles}\:{of}\:\varphi\:{are}\:{i}\:{and}−{i}\:\left({doubles}\right) \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\:\pi\:{Res}\left(\varphi,{i}\right) \\ $$$${Res}\left(\varphi,{i}\right)\:={lim}_{{z}\rightarrow{i}} \:\:\:\frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{1}\right)!}\left(\left({z}−{i}\right)^{\mathrm{2}} \varphi\left({z}\right)\right)^{'} \\ $$$$={lim}_{{z}\rightarrow{i}} \left(\:\:\frac{\mathrm{3}{z}^{\mathrm{2}} \:−\mathrm{2}\sqrt{\mathrm{3}}\:{z}\:+\mathrm{1}}{\left({z}+{i}\right)^{\mathrm{2}} }\right)^{'} \\ $$$$={lim}_{{z}\rightarrow{i}} \:\:\frac{\left(\mathrm{6}{z}−\mathrm{2}\sqrt{\mathrm{3}}\right)\left({z}+{i}\right)^{\mathrm{2}} \:−\mathrm{2}\left({z}+{i}\right)\left(\mathrm{3}{z}^{\mathrm{2}} \:−\mathrm{2}\sqrt{\mathrm{3}}{z}\:+\mathrm{1}\right)}{\left({z}+{i}\right)^{\mathrm{4}} } \\ $$$$={lim}_{{z}\rightarrow{i}} \:\frac{\left(\mathrm{6}{z}\:−\mathrm{2}\sqrt{\mathrm{3}}\right)\left({z}+{i}\right)\:−\mathrm{2}\left(\mathrm{3}{z}^{\mathrm{2}} \:−\mathrm{2}\sqrt{\mathrm{3}}\:{z}\:+\mathrm{1}\right)}{\left({z}+{i}\right)^{\mathrm{3}} } \\ $$$$=\:\frac{\left(\mathrm{6}{i}\:−\mathrm{2}\sqrt{\mathrm{3}}\right)\left(\mathrm{2}{i}\right)\:−\mathrm{2}\left(\:\mathrm{3}{i}^{\mathrm{2}} \:−\mathrm{2}\sqrt{\mathrm{3}}\:{i}\:+\mathrm{1}\right)}{\left(\mathrm{2}{i}\right)^{\mathrm{3}} } \\ $$$$=\frac{−\mathrm{12}\:−\mathrm{4}\sqrt{\mathrm{3}}\:{i}\:+\mathrm{6}\:\:\mathrm{4}\sqrt{\mathrm{3}}{i}\:−\mathrm{2}}{−\mathrm{8}{i}}\:=\:\frac{−\mathrm{8}}{−\mathrm{8}{i}}\:=\:\frac{\mathrm{1}}{{i}}\:\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left(\frac{\mathrm{1}}{{i}}\right)=\mathrm{2}\pi\:\Rightarrow \\ $$$${I}=\:\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{9}}\:.\left(\mathrm{2}\pi\right)\:=\frac{\mathrm{4}\pi\sqrt{\mathrm{3}}}{\mathrm{9}} \\ $$$$\bigstar\:{I}\:=\frac{\mathrm{4}\pi\sqrt{\mathrm{3}}}{\mathrm{9}}\:\bigstar\: \\ $$$$ \\ $$$$ \\ $$
Answered by MJS last updated on 28/Apr/18
![Ostrogradski′s Method: ∫((P(x))/(Q(x)))dx=((P_1 (x))/(Q_1 (x)))+∫((P_2 (x))/(Q_2 (x)))dx Q_1 (x)=gcd(Q(x);Q′(x)) Q_2 (x)=((Q(x))/(Q_1 (x))) P(x)=x^2 Q(x)=(x^2 +x+1)^2 Q′(x)=2(2x+1)(x^2 +x+1) gcd(Q(x);Q′(x))=(x^2 +x+1)=Q_1 (x)=Q_2 (x) to get P_1 (x)=k_1 x+k_2 , P_2 (x)=k_3 x+k_4 ((P(x))/(Q(x)))=(((P_1 (x))/(Q_1 (x))))^′ +((P_2 (x))/(Q_2 (x))) (x^2 /((x^2 +x+1)^2 ))=((k_1 (x^2 +x+1)−(k_1 x+k_2 )(2x+1))/((x^2 +x+1)^2 ))+((k_3 x+k_4 )/(x^2 +x+1)) [multiplicate with (x^2 +x+1)^2 ] x^2 =k_3 x^3 +(−k_1 +k_3 +k_4 )x^2 +(−2k_2 +k_3 +k_4 )x+(k_1 −k_2 +k_4 ) k_3 =0 −k_1 +k_3 +k_4 =1 −2k_2 +k_3 +k_4 =0 k_1 −k_2 +k_4 =0 k_1 =−(1/3); k_2 =(1/3); k_3 =0; k_4 =(2/3) P_1 (x)=−((x−1)/3); P_2 (x)=(2/3) ∫((P(x))/(Q(x)))dx=((P_1 (x))/(Q_1 (x)))+∫((P_2 (x))/(Q_2 (x)))dx= =−((x−1)/(3(x^2 +x+1)))+(2/3)∫(1/(x^2 +x+1))dx (1/(x^2 +x+1))=(1/((x+(1/2))^2 +(3/4)))=(4/((2x+1)^2 +3)) (8/3)∫(1/((2x+1)^2 +3))dx= u=((2x+1)/(√3)) → dx=((√3)/2)du x=((u(√3)−1)/2) (8/3)∫((√3)/(2(3u^2 +3)))du=((4(√3))/9)∫(1/(u^2 +1))du= =((4(√3))/9)arctan u =((4(√3))/9)arctan (((√3)/3)(2x+1)) ∫(x^2 /((x^2 +x+1)^2 ))dx=((4(√3))/9)arctan (((√3)/3)(2x+1))−((x−1)/(3(x^2 +x+1)))+C ∫_(−∞) ^∞ (x^2 /((x^2 +x+1)^2 ))dx=((4(√3))/9)π](Q33751.png)
$$\mathrm{O}{s}\mathrm{trogradski}'\mathrm{s}\:\mathrm{Method}: \\ $$$$\int\frac{{P}\left({x}\right)}{{Q}\left({x}\right)}{dx}=\frac{{P}_{\mathrm{1}} \left({x}\right)}{{Q}_{\mathrm{1}} \left({x}\right)}+\int\frac{{P}_{\mathrm{2}} \left({x}\right)}{{Q}_{\mathrm{2}} \left({x}\right)}{dx} \\ $$$${Q}_{\mathrm{1}} \left({x}\right)={gcd}\left({Q}\left({x}\right);{Q}'\left({x}\right)\right) \\ $$$${Q}_{\mathrm{2}} \left({x}\right)=\frac{{Q}\left({x}\right)}{{Q}_{\mathrm{1}} \left({x}\right)} \\ $$$$ \\ $$$${P}\left({x}\right)={x}^{\mathrm{2}} \\ $$$${Q}\left({x}\right)=\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$${Q}'\left({x}\right)=\mathrm{2}\left(\mathrm{2}{x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right) \\ $$$${gcd}\left({Q}\left({x}\right);{Q}'\left({x}\right)\right)=\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)={Q}_{\mathrm{1}} \left({x}\right)={Q}_{\mathrm{2}} \left({x}\right) \\ $$$$ \\ $$$$\mathrm{to}\:\mathrm{get}\:{P}_{\mathrm{1}} \left({x}\right)={k}_{\mathrm{1}} {x}+{k}_{\mathrm{2}} ,\:{P}_{\mathrm{2}} \left({x}\right)={k}_{\mathrm{3}} {x}+{k}_{\mathrm{4}} \\ $$$$\frac{{P}\left({x}\right)}{{Q}\left({x}\right)}=\left(\frac{{P}_{\mathrm{1}} \left({x}\right)}{{Q}_{\mathrm{1}} \left({x}\right)}\right)^{'} +\frac{{P}_{\mathrm{2}} \left({x}\right)}{{Q}_{\mathrm{2}} \left({x}\right)} \\ $$$$\frac{{x}^{\mathrm{2}} }{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{2}} }=\frac{{k}_{\mathrm{1}} \left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)−\left({k}_{\mathrm{1}} {x}+{k}_{\mathrm{2}} \right)\left(\mathrm{2}{x}+\mathrm{1}\right)}{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{{k}_{\mathrm{3}} {x}+{k}_{\mathrm{4}} }{{x}^{\mathrm{2}} +{x}+\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\left[\mathrm{multiplicate}\:\mathrm{with}\:\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{2}} \right] \\ $$$${x}^{\mathrm{2}} ={k}_{\mathrm{3}} {x}^{\mathrm{3}} +\left(−{k}_{\mathrm{1}} +{k}_{\mathrm{3}} +{k}_{\mathrm{4}} \right){x}^{\mathrm{2}} +\left(−\mathrm{2}{k}_{\mathrm{2}} +{k}_{\mathrm{3}} +{k}_{\mathrm{4}} \right){x}+\left({k}_{\mathrm{1}} −{k}_{\mathrm{2}} +{k}_{\mathrm{4}} \right) \\ $$$${k}_{\mathrm{3}} =\mathrm{0} \\ $$$$−{k}_{\mathrm{1}} +{k}_{\mathrm{3}} +{k}_{\mathrm{4}} =\mathrm{1} \\ $$$$−\mathrm{2}{k}_{\mathrm{2}} +{k}_{\mathrm{3}} +{k}_{\mathrm{4}} =\mathrm{0} \\ $$$${k}_{\mathrm{1}} −{k}_{\mathrm{2}} +{k}_{\mathrm{4}} =\mathrm{0} \\ $$$${k}_{\mathrm{1}} =−\frac{\mathrm{1}}{\mathrm{3}};\:{k}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{3}};\:{k}_{\mathrm{3}} =\mathrm{0};\:{k}_{\mathrm{4}} =\frac{\mathrm{2}}{\mathrm{3}} \\ $$$${P}_{\mathrm{1}} \left({x}\right)=−\frac{{x}−\mathrm{1}}{\mathrm{3}};\:{P}_{\mathrm{2}} \left({x}\right)=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$ \\ $$$$\int\frac{{P}\left({x}\right)}{{Q}\left({x}\right)}{dx}=\frac{{P}_{\mathrm{1}} \left({x}\right)}{{Q}_{\mathrm{1}} \left({x}\right)}+\int\frac{{P}_{\mathrm{2}} \left({x}\right)}{{Q}_{\mathrm{2}} \left({x}\right)}{dx}= \\ $$$$=−\frac{{x}−\mathrm{1}}{\mathrm{3}\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)}+\frac{\mathrm{2}}{\mathrm{3}}\int\frac{\mathrm{1}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{dx} \\ $$$$ \\ $$$$\frac{\mathrm{1}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}=\frac{\mathrm{1}}{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}}=\frac{\mathrm{4}}{\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{3}} \\ $$$$ \\ $$$$\frac{\mathrm{8}}{\mathrm{3}}\int\frac{\mathrm{1}}{\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{3}}{dx}= \\ $$$$\:\:\:\:\:\:\:\:\:\:{u}=\frac{\mathrm{2}{x}+\mathrm{1}}{\sqrt{\mathrm{3}}}\:\rightarrow\:{dx}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{du} \\ $$$$\:\:\:\:\:\:\:\:\:\:{x}=\frac{{u}\sqrt{\mathrm{3}}−\mathrm{1}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{8}}{\mathrm{3}}\int\frac{\sqrt{\mathrm{3}}}{\mathrm{2}\left(\mathrm{3}{u}^{\mathrm{2}} +\mathrm{3}\right)}{du}=\frac{\mathrm{4}\sqrt{\mathrm{3}}}{\mathrm{9}}\int\frac{\mathrm{1}}{{u}^{\mathrm{2}} +\mathrm{1}}{du}= \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{4}\sqrt{\mathrm{3}}}{\mathrm{9}}\mathrm{arctan}\:{u} \\ $$$$=\frac{\mathrm{4}\sqrt{\mathrm{3}}}{\mathrm{9}}\mathrm{arctan}\:\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\left(\mathrm{2}{x}+\mathrm{1}\right)\right) \\ $$$$ \\ $$$$\int\frac{{x}^{\mathrm{2}} }{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{2}} }{dx}=\frac{\mathrm{4}\sqrt{\mathrm{3}}}{\mathrm{9}}\mathrm{arctan}\:\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\left(\mathrm{2}{x}+\mathrm{1}\right)\right)−\frac{{x}−\mathrm{1}}{\mathrm{3}\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)}+{C} \\ $$$$ \\ $$$$\underset{−\infty} {\overset{\infty} {\int}}\frac{{x}^{\mathrm{2}} }{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{2}} }{dx}=\frac{\mathrm{4}\sqrt{\mathrm{3}}}{\mathrm{9}}\pi \\ $$
Commented by prof Abdo imad last updated on 23/Apr/18
$${thank}\:{you}\:{sir}\:{for}\:{this}\:{new}\:{method}... \\ $$
Answered by sma3l2996 last updated on 23/Apr/18
![I=∫_(−∞) ^(+∞) (x^2 /((1+x+x^2 )^2 ))dx=∫_(−∞) ^(+∞) ((x^2 +x+1−(x+1))/((x^2 +x+1)^2 ))dx =∫_(−∞) ^(+∞) (1/(x^2 +x+1))dx−(1/2)∫_(−∞) ^(+∞) ((2x+2)/((x^2 +x+1)^2 ))dx =∫_(−∞) ^(+∞) (dx/((x+(1/2))^2 +(3/4)))−(1/2)∫_(−∞) ^(+∞) ((2x+1)/((x^2 +x+1)^2 ))dx−(1/2)∫_(−∞) ^(+∞) (dx/(((x+(1/2))^2 +(3/4))^2 )) =(4/3)∫_(−∞) ^(+∞) (dx/((((2x+1)/(√3)))^2 +1))+(1/2)[(1/(x^2 +x+1))]_(−∞) ^(+∞) −(8/9)∫_(−∞) ^(+∞) (dx/(((((2x+1)/(√3)))^2 +1)^2 )) let t=((2x+1)/(√3))⇒dx=((√3)/2)dt so I=((2(√3))/3)∫_(−∞) ^(+∞) (dt/(t^2 +1))−((4(√3))/9)∫_(−∞) ^(+∞) (dt/((t^2 +1)^2 )) let t=tanu⇒dt=(1+tan^2 u)du I=((2(√3))/3)[tan^(−1) (t)]_(−∞) ^(+∞) −((4(√3))/9)∫_(−π/2) ^(π/2) (du/(1+tan^2 u)) =((2(√3))/3)π−((4(√3))/9)∫_(−π/2) ^(π/2) cos^2 (u)du ∫_(−π/2) ^(π/2) cos^2 (u)du=(1/2)∫_(−π/2) ^(π/2) (cos(2u)+1)du=(1/2)[(1/2)sin(2x)+x]_(−π/2) ^(π/2) =(π/2) I=((2(√3))/3)π−((4(√3))/9)((π/2))=((4(√3))/3)π](Q33746.png)
$${I}=\int_{−\infty} ^{+\infty} \frac{{x}^{\mathrm{2}} }{\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx}=\int_{−\infty} ^{+\infty} \frac{{x}^{\mathrm{2}} +{x}+\mathrm{1}−\left({x}+\mathrm{1}\right)}{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$$$=\int_{−\infty} ^{+\infty} \frac{\mathrm{1}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{dx}−\frac{\mathrm{1}}{\mathrm{2}}\int_{−\infty} ^{+\infty} \frac{\mathrm{2}{x}+\mathrm{2}}{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$$$=\int_{−\infty} ^{+\infty} \frac{{dx}}{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}}−\frac{\mathrm{1}}{\mathrm{2}}\int_{−\infty} ^{+\infty} \frac{\mathrm{2}{x}+\mathrm{1}}{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{2}} }{dx}−\frac{\mathrm{1}}{\mathrm{2}}\int_{−\infty} ^{+\infty} \frac{{dx}}{\left(\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{4}}{\mathrm{3}}\int_{−\infty} ^{+\infty} \frac{{dx}}{\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} +\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{1}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\right]_{−\infty} ^{+\infty} −\frac{\mathrm{8}}{\mathrm{9}}\int_{−\infty} ^{+\infty} \frac{{dx}}{\left(\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${let}\:\:{t}=\frac{\mathrm{2}{x}+\mathrm{1}}{\sqrt{\mathrm{3}}}\Rightarrow{dx}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{dt} \\ $$$${so}\:\:{I}=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\int_{−\infty} ^{+\infty} \frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}−\frac{\mathrm{4}\sqrt{\mathrm{3}}}{\mathrm{9}}\int_{−\infty} ^{+\infty} \frac{{dt}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${let}\:\:{t}={tanu}\Rightarrow{dt}=\left(\mathrm{1}+{tan}^{\mathrm{2}} {u}\right){du} \\ $$$${I}=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\left[{tan}^{−\mathrm{1}} \left({t}\right)\right]_{−\infty} ^{+\infty} −\frac{\mathrm{4}\sqrt{\mathrm{3}}}{\mathrm{9}}\int_{−\pi/\mathrm{2}} ^{\pi/\mathrm{2}} \frac{{du}}{\mathrm{1}+{tan}^{\mathrm{2}} {u}} \\ $$$$=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\pi−\frac{\mathrm{4}\sqrt{\mathrm{3}}}{\mathrm{9}}\int_{−\pi/\mathrm{2}} ^{\pi/\mathrm{2}} {cos}^{\mathrm{2}} \left({u}\right){du} \\ $$$$\int_{−\pi/\mathrm{2}} ^{\pi/\mathrm{2}} {cos}^{\mathrm{2}} \left({u}\right){du}=\frac{\mathrm{1}}{\mathrm{2}}\int_{−\pi/\mathrm{2}} ^{\pi/\mathrm{2}} \left({cos}\left(\mathrm{2}{u}\right)+\mathrm{1}\right){du}=\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{1}}{\mathrm{2}}{sin}\left(\mathrm{2}{x}\right)+{x}\right]_{−\pi/\mathrm{2}} ^{\pi/\mathrm{2}} \\ $$$$=\frac{\pi}{\mathrm{2}} \\ $$$${I}=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\pi−\frac{\mathrm{4}\sqrt{\mathrm{3}}}{\mathrm{9}}\left(\frac{\pi}{\mathrm{2}}\right)=\frac{\mathrm{4}\sqrt{\mathrm{3}}}{\mathrm{3}}\pi \\ $$
Commented by MJS last updated on 23/Apr/18
$$\mathrm{just}\:\mathrm{a}\:\mathrm{minor}\:\mathrm{mistake}\:\mathrm{in}\:\mathrm{the}\:\mathrm{last}\:\mathrm{line} \\ $$$${I}=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\pi−\frac{\mathrm{4}\sqrt{\mathrm{3}}}{\mathrm{9}}\left(\frac{\pi}{\mathrm{2}}\right)=\frac{\mathrm{4}\sqrt{\mathrm{3}}}{\mathrm{9}}\pi \\ $$