Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 33737 by prof Abdo imad last updated on 23/Apr/18

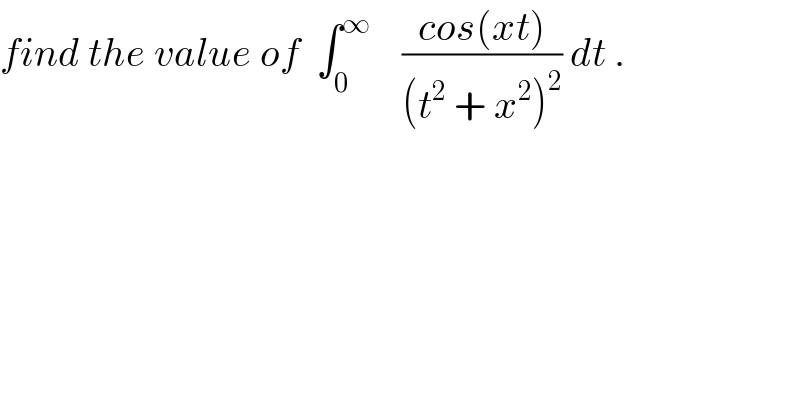
find the value of ∫_0 ^∞ ((cos(xt))/((t^2 + x^2 )^2 )) dt .

$${find}\:{the}\:{value}\:{of}\:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{cos}\left({xt}\right)}{\left({t}^{\mathrm{2}} \:+\:{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:{dt}\:. \\ $$

Commented by prof Abdo imad last updated on 23/Apr/18

let put f(x)= ∫_0 ^∞ ((cos(xt))/((t^2 +x^2 )^2 ))dt f(x)=(1/2) ∫_(−∞) ^(+∞) ((cos(xt))/((t^2 +x^2 )^2 ))dt ⇒ 2f(x)= Re( ∫_(−∞) ^(+∞) (e^(ixt) /((t^2 +x^2 )^2 ))dt) let introduce the complex function ϕ(z) = (e^(ixz) /((z^2 +x^2 )^2 )) the poles of ϕ are ix ,−ix(doubles) case 1 x>0 ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ Res(ϕ,ix) Res(ϕ,ix) = lim_(z→ix) (1/((2−1)!))( (z−ix)^2 ϕ(z))^′ =lim_(z→ix) ( (e^(ixz) /((z+ix)^2 )))^′ =lim_(z→ix) ( ((ix e^(ixz) ( z+ix)^2 −2(z+ix)e^(ixz) )/((z+ix)^4 ))) =lim_(z→ix) ((ixe^(ixz) (z+ix) −2 e^(ixz) )/((z+ix)^3 )) =(( ix e^(−x^2 ) (2ix) −2 e^(−x^2 ) )/((2ix)^3 )) =((−2x^2 e^(−x^2 ) −2e^(−x^2 ) )/(−8i x^3 )) = (((x^2 +1)e^(−x^2 ) )/(4ix^3 )) ⇒2f(x)=2iπ (((x^2 +1)e^(−x^2 ) )/(4ix^3 )) ⇒ f(x)=((iπ)/4)( 1+x^2 )e^(−x^2 ) .

$${let}\:{put}\:{f}\left({x}\right)=\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{cos}\left({xt}\right)}{\left({t}^{\mathrm{2}} \:+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{dt} \\ $$$${f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{−\infty} ^{+\infty} \:\:\:\:\frac{{cos}\left({xt}\right)}{\left({t}^{\mathrm{2}} \:+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{dt}\:\Rightarrow \\ $$$$\mathrm{2}{f}\left({x}\right)=\:{Re}\left(\:\:\int_{−\infty} ^{+\infty} \:\:\frac{{e}^{{ixt}} }{\left({t}^{\mathrm{2}} \:+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{dt}\right)\:{let}\:{introduce} \\ $$$${the}\:{complex}\:{function}\:\varphi\left({z}\right)\:=\:\frac{{e}^{{ixz}} }{\left({z}^{\mathrm{2}} \:+{x}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$${the}\:{poles}\:{of}\:\varphi\:{are}\:{ix}\:,−{ix}\left({doubles}\right) \\ $$$${case}\:\mathrm{1}\:\:{x}>\mathrm{0} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:{Res}\left(\varphi,{ix}\right) \\ $$$${Res}\left(\varphi,{ix}\right)\:=\:{lim}_{{z}\rightarrow{ix}} \:\frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{1}\right)!}\left(\:\left({z}−{ix}\right)^{\mathrm{2}} \varphi\left({z}\right)\right)^{'} \\ $$$$={lim}_{{z}\rightarrow{ix}} \left(\:\:\frac{{e}^{{ixz}} }{\left({z}+{ix}\right)^{\mathrm{2}} }\right)^{'} \\ $$$$={lim}_{{z}\rightarrow{ix}} \left(\:\:\:\frac{{ix}\:{e}^{{ixz}} \left(\:{z}+{ix}\right)^{\mathrm{2}} \:\:−\mathrm{2}\left({z}+{ix}\right){e}^{{ixz}} }{\left({z}+{ix}\right)^{\mathrm{4}} }\right) \\ $$$$={lim}_{{z}\rightarrow{ix}} \:\:\:\frac{{ixe}^{{ixz}} \left({z}+{ix}\right)\:−\mathrm{2}\:{e}^{{ixz}} }{\left({z}+{ix}\right)^{\mathrm{3}} } \\ $$$$=\frac{\:{ix}\:{e}^{−{x}^{\mathrm{2}} } \left(\mathrm{2}{ix}\right)\:−\mathrm{2}\:{e}^{−{x}^{\mathrm{2}} } }{\left(\mathrm{2}{ix}\right)^{\mathrm{3}} }\:=\frac{−\mathrm{2}{x}^{\mathrm{2}} \:{e}^{−{x}^{\mathrm{2}} } −\mathrm{2}{e}^{−{x}^{\mathrm{2}} } }{−\mathrm{8}{i}\:{x}^{\mathrm{3}} }\: \\ $$$$=\:\frac{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right){e}^{−{x}^{\mathrm{2}} } }{\mathrm{4}{ix}^{\mathrm{3}} }\:\Rightarrow\mathrm{2}{f}\left({x}\right)=\mathrm{2}{i}\pi\:\frac{\left({x}^{\mathrm{2}} +\mathrm{1}\right){e}^{−{x}^{\mathrm{2}} } }{\mathrm{4}{ix}^{\mathrm{3}} } \\ $$$$\Rightarrow\:{f}\left({x}\right)=\frac{{i}\pi}{\mathrm{4}}\left(\:\mathrm{1}+{x}^{\mathrm{2}} \right){e}^{−{x}^{\mathrm{2}} } \:. \\ $$

Commented by prof Abdo imad last updated on 23/Apr/18

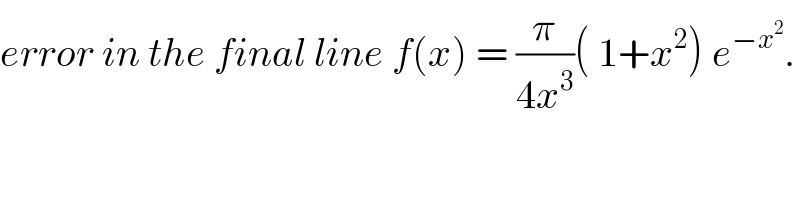
error in the final line f(x) = (π/(4x^3 ))( 1+x^2 ) e^(−x^2 ) .

$${error}\:{in}\:{the}\:{final}\:{line}\:{f}\left({x}\right)\:=\:\frac{\pi}{\mathrm{4}{x}^{\mathrm{3}} }\left(\:\mathrm{1}+{x}^{\mathrm{2}} \right)\:{e}^{−{x}^{\mathrm{2}} } . \\ $$

Commented by caravan msup abdo. last updated on 24/Apr/18

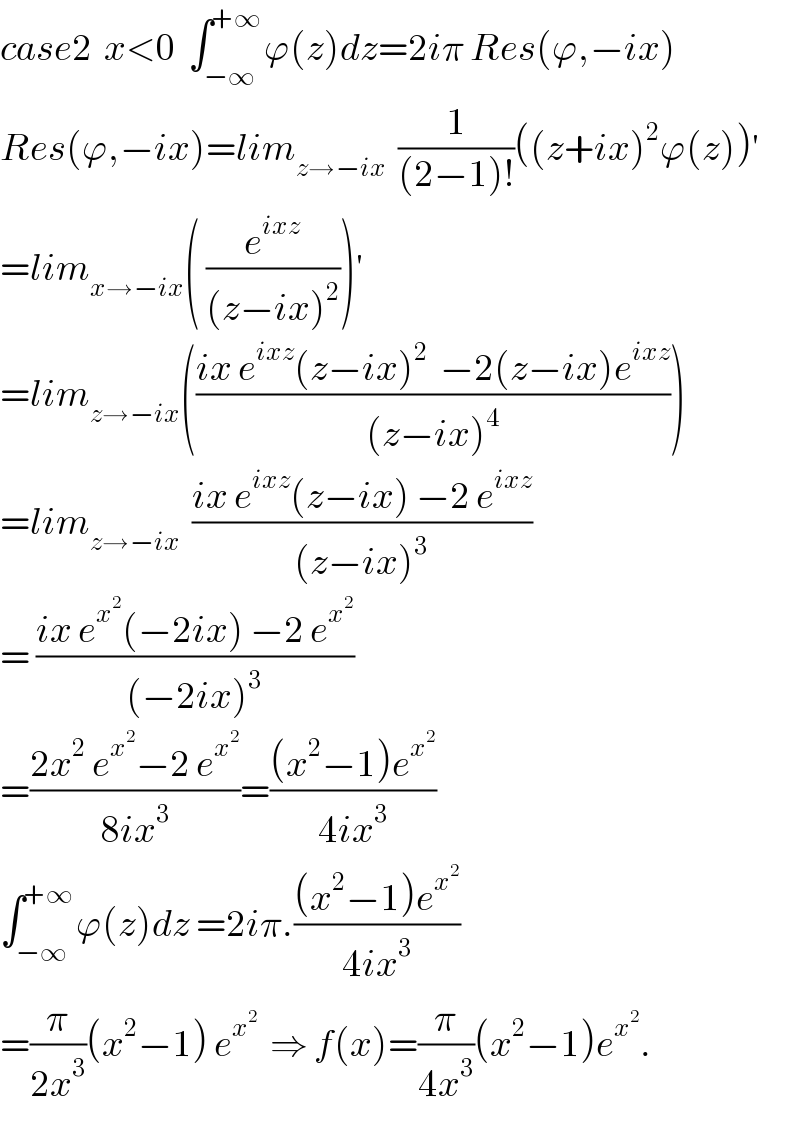
case2 x<0 ∫_(−∞) ^(+∞) ϕ(z)dz=2iπ Res(ϕ,−ix) Res(ϕ,−ix)=lim_(z→−ix) (1/((2−1)!))((z+ix)^2 ϕ(z))^′ =lim_(x→−ix) ( (e^(ixz) /((z−ix)^2 )))^′ =lim_(z→−ix) (((ix e^(ixz) (z−ix)^2 −2(z−ix)e^(ixz) )/((z−ix)^4 ))) =lim_(z→−ix) ((ix e^(ixz) (z−ix) −2 e^(ixz) )/((z−ix)^3 )) = ((ix e^x^2 (−2ix) −2 e^x^2 )/((−2ix)^3 )) =((2x^2 e^x^2 −2 e^x^2 )/(8ix^3 ))=(((x^2 −1)e^x^2 )/(4ix^3 )) ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ.(((x^2 −1)e^x^2 )/(4ix^3 )) =(π/(2x^3 ))(x^2 −1) e^x^2 ⇒ f(x)=(π/(4x^3 ))(x^2 −1)e^x^2 .

$${case}\mathrm{2}\:\:{x}<\mathrm{0}\:\:\int_{−\infty} ^{+\infty} \varphi\left({z}\right){dz}=\mathrm{2}{i}\pi\:{Res}\left(\varphi,−{ix}\right) \\ $$$${Res}\left(\varphi,−{ix}\right)={lim}_{{z}\rightarrow−{ix}} \:\:\frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{1}\right)!}\left(\left({z}+{ix}\right)^{\mathrm{2}} \varphi\left({z}\right)\right)^{'} \\ $$$$={lim}_{{x}\rightarrow−{ix}} \left(\:\frac{{e}^{{ixz}} }{\left({z}−{ix}\right)^{\mathrm{2}} }\right)^{'} \\ $$$$={lim}_{{z}\rightarrow−{ix}} \left(\frac{{ix}\:{e}^{{ixz}} \left({z}−{ix}\right)^{\mathrm{2}} \:\:−\mathrm{2}\left({z}−{ix}\right){e}^{{ixz}} }{\left({z}−{ix}\right)^{\mathrm{4}} }\right) \\ $$$$={lim}_{{z}\rightarrow−{ix}} \:\:\frac{{ix}\:{e}^{{ixz}} \left({z}−{ix}\right)\:−\mathrm{2}\:{e}^{{ixz}} }{\left({z}−{ix}\right)^{\mathrm{3}} } \\ $$$$=\:\frac{{ix}\:{e}^{{x}^{\mathrm{2}} } \left(−\mathrm{2}{ix}\right)\:−\mathrm{2}\:{e}^{{x}^{\mathrm{2}} } }{\left(−\mathrm{2}{ix}\right)^{\mathrm{3}} } \\ $$$$=\frac{\mathrm{2}{x}^{\mathrm{2}} \:{e}^{{x}^{\mathrm{2}} } −\mathrm{2}\:{e}^{{x}^{\mathrm{2}} } }{\mathrm{8}{ix}^{\mathrm{3}} }=\frac{\left({x}^{\mathrm{2}} −\mathrm{1}\right){e}^{{x}^{\mathrm{2}} } }{\mathrm{4}{ix}^{\mathrm{3}} } \\ $$$$\int_{−\infty} ^{+\infty} \varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi.\frac{\left({x}^{\mathrm{2}} −\mathrm{1}\right){e}^{{x}^{\mathrm{2}} } }{\mathrm{4}{ix}^{\mathrm{3}} } \\ $$$$=\frac{\pi}{\mathrm{2}{x}^{\mathrm{3}} }\left({x}^{\mathrm{2}} −\mathrm{1}\right)\:{e}^{{x}^{\mathrm{2}} } \:\:\Rightarrow\:{f}\left({x}\right)=\frac{\pi}{\mathrm{4}{x}^{\mathrm{3}} }\left({x}^{\mathrm{2}} −\mathrm{1}\right){e}^{{x}^{\mathrm{2}} } . \\ $$

Answered by sma3l2996 last updated on 23/Apr/18

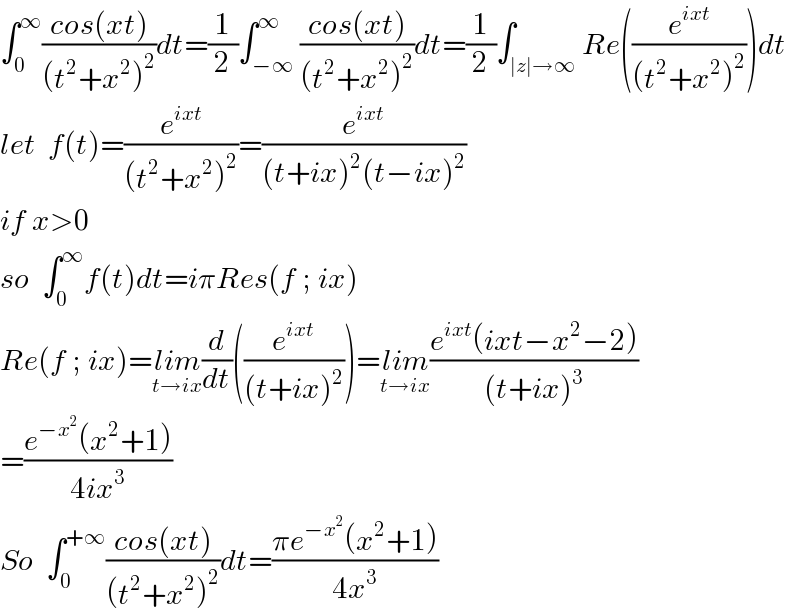
∫_0 ^∞ ((cos(xt))/((t^2 +x^2 )^2 ))dt=(1/2)∫_(−∞) ^∞ ((cos(xt))/((t^2 +x^2 )^2 ))dt=(1/2)∫_(∣z∣→∞) Re((e^(ixt) /((t^2 +x^2 )^2 )))dt let f(t)=(e^(ixt) /((t^2 +x^2 )^2 ))=(e^(ixt) /((t+ix)^2 (t−ix)^2 )) if x>0 so ∫_0 ^∞ f(t)dt=iπRes(f ; ix) Re(f ; ix)=lim_(t→ix) (d/dt)((e^(ixt) /((t+ix)^2 )))=lim_(t→ix) ((e^(ixt) (ixt−x^2 −2))/((t+ix)^3 )) =((e^(−x^2 ) (x^2 +1))/(4ix^3 )) So ∫_0 ^(+∞) ((cos(xt))/((t^2 +x^2 )^2 ))dt=((πe^(−x^2 ) (x^2 +1))/(4x^3 ))

$$\int_{\mathrm{0}} ^{\infty} \frac{{cos}\left({xt}\right)}{\left({t}^{\mathrm{2}} +{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{dt}=\frac{\mathrm{1}}{\mathrm{2}}\int_{−\infty} ^{\infty} \frac{{cos}\left({xt}\right)}{\left({t}^{\mathrm{2}} +{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{dt}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mid{z}\mid\rightarrow\infty} {Re}\left(\frac{{e}^{{ixt}} }{\left({t}^{\mathrm{2}} +{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\right){dt} \\ $$$${let}\:\:{f}\left({t}\right)=\frac{{e}^{{ixt}} }{\left({t}^{\mathrm{2}} +{x}^{\mathrm{2}} \right)^{\mathrm{2}} }=\frac{{e}^{{ixt}} }{\left({t}+{ix}\right)^{\mathrm{2}} \left({t}−{ix}\right)^{\mathrm{2}} } \\ $$$${if}\:{x}>\mathrm{0} \\ $$$${so}\:\:\int_{\mathrm{0}} ^{\infty} {f}\left({t}\right){dt}={i}\pi{Res}\left({f}\:;\:{ix}\right)\: \\ $$$${Re}\left({f}\:;\:{ix}\right)=\underset{{t}\rightarrow{ix}} {{lim}}\frac{{d}}{{dt}}\left(\frac{{e}^{{ixt}} }{\left({t}+{ix}\right)^{\mathrm{2}} }\right)=\underset{{t}\rightarrow{ix}} {{lim}}\frac{{e}^{{ixt}} \left({ixt}−{x}^{\mathrm{2}} −\mathrm{2}\right)}{\left({t}+{ix}\right)^{\mathrm{3}} } \\ $$$$=\frac{{e}^{−{x}^{\mathrm{2}} } \left({x}^{\mathrm{2}} +\mathrm{1}\right)}{\mathrm{4}{ix}^{\mathrm{3}} } \\ $$$${So}\:\:\int_{\mathrm{0}} ^{+\infty} \frac{{cos}\left({xt}\right)}{\left({t}^{\mathrm{2}} +{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{dt}=\frac{\pi{e}^{−{x}^{\mathrm{2}} } \left({x}^{\mathrm{2}} +\mathrm{1}\right)}{\mathrm{4}{x}^{\mathrm{3}} } \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com