
Question and Answers Forum
Question Number 33744 by prof Abdo imad last updated on 23/Apr/18
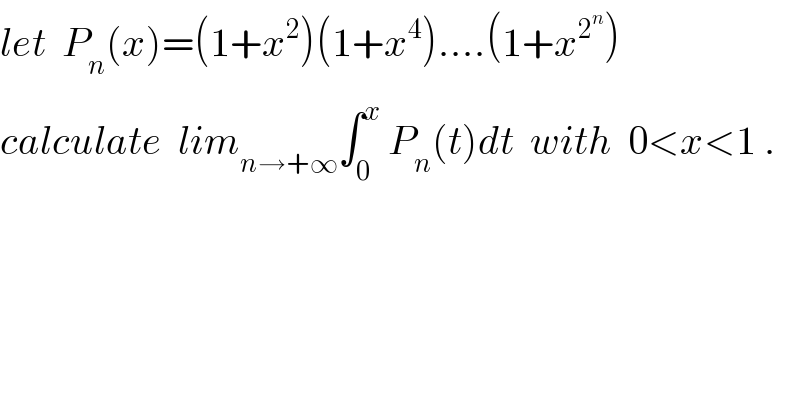
Commented byprof Abdo imad last updated on 25/Apr/18
![we have proved that P_n (t) = ((1−t^2^(n+1) )/(1−t^2 )) ⇒ ∫_0 ^x P_n (t)dt = ∫_0 ^x ((1−t^2^(n+1) )/(1−t^2 ))dt = ∫_0 ^x (dt/(1−t^2 )) −∫_0 ^x (t^2^(n+1) /(1−t^2 )) dt but lim_(n→+∞) ∫_0 ^x (t^2^(n+1) /(1−t^2 )) dt =0 because 0≤ ⇒t≤x<1 ⇒ lim_(n→+∞) ∫_0 ^x P_n (t)dt = ∫_0 ^x (dt/(1−t^2 )) =(1/2) ∫_0 ^x ( (1/(1−t)) +(1/(1+t)))dt =[(1/2)ln∣((1+t)/(1−t))∣]_0 ^c =(1/2) ln∣ ((1+x)/(1−x))∣ .](Q33806.png)
| ||
Question and Answers Forum | ||
Question Number 33744 by prof Abdo imad last updated on 23/Apr/18 | ||
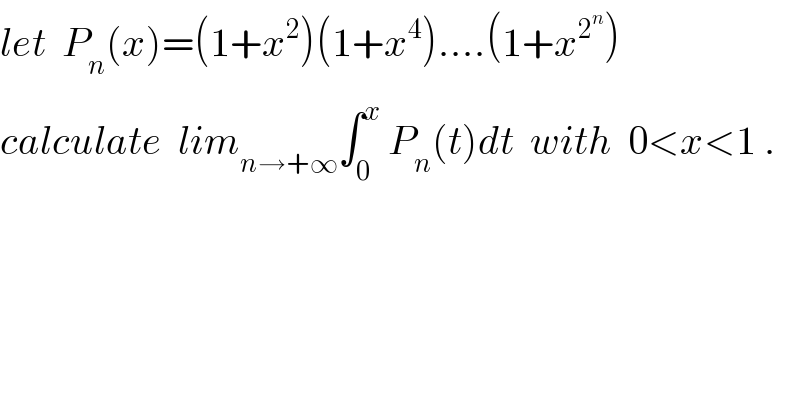 | ||
Commented byprof Abdo imad last updated on 25/Apr/18 | ||
![we have proved that P_n (t) = ((1−t^2^(n+1) )/(1−t^2 )) ⇒ ∫_0 ^x P_n (t)dt = ∫_0 ^x ((1−t^2^(n+1) )/(1−t^2 ))dt = ∫_0 ^x (dt/(1−t^2 )) −∫_0 ^x (t^2^(n+1) /(1−t^2 )) dt but lim_(n→+∞) ∫_0 ^x (t^2^(n+1) /(1−t^2 )) dt =0 because 0≤ ⇒t≤x<1 ⇒ lim_(n→+∞) ∫_0 ^x P_n (t)dt = ∫_0 ^x (dt/(1−t^2 )) =(1/2) ∫_0 ^x ( (1/(1−t)) +(1/(1+t)))dt =[(1/2)ln∣((1+t)/(1−t))∣]_0 ^c =(1/2) ln∣ ((1+x)/(1−x))∣ .](Q33806.png) | ||