Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 33815 by rahul 19 last updated on 25/Apr/18

Let f:D → R be defined as f(x) = ((x^2 +2x+a)/(x^2 +4x+3a)) where D and R denote the domain of f and the set of all real numbers respectively. If f is ′′ surjective ′′ mapping then the range of a is ? a) 0≤a≤1 b) 0<a≤1 c) 0<a<1 d) 0≤a<1

$$\boldsymbol{{L}}{et}\:{f}:{D}\:\rightarrow\:\boldsymbol{{R}}\:{be}\:{defined}\:{as}\: \\ $$$${f}\left({x}\right)\:=\:\frac{{x}^{\mathrm{2}} +\mathrm{2}{x}+{a}}{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{3}{a}}\:{where}\:{D}\:{and}\:{R} \\ $$$${denote}\:{the}\:{domain}\:{of}\:\boldsymbol{{f}}\:{and}\:{the}\:{set} \\ $$$${of}\:{all}\:{real}\:{numbers}\:{respectively}. \\ $$$${If}\:{f}\:{is}\:''\:{surjective}\:''\:\:{mapping}\:{then} \\ $$$${the}\:{range}\:{of}\:\boldsymbol{{a}}\:{is}\:? \\ $$$$\left.{a}\right)\:\mathrm{0}\leqslant{a}\leqslant\mathrm{1} \\ $$$$\left.{b}\right)\:\mathrm{0}<{a}\leqslant\mathrm{1} \\ $$$$\left.{c}\right)\:\mathrm{0}<{a}<\mathrm{1} \\ $$$$\left.{d}\right)\:\mathrm{0}\leqslant{a}<\mathrm{1}\: \\ $$

Answered by MJS last updated on 26/Apr/18

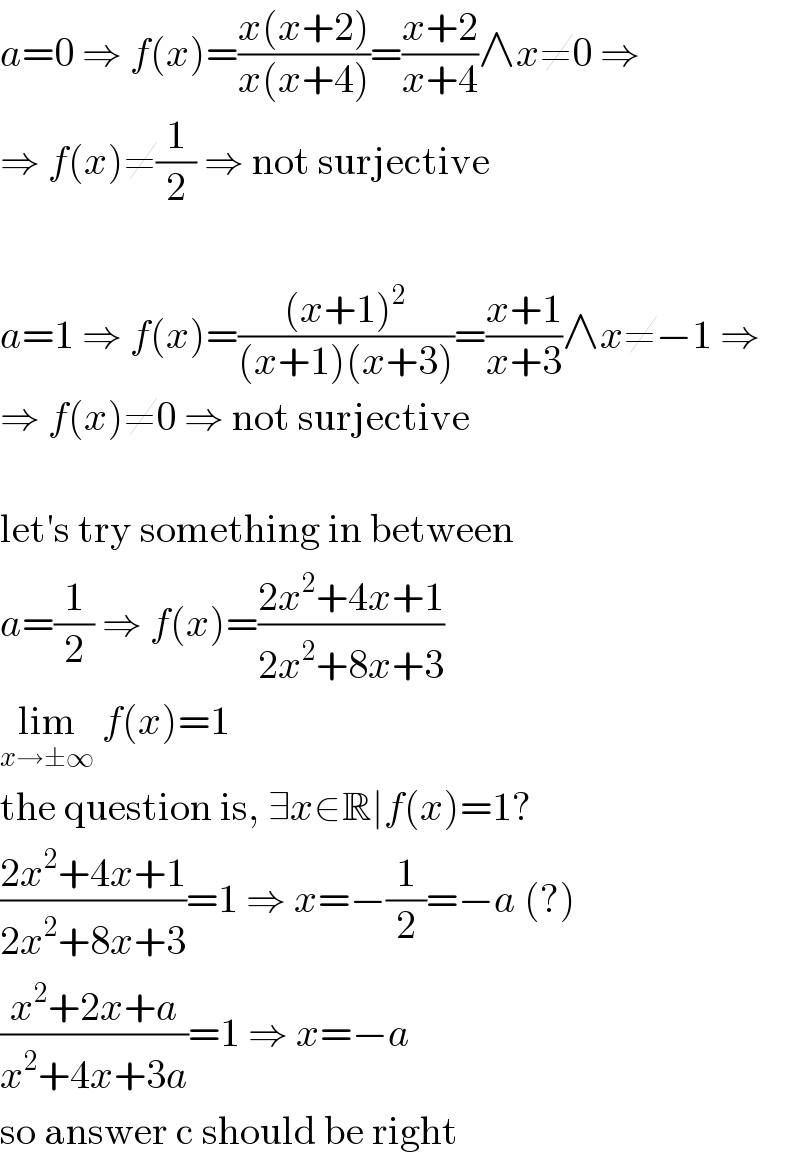
a=0 ⇒ f(x)=((x(x+2))/(x(x+4)))=((x+2)/(x+4))∧x≠0 ⇒ ⇒ f(x)≠(1/2) ⇒ not surjective a=1 ⇒ f(x)=(((x+1)^2 )/((x+1)(x+3)))=((x+1)/(x+3))∧x≠−1 ⇒ ⇒ f(x)≠0 ⇒ not surjective let′s try something in between a=(1/2) ⇒ f(x)=((2x^2 +4x+1)/(2x^2 +8x+3)) lim_(x→±∞) f(x)=1 the question is, ∃x∈R∣f(x)=1? ((2x^2 +4x+1)/(2x^2 +8x+3))=1 ⇒ x=−(1/2)=−a (?) ((x^2 +2x+a)/(x^2 +4x+3a))=1 ⇒ x=−a so answer c should be right

$${a}=\mathrm{0}\:\Rightarrow\:{f}\left({x}\right)=\frac{{x}\left({x}+\mathrm{2}\right)}{{x}\left({x}+\mathrm{4}\right)}=\frac{{x}+\mathrm{2}}{{x}+\mathrm{4}}\wedge{x}\neq\mathrm{0}\:\Rightarrow \\ $$$$\Rightarrow\:{f}\left({x}\right)\neq\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\:\mathrm{not}\:\mathrm{surjective} \\ $$$$ \\ $$$${a}=\mathrm{1}\:\Rightarrow\:{f}\left({x}\right)=\frac{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{\left({x}+\mathrm{1}\right)\left({x}+\mathrm{3}\right)}=\frac{{x}+\mathrm{1}}{{x}+\mathrm{3}}\wedge{x}\neq−\mathrm{1}\:\Rightarrow \\ $$$$\Rightarrow\:{f}\left({x}\right)\neq\mathrm{0}\:\Rightarrow\:\mathrm{not}\:\mathrm{surjective} \\ $$$$ \\ $$$$\mathrm{let}'\mathrm{s}\:\mathrm{try}\:\mathrm{something}\:\mathrm{in}\:\mathrm{between} \\ $$$${a}=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\:{f}\left({x}\right)=\frac{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{8}{x}+\mathrm{3}} \\ $$$$\underset{{x}\rightarrow\pm\infty} {\mathrm{lim}}\:{f}\left({x}\right)=\mathrm{1} \\ $$$$\mathrm{the}\:\mathrm{question}\:\mathrm{is},\:\exists{x}\in\mathbb{R}\mid{f}\left({x}\right)=\mathrm{1}? \\ $$$$\frac{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{8}{x}+\mathrm{3}}=\mathrm{1}\:\Rightarrow\:{x}=−\frac{\mathrm{1}}{\mathrm{2}}=−{a}\:\left(?\right) \\ $$$$\frac{{x}^{\mathrm{2}} +\mathrm{2}{x}+{a}}{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{3}{a}}=\mathrm{1}\:\Rightarrow\:{x}=−{a} \\ $$$$\mathrm{so}\:\mathrm{answer}\:\mathrm{c}\:\mathrm{should}\:\mathrm{be}\:\mathrm{right} \\ $$

Commented by rahul 19 last updated on 28/Apr/18

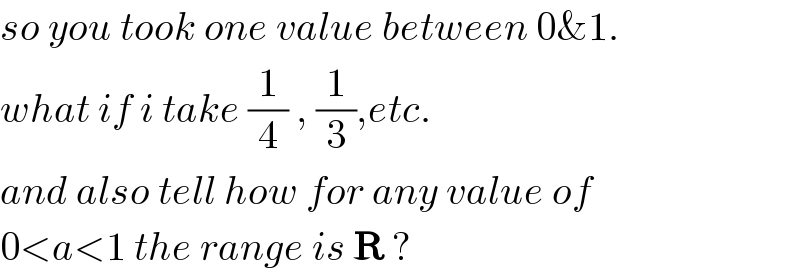
so you took one value between 0&1. what if i take (1/4) , (1/3),etc. and also tell how for any value of 0<a<1 the range is R ?

$${so}\:{you}\:{took}\:{one}\:{value}\:{between}\:\mathrm{0\&1}. \\ $$$${what}\:{if}\:{i}\:{take}\:\frac{\mathrm{1}}{\mathrm{4}}\:,\:\frac{\mathrm{1}}{\mathrm{3}},{etc}.\: \\ $$$${and}\:{also}\:{tell}\:{how}\:{for}\:{any}\:{value}\:{of} \\ $$$$\mathrm{0}<{a}<\mathrm{1}\:{the}\:{range}\:{is}\:\boldsymbol{\mathrm{R}}\:? \\ $$

Commented by MJS last updated on 28/Apr/18

good point ((x^2 +2x+a)/(x^2 +4x+3a))=(((x+1+(√(1−a)))(x+1−(√(1−a))))/((x+2+(√(4−3a)))(x+2−(√(4−3a))))) the same problem as with a=0 ∨ a=1 would occur only if we can shorten this fraction. in this case: x+1+(√(1−a))=x+2+(√(4−3a)) ∨ x+1+(√(1−a))=x+2−(√(4−3a)) ∨ x+1−(√(1−a))=x+2+(√(4−3a)) ∨ x+1−(√(1−a))=x+2+(√(4−3a)) ⇒ a=0 ∨ a=1 ⇒ ∀a∈]0; 1[: ((x^2 +2x+a)/(x^2 +4x+3a))∈R

$$\mathrm{good}\:\mathrm{point} \\ $$$$ \\ $$$$\frac{{x}^{\mathrm{2}} +\mathrm{2}{x}+{a}}{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{3}{a}}=\frac{\left({x}+\mathrm{1}+\sqrt{\mathrm{1}−{a}}\right)\left({x}+\mathrm{1}−\sqrt{\mathrm{1}−{a}}\right)}{\left({x}+\mathrm{2}+\sqrt{\mathrm{4}−\mathrm{3}{a}}\right)\left({x}+\mathrm{2}−\sqrt{\mathrm{4}−\mathrm{3}{a}}\right)} \\ $$$$\mathrm{the}\:\mathrm{same}\:\mathrm{problem}\:\mathrm{as}\:\mathrm{with}\:{a}=\mathrm{0}\:\vee\:{a}=\mathrm{1}\:\mathrm{would} \\ $$$$\mathrm{occur}\:\mathrm{only}\:\mathrm{if}\:\mathrm{we}\:\mathrm{can}\:\mathrm{shorten}\:\mathrm{this}\:\mathrm{fraction}. \\ $$$$\mathrm{in}\:\mathrm{this}\:\mathrm{case}: \\ $$$${x}+\mathrm{1}+\sqrt{\mathrm{1}−{a}}={x}+\mathrm{2}+\sqrt{\mathrm{4}−\mathrm{3}{a}}\:\vee \\ $$$${x}+\mathrm{1}+\sqrt{\mathrm{1}−{a}}={x}+\mathrm{2}−\sqrt{\mathrm{4}−\mathrm{3}{a}}\:\vee \\ $$$${x}+\mathrm{1}−\sqrt{\mathrm{1}−{a}}={x}+\mathrm{2}+\sqrt{\mathrm{4}−\mathrm{3}{a}}\:\vee \\ $$$${x}+\mathrm{1}−\sqrt{\mathrm{1}−{a}}={x}+\mathrm{2}+\sqrt{\mathrm{4}−\mathrm{3}{a}} \\ $$$$\Rightarrow\:{a}=\mathrm{0}\:\vee\:{a}=\mathrm{1} \\ $$$$\left.\Rightarrow\:\forall{a}\in\right]\mathrm{0};\:\mathrm{1}\left[:\:\frac{{x}^{\mathrm{2}} +\mathrm{2}{x}+{a}}{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{3}{a}}\in\mathbb{R}\right. \\ $$

Commented by rahul 19 last updated on 29/Apr/18

Thank you sir.

$$\mathscr{T}\mathrm{hank}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com