Let f:R → [ 1, ∞) be defined as f(x) = log_(10) ((√(3x^2 −4x+k+1)) +10 ). If f(x) is surjective , then find the value of k ?


Question and Answers Forum

All Questions Topic List
Relation and Functions Questions
Previous in All Question Next in All Question
Previous in Relation and Functions Next in Relation and Functions
Question Number 33818 by rahul 19 last updated on 25/Apr/18

$L e t f : R \to [1, \infty) b e d e f i n e d a s$ $f (x) = \log_{10} (\sqrt{3 x^{2} - 4 x + k + 1} + 10) .$ $I f f (x) i s s u r j e c t i v e, t h e n f i n d$ $t h e v a l u e o f k ?$
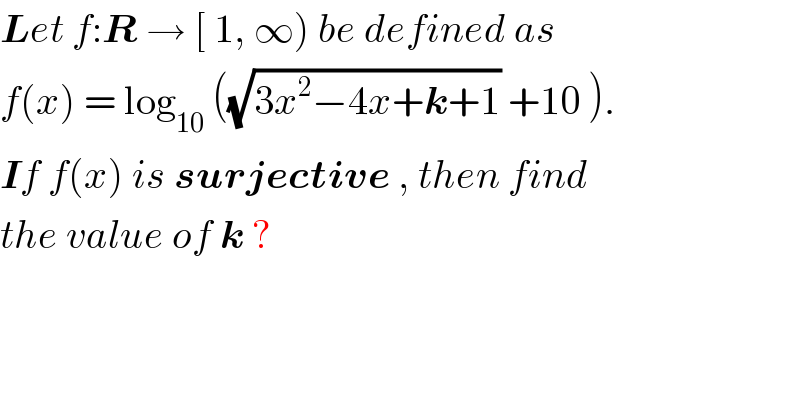
	Answered by MJS last updated on 26/Apr/18

	$this {one}^{'} s easier$ $\sqrt{3 x^{2} - 4 x + k + 1} must be a real number$ $and must have exactly one zero$ $(2 distinct zeros \Rightarrow f (x) not defined for$ $some x \in R; no zeros \Rightarrow m i n (f (x)) > 1)$ $3 x^{2} - 4 x + k + 1 = 0$ $x^{2} - \frac{4}{3} x + \frac{k + 1}{3} = 0$ $x = \frac{2}{3} \pm \frac{\sqrt{1 - 3 k}}{3}$ $1 - 3 k = 0 \Rightarrow k = \frac{1}{3}$
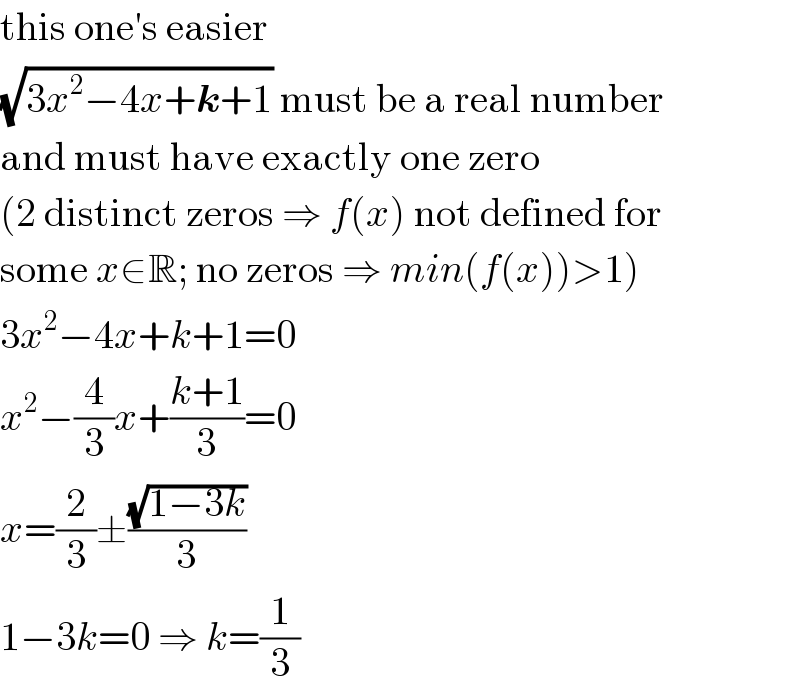
	Commented by rahul 19 last updated on 28/Apr/18

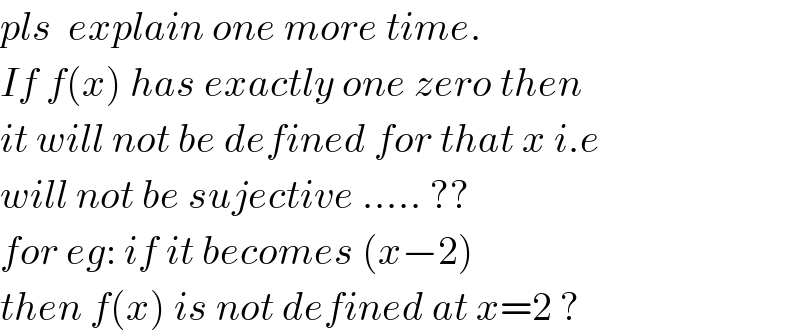
	$p l s e x p l a i n o n e m o r e t i m e .$ $I f f (x) h a s e x a c t l y o n e z e r o t h e n$ $i t w i l l n o t b e d e f i n e d f o r t h a t x i . e$ $w i l l n o t b e s u j e c t i v e . . . . . ? ?$ $f o r e g : i f i t b e c o m e s (x - 2)$ $t h e n f (x) i s n o t d e f i n e d a t x = 2 ?$
	Commented by MJS last updated on 28/Apr/18
	$not f(x), I only talk about the root f(x)=log_(10) ((√(g(x)))+10) g(x) has { ((no zero ⇒ (√(g(x)))>0 ∧ f(x)>1 ∀x∈R ⇒)),((⇒ ∃y∈[1; ∞[: y≠f(x)∀x∈R)),((1 zero p ⇒ (√(g(p)))=0 ⇒ f(p)=1 ⇒)),((⇒ ∀y∈[1; ∞[: ∃x∈R: y=f(x) ⇒ f(x) is surjective)),((2 zeros p, q ⇒ (√(g(x)))∉R ∀x∈]p; q[ ⇒)),((⇒ D=R\x≠R ∀x∈]p; q[)) :}$
	$not f (x), I only talk about the root$ $f (x) = \log_{10} (\sqrt{g (x)} + 10)$ $g (x) has {\begin{cases} no zero \Rightarrow \sqrt{g (x)} > 0 \land f (x) > 1 \forall x \in R \Rightarrow \\ \Rightarrow \exists y \in [1; \infty [: y \neq f (x) \forall x \in R \\ 1 zero p \Rightarrow \sqrt{g (p)} = 0 \Rightarrow f (p) = 1 \Rightarrow \\ \Rightarrow \forall y \in [1; \infty [: \exists x \in R : y = f (x) \Rightarrow f (x) is surjective \\ 2 zeros p, q \Rightarrow \sqrt{g (x)} \notin R \forall x \in] p; q [\Rightarrow \\ \Rightarrow D = R ∖ x \neq R \forall x \in] p; q [ \end{cases}$
	Commented by rahul 19 last updated on 29/Apr/18

	$T h a n k y o u s i r .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum