
Question and Answers Forum
Question Number 33845 by prof Abdo imad last updated on 26/Apr/18
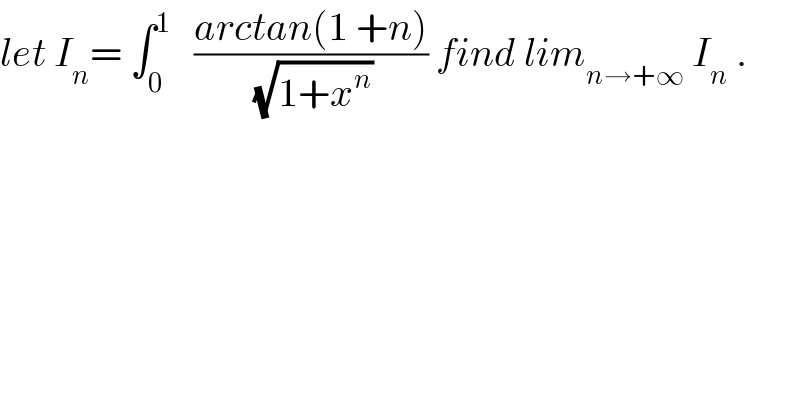
Commented by prof Abdo imad last updated on 27/Apr/18
![I_n = ∫_R ((arctan(1+n))/(√(1+x^n ))) χ_([0,1]) (x)dx but f_n (x)= ((arctan(1+n))/(√(1+x^n ))) χ_([0,1]) (x)_(n→+∞) →f(x)=(π/2) on[0,1] so ∫_R f_n (x)dx → ∫_0 ^1 f(x)dx =(π/2) .](Q33917.png)
| ||
Question and Answers Forum | ||
Question Number 33845 by prof Abdo imad last updated on 26/Apr/18 | ||
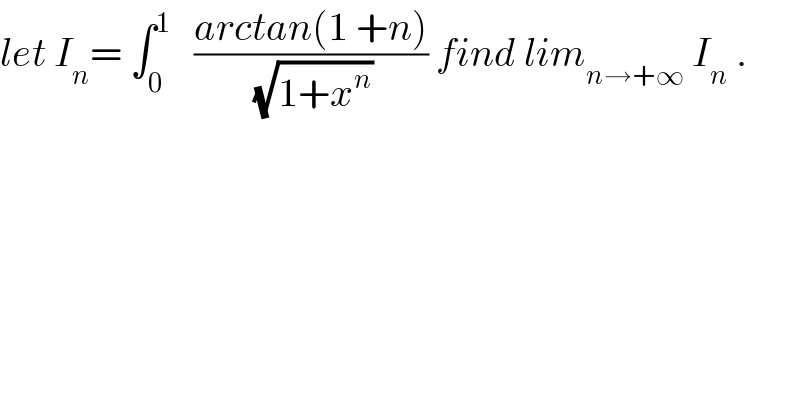 | ||
Commented by prof Abdo imad last updated on 27/Apr/18 | ||
![I_n = ∫_R ((arctan(1+n))/(√(1+x^n ))) χ_([0,1]) (x)dx but f_n (x)= ((arctan(1+n))/(√(1+x^n ))) χ_([0,1]) (x)_(n→+∞) →f(x)=(π/2) on[0,1] so ∫_R f_n (x)dx → ∫_0 ^1 f(x)dx =(π/2) .](Q33917.png) | ||