
Previous in Relation and Functions Next in Relation and Functions
Question Number 33847 by prof Abdo imad last updated on 26/Apr/18
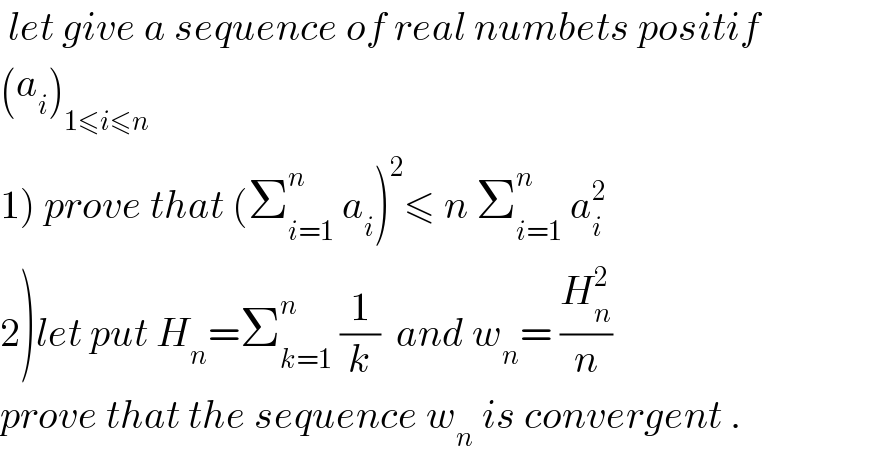
$$\:{let}\:{give}\:{a}\:{sequence}\:{of}\:{real}\:{numbets}\:{positif} \\ $$$$\left({a}_{{i}} \right)_{\mathrm{1}\leqslant{i}\leqslant{n}} \\ $$$$\left.\mathrm{1}\right)\:{prove}\:{that}\:\left(\sum_{{i}=\mathrm{1}} ^{{n}} \:{a}_{{i}} \right)^{\mathrm{2}} \leqslant\:{n}\:\sum_{{i}=\mathrm{1}} ^{{n}} \:{a}_{{i}} ^{\mathrm{2}} \\ $$$$\left.\mathrm{2}\right){let}\:{put}\:{H}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}}\:\:{and}\:{w}_{{n}} =\:\frac{{H}_{{n}} ^{\mathrm{2}} }{{n}} \\ $$$${prove}\:{that}\:{the}\:{sequence}\:{w}_{{n}} \:{is}\:{convergent}\:. \\ $$
Commented by prof Abdo imad last updated on 27/Apr/18
![for all sequences of reals numbers positifs (a_i )_(1≤i≤n) and (b_i )_(1≤i≤n) we have Σ_(i=1) ^n a_i b_i ≤ (Σ_(i=1) ^n a_i ^2 )^(1/2) (Σ_(i=1) ^n b_i ^2 )^(1/2) (holder inequality) let take b_i =1 ∀i∈[[1,n]] ⇒Σ_(i=1) ^n a_i ≤(√n) (Σ_(i=1) ^n a_i ^2 )^(1/2) ⇒ (Σ_(i=1) ^n a_i )^2 ≤n(Σ_(i=1) ^n a_i ^2 ) 2)let take a_i = (1/i) ∀i∈[1,n] ⇒(Σ_(i=1) ^n (1/i))^2 ≤nΣ_(i=1) ^n (1/i^2 ) ⇒ H_n ^2 ≤ n Σ_(i=1) ^n (1/i^2 ) ⇒ (H_n ^2 /n) ≤ Σ_(i=1) ^n (1/i^2 ) ⇒ w_n ≤ Σ_(i=1) ^n (1/i^2 ) Rieman serie convergent so (w_n ) is convergent.](Q33920.png)
$${for}\:{all}\:{sequences}\:{of}\:{reals}\:{numbers}\:{positifs} \\ $$$$\left({a}_{{i}} \right)_{\mathrm{1}\leqslant{i}\leqslant{n}} {and}\:\left({b}_{{i}} \right)_{\mathrm{1}\leqslant{i}\leqslant{n}} \:{we}\:{have} \\ $$$$\sum_{{i}=\mathrm{1}} ^{{n}} \:{a}_{{i}} {b}_{{i}} \:\leqslant\:\left(\sum_{{i}=\mathrm{1}} ^{{n}} {a}_{{i}} ^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} \left(\sum_{{i}=\mathrm{1}} ^{{n}} {b}_{{i}} ^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} \:\left({holder}\:{inequality}\right) \\ $$$${let}\:{take}\:{b}_{{i}} =\mathrm{1}\:\forall{i}\in\left[\left[\mathrm{1},{n}\right]\right]\:\Rightarrow\sum_{{i}=\mathrm{1}} ^{{n}} {a}_{{i}} \:\leqslant\sqrt{{n}}\:\left(\sum_{{i}=\mathrm{1}} ^{{n}} {a}_{{i}} ^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} \Rightarrow \\ $$$$\left(\sum_{{i}=\mathrm{1}} ^{{n}} {a}_{{i}} \right)^{\mathrm{2}} \:\leqslant{n}\left(\sum_{{i}=\mathrm{1}} ^{{n}} {a}_{{i}} ^{\mathrm{2}} \right) \\ $$$$\left.\mathrm{2}\right){let}\:{take}\:\:{a}_{{i}} =\:\frac{\mathrm{1}}{{i}}\:\:\forall{i}\in\left[\mathrm{1},{n}\right]\:\Rightarrow\left(\sum_{{i}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{i}}\right)^{\mathrm{2}} \leqslant{n}\sum_{{i}=\mathrm{1}} ^{{n}} \frac{\mathrm{1}}{{i}^{\mathrm{2}} } \\ $$$$\Rightarrow\:{H}_{{n}} ^{\mathrm{2}} \:\leqslant\:{n}\:\sum_{{i}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{i}^{\mathrm{2}} }\:\Rightarrow\:\frac{{H}_{{n}} ^{\mathrm{2}} }{{n}}\:\leqslant\:\sum_{{i}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{i}^{\mathrm{2}} }\:\Rightarrow \\ $$$${w}_{{n}} \:\leqslant\:\sum_{{i}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{i}^{\mathrm{2}} }\:\:{Rieman}\:{serie}\:{convergent}\:{so} \\ $$$$\left({w}_{{n}} \right)\:{is}\:{convergent}. \\ $$
