
Question and Answers Forum
Question Number 33894 by math khazana by abdo last updated on 26/Apr/18
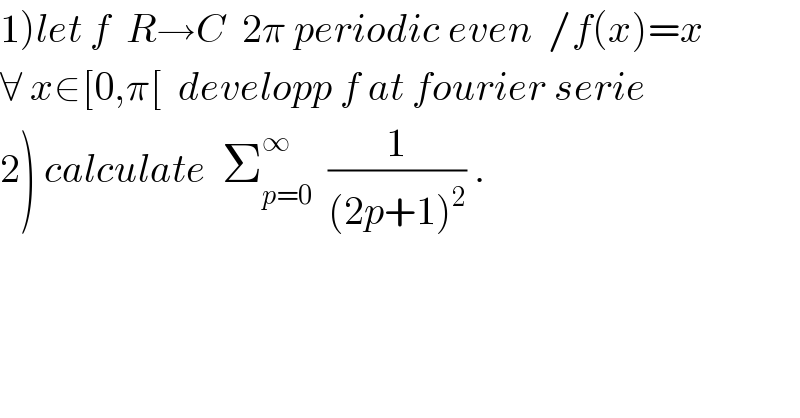
Commented by abdo imad last updated on 28/Apr/18
![f is even so f(x)=(a_0 /2) +Σ_(n=1) ^∞ a_n cos(nx)with a_n = (2/T) ∫_([T]) f(x)cos(nx)dx=(2/(2π)) ∫_(−π) ^π x cos(nx)dx =(2/π) ∫_0 ^π xcos(nx)dx⇒ (π/2)a_n =∫_0 ^π xcos(nx)dx let integrate by parts u^ =x and v^′ =cos(nx)⇒ (π/2)a_n =((x/n)sin(nx)]_0 ^π −∫_0 ^π (1/n)sin(nx)dx =−(1/n)∫_0 ^π sin(nx)=(1/n^2 )[cos(nx)]_0 ^π =(1/n^2 )((−1)^n −1) ⇒ a_n =(2/(πn^2 ))((−1)^n −1)⇒a_(2n) =0 and a_(2n+1) =((−4)/(π(2n+1)^2 )) (π/2)a_0 =∫_0 ^π xdx=(π^2 /2) ⇒a_0 =π ⇒ f(x) = (π/2) −(4/π) Σ_(n=0) ^∞ ((cos(2n+1)x)/((2n+1)^2 )) (d) 2) let take x=0 in (d) we get 0=(π/2) −(4/π) Σ_(n=0) ^∞ (1/((2n+1)^2 )) ⇒(4/π) Σ_(n=0) ^∞ (1/((2n+1)^2 )) =(π/2) ⇒ Σ_(n=0) ^∞ (1/((2n+1)^2 )) =(π^2 /8) .](Q33973.png)
| ||
Question and Answers Forum | ||
Question Number 33894 by math khazana by abdo last updated on 26/Apr/18 | ||
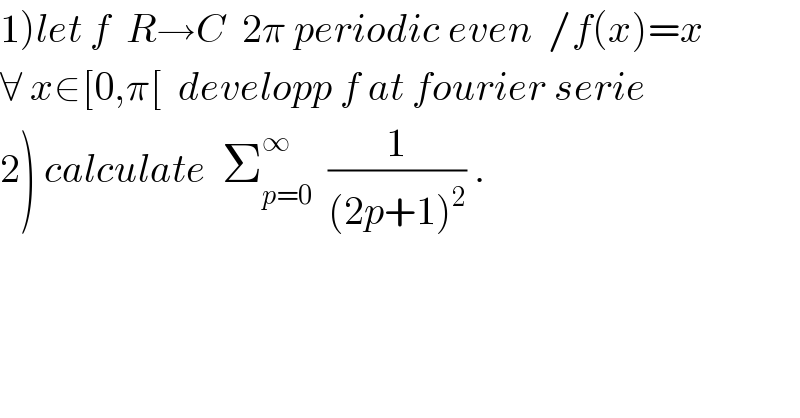 | ||
Commented by abdo imad last updated on 28/Apr/18 | ||
![f is even so f(x)=(a_0 /2) +Σ_(n=1) ^∞ a_n cos(nx)with a_n = (2/T) ∫_([T]) f(x)cos(nx)dx=(2/(2π)) ∫_(−π) ^π x cos(nx)dx =(2/π) ∫_0 ^π xcos(nx)dx⇒ (π/2)a_n =∫_0 ^π xcos(nx)dx let integrate by parts u^ =x and v^′ =cos(nx)⇒ (π/2)a_n =((x/n)sin(nx)]_0 ^π −∫_0 ^π (1/n)sin(nx)dx =−(1/n)∫_0 ^π sin(nx)=(1/n^2 )[cos(nx)]_0 ^π =(1/n^2 )((−1)^n −1) ⇒ a_n =(2/(πn^2 ))((−1)^n −1)⇒a_(2n) =0 and a_(2n+1) =((−4)/(π(2n+1)^2 )) (π/2)a_0 =∫_0 ^π xdx=(π^2 /2) ⇒a_0 =π ⇒ f(x) = (π/2) −(4/π) Σ_(n=0) ^∞ ((cos(2n+1)x)/((2n+1)^2 )) (d) 2) let take x=0 in (d) we get 0=(π/2) −(4/π) Σ_(n=0) ^∞ (1/((2n+1)^2 )) ⇒(4/π) Σ_(n=0) ^∞ (1/((2n+1)^2 )) =(π/2) ⇒ Σ_(n=0) ^∞ (1/((2n+1)^2 )) =(π^2 /8) .](Q33973.png) | ||