Let a,b are positive real numbers such that a−b=10 , then the smallest value of the constant k for which (√((x^2 +ax))) − (√((x^2 +bx)))


Question and Answers Forum

All Questions Topic List
Relation and Functions Questions
Previous in All Question Next in All Question
Previous in Relation and Functions Next in Relation and Functions
Question Number 33940 by rahul 19 last updated on 28/Apr/18

$L e t a, b a r e p o s i t i v e r e a l n u m b e r s s u c h$ $t h a t a - b = 10, t h e n t h e s m a l l e s t v a l u e$ $o f t h e c o n s t a n t k f o r w h i c h$ $\sqrt{(x^{2} + a x)} - \sqrt{(x^{2} + b x)} < k f o r a l l x > 0$ $i s ?$
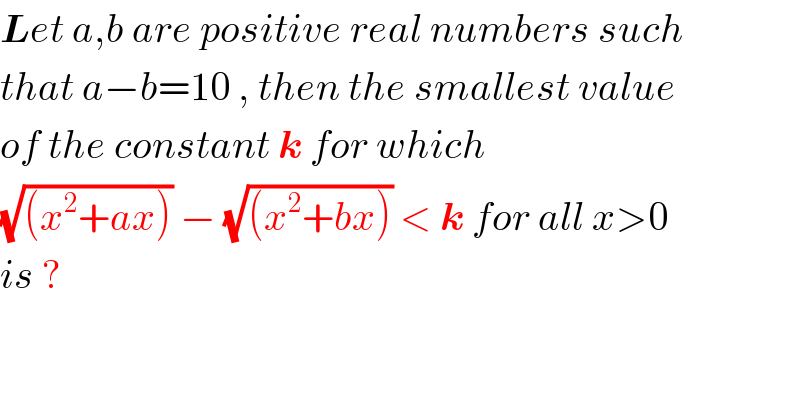
	Answered by MJS last updated on 28/Apr/18

	$a = r + 5$ $b = r - 5$ $\sqrt{x^{2} + r x + 5 x} - \sqrt{x^{2} + r x - 5 x} < k$ $we have to show that$ $\lim_{x \to \infty} \sqrt{x^{2} + r x + 5 x} - \sqrt{x^{2} + r x - 5 x} = 5$ $sorry I have no time right now . . .$ $\sqrt{x^{2} + r x + 5 x} - \sqrt{x^{2} + r x - 5 x} = k (I .)$ $[x = y \Rightarrow \frac{1}{x} = \frac{1}{y}]$ $\frac{1}{\sqrt{x^{2} + r x + 5 x} - \sqrt{x^{2} + r x - 5 x}} = \frac{1}{k}$ $[\frac{1}{u - v} = \frac{u + v}{(u - v) (u + v)} = \frac{u + v}{u^{2} - v^{2}}]$ $\frac{\sqrt{x^{2} + r x + 5 x} + \sqrt{x^{2} + r x - 5 x}}{x^{2} + r x + 5 x - (x^{2} + r x - 5 x)} = \frac{1}{k}$ $\frac{\sqrt{x^{2} + r x + 5 x} + \sqrt{x^{2} + r x - 5 x}}{10 x} = \frac{1}{k}$ $\sqrt{x^{2} + r x + 5 x} + \sqrt{x^{2} + r x - 5 x} = \frac{10 x}{k} (I I .)$ $2 \sqrt{x^{2} + r x + 5 x} = k + \frac{10 x}{k} (I . + I I .)$ $4 (x^{2} + r x + 5 x) = k^{2} + 20 x + \frac{100 x^{2}}{k^{2}}$ $(4 - \frac{100}{k^{2}}) x^{2} + 4 r x - k^{2} = 0$ $x^{2} + \frac{k^{2} r}{k^{2} - 25} x - \frac{k^{4}}{4 (k^{2} - 25)} = 0$ $x = - \frac{k^{2} r}{2 (k^{2} - 25)} \pm \frac{k^{2}}{2 (k^{2} - 25)} \sqrt{k^{2} + r^{2} - 25} =$ $= \frac{r \pm \sqrt{k^{2} + r^{2} - 25}}{2 (k^{2} - 25)} k^{2}$ $\frac{1}{x} = \frac{2 (k^{2} - 25)}{r \pm \sqrt{k^{2} + r^{2} - 25}} \times \frac{1}{k^{2}}$ $x \to \infty \Rightarrow k^{2} - 25 = 0 \Rightarrow k = \pm 5$ $\sqrt{x^{2} + r x + 5 x} - \sqrt{x^{2} + r x - 5 x} > 0 \Rightarrow k = 5$
	Commented byrahul 19 last updated on 28/Apr/18

	$N o problem sir .$ $btw, h o w y o u c a m e t o k n o w i t s h o u l d$ $b e e q u a l t o 5 ?$
	Commented byMJS last updated on 28/Apr/18

	$this is what seems obvious to me :$ $\sqrt{x (x + c)} = \sqrt{{(x + \frac{c}{2})}^{2} - \frac{c^{2}}{4}} \underset{x \to \infty}{\approx} x + \frac{c}{2}$ $\sqrt{x (x + a)} - \sqrt{x (x + b)} \underset{x \to \infty}{\approx} x + \frac{a}{2} - (x + \frac{b}{2}) = \frac{a - b}{2} = \frac{a - (a - 10)}{2} = 5$ $not sure if this counts as proof . . .$
	Commented byrahul 19 last updated on 28/Apr/18

	$T h a n k you sir .$
	Answered by tanmay.chaudhury50@gmail.com last updated on 28/Apr/18

	$\sqrt{(x^{2} + a x)} - \sqrt{(x^{2} + b x)} < k$ $x (a - b) / \sqrt{(x_{}^{2} + a x)} + \sqrt{(x^{2} + b x)} < k$ $(a - b) / \sqrt{(1 + a / x)} + \sqrt{(1 + b / x)} < k$ $10 / \sqrt{(1 + a / x)} + \sqrt{(1 + b / x)} < k$ $f o r s m a l l e s t v a l u e o f k t h e d e n o m i n a t o r s h o u l b e$ $b e m a x i m u m v a l u e$ $m a x i m u m v a l u e \sqrt{(1 + a / x)} + \sqrt{(1 + b / x)}$ $p l s c h e c k t h e q u e s t i o n$
	Commented byrahul 19 last updated on 28/Apr/18

	$W o w! n i c e s o l u t i o n s i r!$
	Answered by tanmay.chaudhury50@gmail.com last updated on 28/Apr/18

	$f x \to \infty t h e v a l u e o f \sqrt{(1 + a / x)} + \sqrt{(1 + b / x)}$ $i s 2 s o t h e v a l u e o f k i s 10 / 2 = 5$
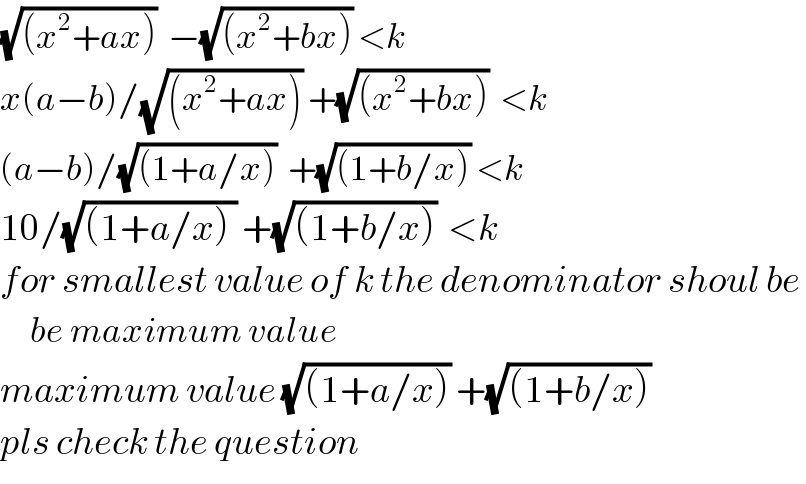
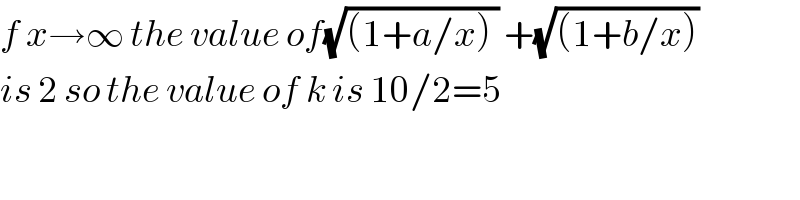
	Commented byrahul 19 last updated on 29/Apr/18

	$d o u b t :$ $w e n e e d t o f i n d m a x . v a l u e o f$ $\sqrt{1 + \frac{a}{x}} + \sqrt{1 + \frac{b}{x}} \to m i n . v a l u e o f x$ $s o w h y x \to \infty ? ? ? i t s h o u l d b e x \to 0!$
	Commented bytanmay.chaudhury50@gmail.com last updated on 29/Apr/18

	$c h e c k t h e q u e s t i o n . . . . w h e n x \to \infty t h e e x p r e s s i o n$ $h a s m i n v a l u e t h a t i s 2$ $t h e v a l u e o f k i s 10 / 2 = 5$ $w h e n x \to 0 t h e e x p r e s s i o n b e c o m e \infty, t h e n$ $v a l u e o f k i s 10 / \infty = 0$ $m i n v a l u e o f k = 0 a n d m a x v a l u e o f k = 5$ $t h e q u e s t i o n p o s t e d b y y o u h a s s o m e e r r o r$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum