Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 33978 by abdo imad last updated on 28/Apr/18

$$letf\left(t\right)={\int }_0^{\mathrm{\infty }}\frac{sin\left(x^2\right)e^{-{tx}^2}}{x^2}dxwitht>0$$ $$findasimpleformof{f}^{{}^{\prime }}\left(t\right).$$

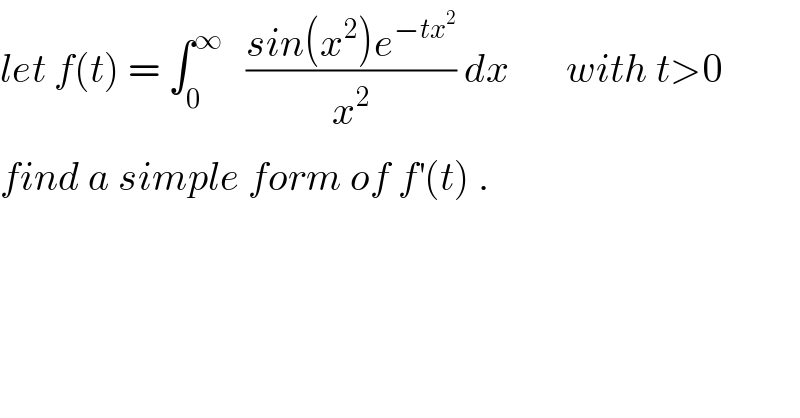
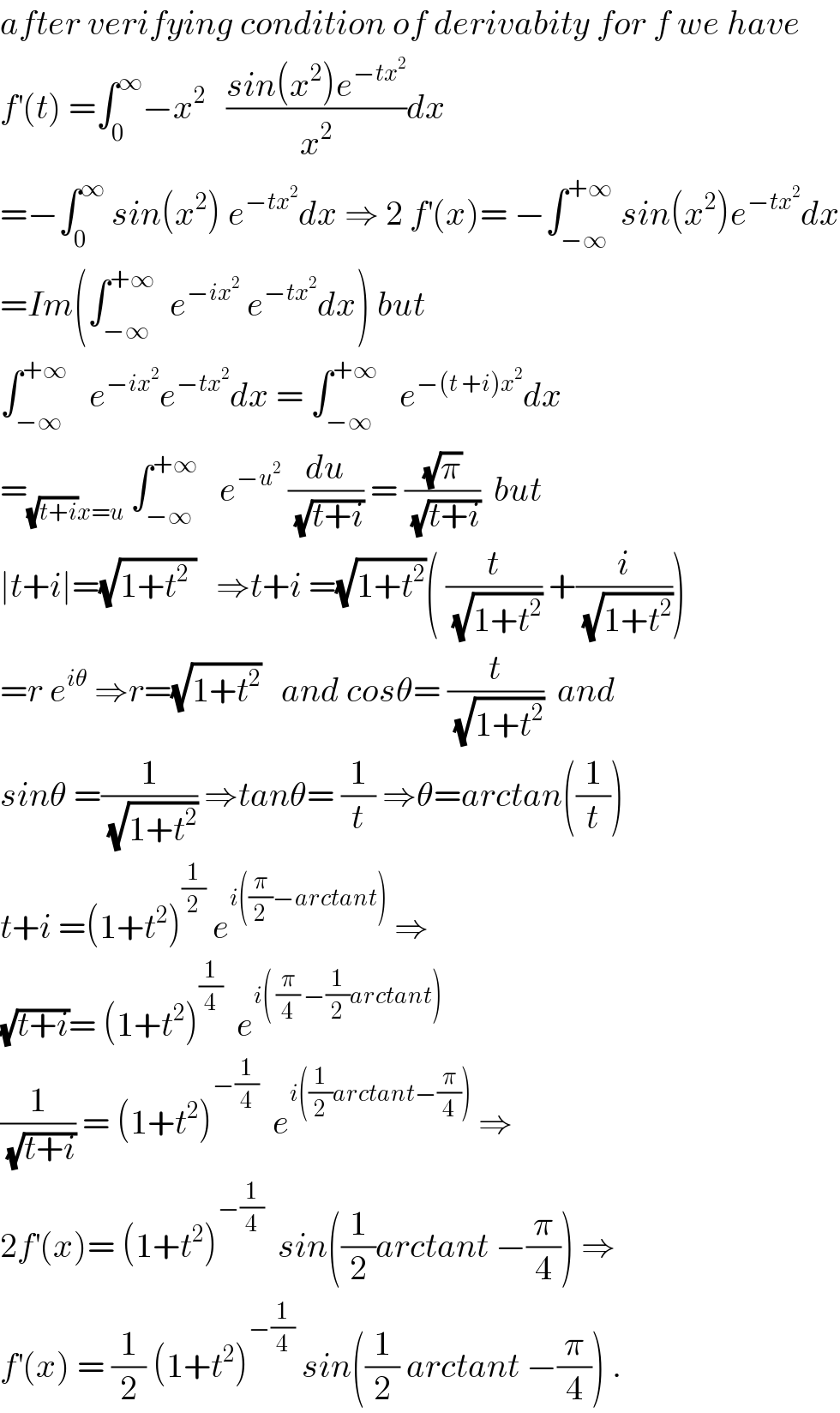
Commented bymath khazana by abdo last updated on 01/May/18

$$afterverifyingconditionofderivabityforfwehave$$ $$f^{{}^{\prime }}\left(t\right)={\int }_0^{\mathrm{\infty }}-x^2\frac{sin\left(x^2\right)e^{-{tx}^2}}{x^2}dx$$ $$=-{\int }_0^{\mathrm{\infty }}sin\left(x^2\right)e^{-{tx}^2}dx\Rightarrow 2f^{{}^{\prime }}\left(x\right)=-{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}sin\left(x^2\right)e^{-{tx}^2}dx$$ $$=Im\left({\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}{e}^{-{ix}^2}{e}^{-{tx}^2}dx\right)but$$ $${\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}{e}^{-{ix}^2}{e}^{-{tx}^2}dx={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}{e}^{-(t+i)x^2}dx$$ $${=}_{\sqrt{t+i}x=u}{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}{e}^{-u^2}\frac{du}{\sqrt{t+i}}=\frac{\sqrt{\pi }}{\sqrt{t+i}}but$$ $$\mid t+i\mid =\sqrt{1+t^2}\Rightarrow t+i=\sqrt{1+t^2}(\frac{t}{\sqrt{1+t^2}}+\frac{i}{\sqrt{1+t^2}})$$ $$=r{e}^{i\theta }\Rightarrow r=\sqrt{1+t^2}andcos\theta =\frac{t}{\sqrt{1+t^2}}and$$ $$sin\theta =\frac{1}{\sqrt{1+t^2}}\Rightarrow tan\theta =\frac{1}{t}\Rightarrow \theta =arctan\left(\frac{1}{t}\right)$$ $$t+i={(1+t^2)}^{\frac{1}{2}}{e}^{i(\frac{\pi }{2}-arctant)}\Rightarrow$$ $$\sqrt{t+i}={(1+t^2)}^{\frac{1}{4}}{e}^{i(\frac{\pi }{4}-\frac{1}{2}arctant)}$$ $$\frac{1}{\sqrt{t+i}}={(1+t^2)}^{-\frac{1}{4}}{e}^{i(\frac{1}{2}arctant-\frac{\pi }{4})}\Rightarrow$$ $$2f^{{}^{\prime }}\left(x\right)={(1+t^2)}^{-\frac{1}{4}}sin(\frac{1}{2}arctant-\frac{\pi }{4})\Rightarrow$$ $$f^{{}^{\prime }}\left(x\right)=\frac{1}{2}{(1+t^2)}^{-\frac{1}{4}}sin(\frac{1}{2}arctant-\frac{\pi }{4}).$$

Commented bymath khazana by abdo last updated on 01/May/18

$$f^{{}^{\prime }}\left(t\right)=\frac{1}{2}{(1+t^2)}^{-\frac{1}{4}}sin(\frac{1}{2}arctant-\frac{\pi }{4}).$$

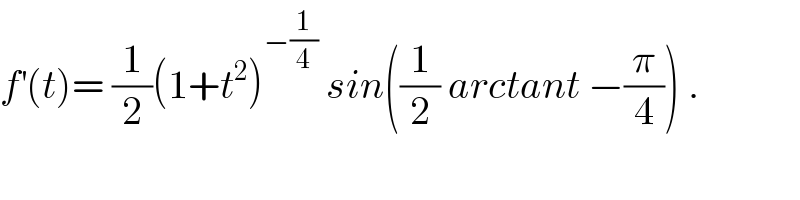
Answered by candre last updated on 30/Apr/18

$$f\left(t\right)=\underset{0}{\stackrel{\mathrm{\infty }}{\int }}\frac{\sin x^2{e}^{-{tx}^2}}{x^2}dx$$ $$letsusethefactthat$$ $$\underset{-\mathrm{\infty }}{\stackrel{+\mathrm{\infty }}{\int }}{e}^{-{ax}^2}dx=\sqrt{\frac{\pi }{a}}$$ $$\sin x=\frac{e^{ix}-e^{-ix}}{2i}$$ $$weget$$ $$\frac{df}{dt}=\underset{0}{\stackrel{\mathrm{\infty }}{\int }}\frac{\partial }{\partial t}\frac{\sin x^2{e}^{-{tx}^2}}{x^2}dx$$ $$=-\underset{0}{\stackrel{\mathrm{\infty }}{\int }}\sin x^2{e}^{-{tx}^2}dx$$ $$=-\underset{0}{\stackrel{\mathrm{\infty }}{\int }}\frac{e^{{ix}^2}-e^{-{ix}^2}}{2i}{e}^{-{tx}^2}dx$$ $$=-\frac{1}{2i}[\underset{0}{\stackrel{\mathrm{\infty }}{\int }}{e}^{(i-t)x^2}dx-\underset{0}{\stackrel{\mathrm{\infty }}{\int }}{e}^{-(i+t)x^2}dx]$$ $$=\frac{\sqrt{\pi }}{4i}(\sqrt{\frac{1}{t+i}}-\sqrt{\frac{1}{t-i}})$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com