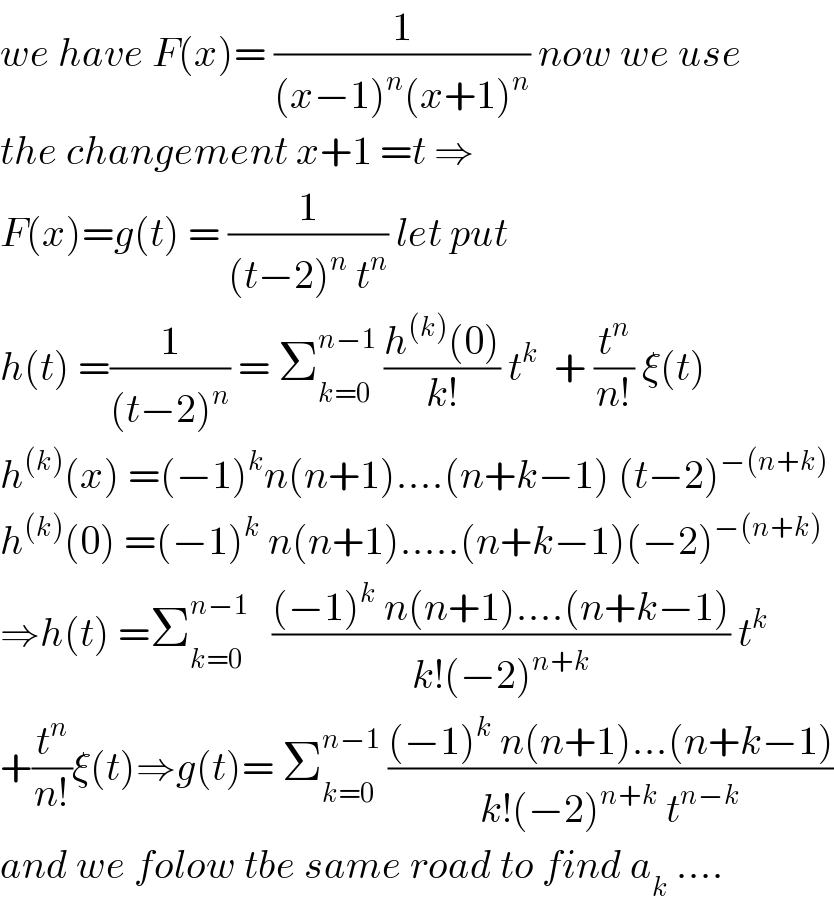Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 34019 by prof Abdo imad last updated on 29/Apr/18

n integr decompose imsidr R[x] the fraction F(x) = (1/((x^2 −1)^n ))

$${n}\:{integr}\:{decompose}\:{imsidr}\:{R}\left[{x}\right]\:{the}\:{fraction} \\ $$$${F}\left({x}\right)\:=\:\:\:\frac{\mathrm{1}}{\left({x}^{\mathrm{2}} \:−\mathrm{1}\right)^{{n}} } \\ $$

Commented by abdo mathsup 649 cc last updated on 06/May/18

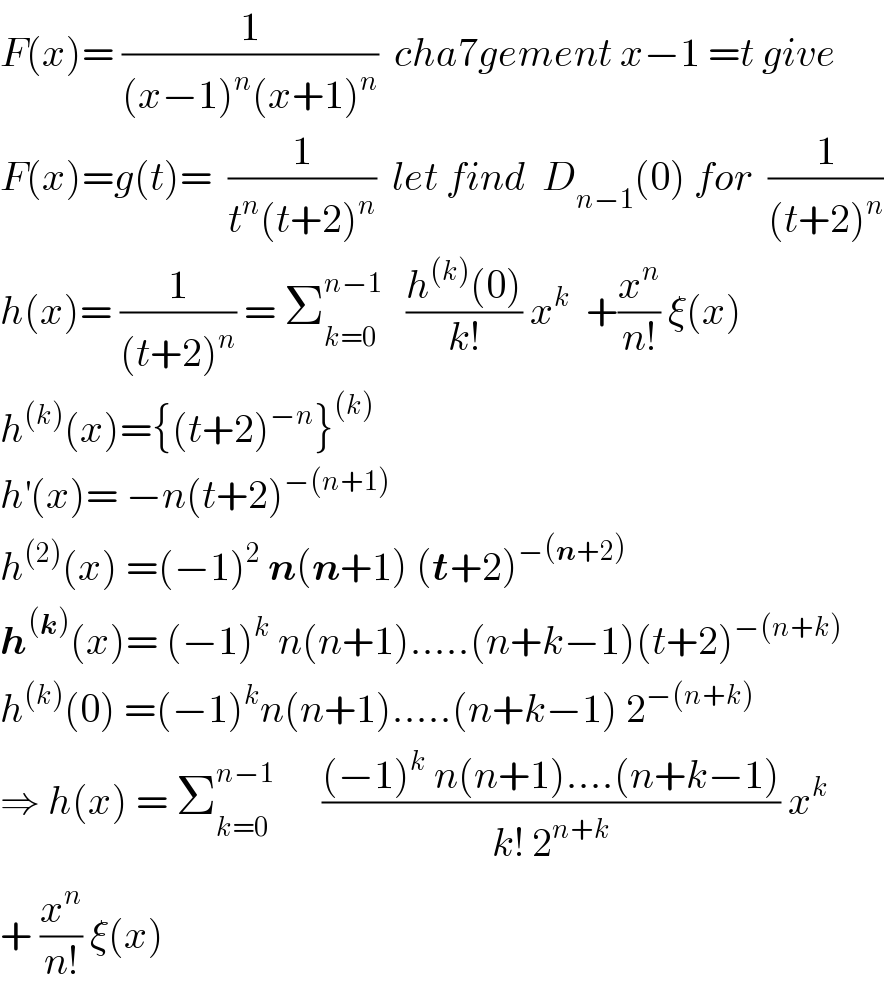
F(x)= (1/((x−1)^n (x+1)^n )) cha7gement x−1 =t give F(x)=g(t)= (1/(t^n (t+2)^n )) let find D_(n−1) (0) for (1/((t+2)^n )) h(x)= (1/((t+2)^n )) = Σ_(k=0) ^(n−1) ((h^((k)) (0))/(k!)) x^k +(x^n /(n!)) ξ(x) h^((k)) (x)={(t+2)^(−n) }^((k)) h^′ (x)= −n(t+2)^(−(n+1)) h^((2)) (x) =(−1)^2 n(n+1) (t+2)^(−(n+2)) h^((k)) (x)= (−1)^k n(n+1).....(n+k−1)(t+2)^(−(n+k)) h^((k)) (0) =(−1)^k n(n+1).....(n+k−1) 2^(−(n+k)) ⇒ h(x) = Σ_(k=0) ^(n−1) (((−1)^k n(n+1)....(n+k−1))/(k! 2^(n+k) )) x^k + (x^n /(n!)) ξ(x)

$${F}\left({x}\right)=\:\frac{\mathrm{1}}{\left({x}−\mathrm{1}\right)^{{n}} \left({x}+\mathrm{1}\right)^{{n}} }\:\:{cha}\mathrm{7}{gement}\:{x}−\mathrm{1}\:={t}\:{give} \\ $$$${F}\left({x}\right)={g}\left({t}\right)=\:\:\frac{\mathrm{1}}{{t}^{{n}} \left({t}+\mathrm{2}\right)^{{n}} }\:\:{let}\:{find}\:\:{D}_{{n}−\mathrm{1}} \left(\mathrm{0}\right)\:{for}\:\:\frac{\mathrm{1}}{\left({t}+\mathrm{2}\right)^{{n}} } \\ $$$${h}\left({x}\right)=\:\frac{\mathrm{1}}{\left({t}+\mathrm{2}\right)^{{n}} }\:=\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:\:\frac{{h}^{\left({k}\right)} \left(\mathrm{0}\right)}{{k}!}\:{x}^{{k}} \:\:+\frac{{x}^{{n}} }{{n}!}\:\xi\left({x}\right) \\ $$$${h}^{\left({k}\right)} \left({x}\right)=\left\{\left({t}+\mathrm{2}\right)^{−{n}} \right\}^{\left({k}\right)} \\ $$$${h}^{'} \left({x}\right)=\:−{n}\left({t}+\mathrm{2}\right)^{−\left({n}+\mathrm{1}\right)} \\ $$$${h}^{\left(\mathrm{2}\right)} \left({x}\right)\:=\left(−\mathrm{1}\right)^{\mathrm{2}} \:\boldsymbol{{n}}\left(\boldsymbol{{n}}+\mathrm{1}\right)\:\left(\boldsymbol{{t}}+\mathrm{2}\right)^{−\left(\boldsymbol{{n}}+\mathrm{2}\right)} \\ $$$$\boldsymbol{{h}}^{\left(\boldsymbol{{k}}\right)} \left({x}\right)=\:\left(−\mathrm{1}\right)^{{k}} \:{n}\left({n}+\mathrm{1}\right).....\left({n}+{k}−\mathrm{1}\right)\left({t}+\mathrm{2}\right)^{−\left({n}+{k}\right)} \\ $$$${h}^{\left({k}\right)} \left(\mathrm{0}\right)\:=\left(−\mathrm{1}\right)^{{k}} {n}\left({n}+\mathrm{1}\right).....\left({n}+{k}−\mathrm{1}\right)\:\mathrm{2}^{−\left({n}+{k}\right)} \\ $$$$\Rightarrow\:{h}\left({x}\right)\:=\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:\:\:\:\:\frac{\left(−\mathrm{1}\right)^{{k}} \:{n}\left({n}+\mathrm{1}\right)....\left({n}+{k}−\mathrm{1}\right)}{{k}!\:\mathrm{2}^{{n}+{k}} }\:{x}^{{k}} \\ $$$$+\:\frac{{x}^{{n}} }{{n}!}\:\xi\left({x}\right) \\ $$

Commented by abdo mathsup 649 cc last updated on 07/May/18

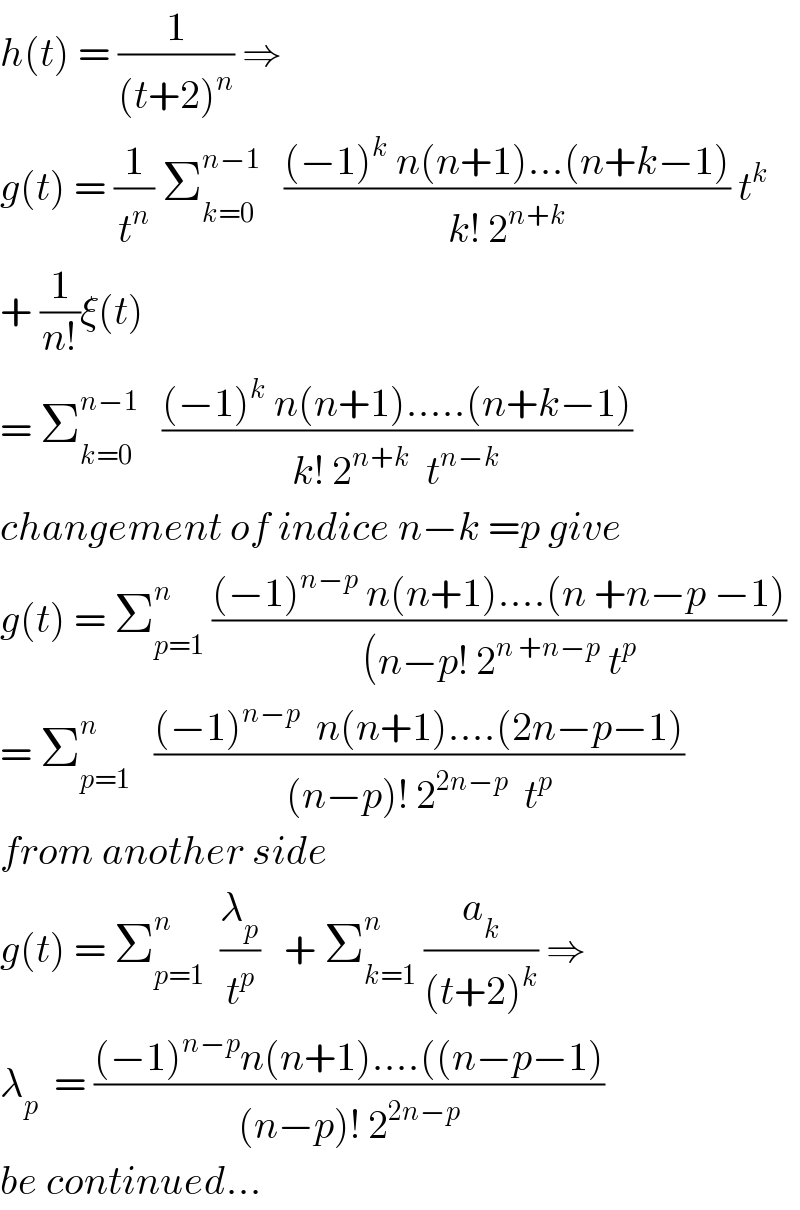
h(t) = (1/((t+2)^n )) ⇒ g(t) = (1/t^n ) Σ_(k=0) ^(n−1) (((−1)^k n(n+1)...(n+k−1))/(k! 2^(n+k) )) t^k + (1/(n!))ξ(t) = Σ_(k=0) ^(n−1) (((−1)^k n(n+1).....(n+k−1))/(k! 2^(n+k) t^(n−k) )) changement of indice n−k =p give g(t) = Σ_(p=1) ^n (((−1)^(n−p) n(n+1)....(n +n−p −1))/((n−p! 2^(n +n−p) t^p )) = Σ_(p=1) ^n (((−1)^(n−p) n(n+1)....(2n−p−1))/((n−p)! 2^(2n−p) t^p )) from another side g(t) = Σ_(p=1) ^n (λ_p /t^p ) + Σ_(k=1) ^n (a_k /((t+2)^k )) ⇒ λ_p = (((−1)^(n−p) n(n+1)....((n−p−1))/((n−p)! 2^(2n−p) )) be continued...

$${h}\left({t}\right)\:=\:\frac{\mathrm{1}}{\left({t}+\mathrm{2}\right)^{{n}} }\:\Rightarrow \\ $$$${g}\left({t}\right)\:=\:\frac{\mathrm{1}}{{t}^{{n}} }\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:\:\frac{\left(−\mathrm{1}\right)^{{k}} \:{n}\left({n}+\mathrm{1}\right)...\left({n}+{k}−\mathrm{1}\right)}{{k}!\:\mathrm{2}^{{n}+{k}} }\:{t}^{{k}} \\ $$$$+\:\frac{\mathrm{1}}{{n}!}\xi\left({t}\right)\: \\ $$$$=\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:\:\frac{\left(−\mathrm{1}\right)^{{k}} \:{n}\left({n}+\mathrm{1}\right).....\left({n}+{k}−\mathrm{1}\right)}{{k}!\:\mathrm{2}^{{n}+{k}} \:\:{t}^{{n}−{k}} } \\ $$$${changement}\:{of}\:{indice}\:{n}−{k}\:={p}\:{give} \\ $$$${g}\left({t}\right)\:=\:\sum_{{p}=\mathrm{1}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{{n}−{p}} \:{n}\left({n}+\mathrm{1}\right)....\left({n}\:+{n}−{p}\:−\mathrm{1}\right)}{\left({n}−{p}!\:\mathrm{2}^{{n}\:+{n}−{p}} \:{t}^{{p}} \right.} \\ $$$$=\:\sum_{{p}=\mathrm{1}} ^{{n}} \:\:\:\frac{\left(−\mathrm{1}\right)^{{n}−{p}} \:\:{n}\left({n}+\mathrm{1}\right)....\left(\mathrm{2}{n}−{p}−\mathrm{1}\right)}{\left({n}−{p}\right)!\:\mathrm{2}^{\mathrm{2}{n}−{p}} \:\:{t}^{{p}} } \\ $$$${from}\:{another}\:{side} \\ $$$${g}\left({t}\right)\:=\:\sum_{{p}=\mathrm{1}} ^{{n}} \:\:\frac{\lambda_{{p}} }{{t}^{{p}} }\:\:\:+\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{{a}_{{k}} }{\left({t}+\mathrm{2}\right)^{{k}} }\:\Rightarrow \\ $$$$\lambda_{{p}} \:\:=\:\frac{\left(−\mathrm{1}\right)^{{n}−{p}} {n}\left({n}+\mathrm{1}\right)....\left(\left({n}−{p}−\mathrm{1}\right)\right.}{\left({n}−{p}\right)!\:\mathrm{2}^{\mathrm{2}{n}−{p}} } \\ $$$${be}\:{continued}... \\ $$

Commented by abdo mathsup 649 cc last updated on 07/May/18

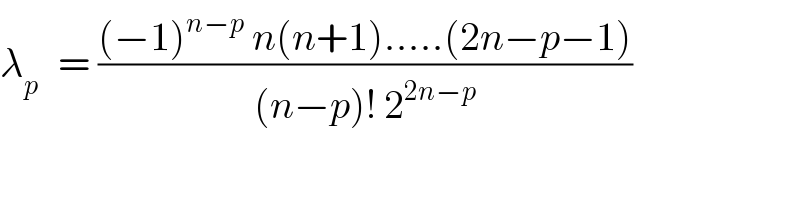
λ_(p ) = (((−1)^(n−p) n(n+1).....(2n−p−1))/((n−p)! 2^(2n−p) ))

$$\lambda_{{p}\:} \:\:=\:\frac{\left(−\mathrm{1}\right)^{{n}−{p}} \:{n}\left({n}+\mathrm{1}\right).....\left(\mathrm{2}{n}−{p}−\mathrm{1}\right)}{\left({n}−{p}\right)!\:\mathrm{2}^{\mathrm{2}{n}−{p}} } \\ $$

Commented by prof Abdo imad last updated on 07/May/18

we have F(x)= (1/((x−1)^n (x+1)^n )) now we use the changement x+1 =t ⇒ F(x)=g(t) = (1/((t−2)^n t^n )) let put h(t) =(1/((t−2)^n )) = Σ_(k=0) ^(n−1) ((h^((k)) (0))/(k!)) t^k + (t^n /(n!)) ξ(t) h^((k)) (x) =(−1)^k n(n+1)....(n+k−1) (t−2)^(−(n+k)) h^((k)) (0) =(−1)^k n(n+1).....(n+k−1)(−2)^(−(n+k)) ⇒h(t) =Σ_(k=0) ^(n−1) (((−1)^k n(n+1)....(n+k−1))/(k!(−2)^(n+k) )) t^k +(t^n /(n!))ξ(t)⇒g(t)= Σ_(k=0) ^(n−1) (((−1)^k n(n+1)...(n+k−1))/(k!(−2)^(n+k) t^(n−k) )) and we folow tbe same road to find a_k ....

$${we}\:{have}\:{F}\left({x}\right)=\:\frac{\mathrm{1}}{\left({x}−\mathrm{1}\right)^{{n}} \left({x}+\mathrm{1}\right)^{{n}} }\:{now}\:{we}\:{use} \\ $$$${the}\:{changement}\:{x}+\mathrm{1}\:={t}\:\Rightarrow \\ $$$${F}\left({x}\right)={g}\left({t}\right)\:=\:\frac{\mathrm{1}}{\left({t}−\mathrm{2}\right)^{{n}} \:{t}^{{n}} }\:{let}\:{put} \\ $$$${h}\left({t}\right)\:=\frac{\mathrm{1}}{\left({t}−\mathrm{2}\right)^{{n}} }\:=\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\frac{{h}^{\left({k}\right)} \left(\mathrm{0}\right)}{{k}!}\:{t}^{{k}} \:\:+\:\frac{{t}^{{n}} }{{n}!}\:\xi\left({t}\right) \\ $$$${h}^{\left({k}\right)} \left({x}\right)\:=\left(−\mathrm{1}\right)^{{k}} {n}\left({n}+\mathrm{1}\right)....\left({n}+{k}−\mathrm{1}\right)\:\left({t}−\mathrm{2}\right)^{−\left({n}+{k}\right)} \\ $$$${h}^{\left({k}\right)} \left(\mathrm{0}\right)\:=\left(−\mathrm{1}\right)^{{k}} \:{n}\left({n}+\mathrm{1}\right).....\left({n}+{k}−\mathrm{1}\right)\left(−\mathrm{2}\right)^{−\left({n}+{k}\right)} \\ $$$$\Rightarrow{h}\left({t}\right)\:=\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:\:\frac{\left(−\mathrm{1}\right)^{{k}} \:{n}\left({n}+\mathrm{1}\right)....\left({n}+{k}−\mathrm{1}\right)}{{k}!\left(−\mathrm{2}\right)^{{n}+{k}} }\:{t}^{{k}} \\ $$$$+\frac{{t}^{{n}} }{{n}!}\xi\left({t}\right)\Rightarrow{g}\left({t}\right)=\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\frac{\left(−\mathrm{1}\right)^{{k}} \:{n}\left({n}+\mathrm{1}\right)...\left({n}+{k}−\mathrm{1}\right)}{{k}!\left(−\mathrm{2}\right)^{{n}+{k}} \:{t}^{{n}−{k}} } \\ $$$${and}\:{we}\:{folow}\:{tbe}\:{same}\:{road}\:{to}\:{find}\:{a}_{{k}} \:.... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com