Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 34044 by NECx last updated on 29/Apr/18

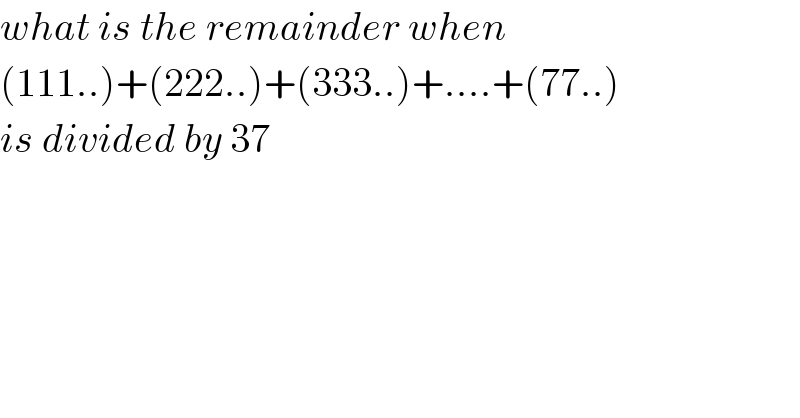
what is the remainder when (111..)+(222..)+(333..)+....+(77..) is divided by 37

$${what}\:{is}\:{the}\:{remainder}\:{when}\: \\ $$$$\left(\mathrm{111}..\right)+\left(\mathrm{222}..\right)+\left(\mathrm{333}..\right)+....+\left(\mathrm{77}..\right) \\ $$$${is}\:{divided}\:{by}\:\mathrm{37} \\ $$

Commented by Rasheed.Sindhi last updated on 30/Apr/18

N=(111..)+(222..)+(333..)+....+(77..) =1(111...)+2(111..)+3(111...)...+7(111..) =(1+2+3+...+7)(11...) =28×111... Let 111...is of n-digits number. For n=1 N=28.1=28, If 28 is divided by 37 the remainder is 28 ....... .... If n=3k,the remainder is 0 If n=3k+1,the remainder is 28 If n=3k+2,the remainder is 12 The remainders : 0,28,12

$$\mathrm{N}=\left(\mathrm{111}..\right)+\left(\mathrm{222}..\right)+\left(\mathrm{333}..\right)+....+\left(\mathrm{77}..\right) \\ $$$$ \\ $$$$=\mathrm{1}\left(\mathrm{111}...\right)+\mathrm{2}\left(\mathrm{111}..\right)+\mathrm{3}\left(\mathrm{111}...\right)...+\mathrm{7}\left(\mathrm{111}..\right) \\ $$$$=\left(\mathrm{1}+\mathrm{2}+\mathrm{3}+...+\mathrm{7}\right)\left(\mathrm{11}...\right) \\ $$$$=\mathrm{28}×\mathrm{111}... \\ $$$$\mathrm{Let}\:\mathrm{111}...\mathrm{is}\:\mathrm{of}\:\mathrm{n}-\mathrm{digits}\:\mathrm{number}. \\ $$$$\mathrm{For}\:\mathrm{n}=\mathrm{1} \\ $$$$\mathrm{N}=\mathrm{28}.\mathrm{1}=\mathrm{28},\: \\ $$$$\mathrm{If}\:\mathrm{28}\:\mathrm{is}\:\mathrm{divided}\:\mathrm{by}\:\mathrm{37}\:\mathrm{the}\:\mathrm{remainder}\:\mathrm{is}\:\mathrm{28} \\ $$$$....... \\ $$$$.... \\ $$$$\mathrm{If}\:\mathrm{n}=\mathrm{3k},\mathrm{the}\:\mathrm{remainder}\:\mathrm{is}\:\:\mathrm{0} \\ $$$$\mathrm{If}\:\mathrm{n}=\mathrm{3k}+\mathrm{1},\mathrm{the}\:\mathrm{remainder}\:\mathrm{is}\:\mathrm{28} \\ $$$$\mathrm{If}\:\mathrm{n}=\mathrm{3k}+\mathrm{2},\mathrm{the}\:\mathrm{remainder}\:\mathrm{is}\:\mathrm{12} \\ $$$$\mathrm{The}\:\mathrm{remainders}\::\:\mathrm{0},\mathrm{28},\mathrm{12} \\ $$

Commented by NECx last updated on 30/Apr/18

thank you so much buddy

$${thank}\:{you}\:{so}\:{much}\:{buddy} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 30/Apr/18

(111...)+(222...)+(333...)+....+(777...) (111...)+2(111...)+3(111...)+...+7(111...) let value of (111...) say=t t(1+2+3+...+7) t(28) now let us find the value of (111...upto n ) then put n→∞ (111...upto n terms) 1+10+10^2 +10^3 +.... (((10^n −1))/(10−1)) 28t (37−9)t (37−9)(((10^n −1))/9) ((37)/9)(10^n −1)+(1−10^n ) when devided by 37 first part is divisble by 37 remaining is remainder under the condktion n→∞ pls recheck the question pls

$$\left(\mathrm{111}...\right)+\left(\mathrm{222}...\right)+\left(\mathrm{333}...\right)+....+\left(\mathrm{777}...\right) \\ $$$$\left(\mathrm{111}...\right)+\mathrm{2}\left(\mathrm{111}...\right)+\mathrm{3}\left(\mathrm{111}...\right)+...+\mathrm{7}\left(\mathrm{111}...\right) \\ $$$${let}\:{value}\:{of}\:\left(\mathrm{111}...\right)\:{say}={t} \\ $$$${t}\left(\mathrm{1}+\mathrm{2}+\mathrm{3}+...+\mathrm{7}\right) \\ $$$${t}\left(\mathrm{28}\right) \\ $$$${now}\:{let}\:{us}\:{find}\:{the}\:{value}\:{of}\:\left(\mathrm{111}...{upto}\:{n}\:\right)\:{then} \\ $$$${put}\:{n}\rightarrow\infty \\ $$$$\left(\mathrm{111}...{upto}\:{n}\:{terms}\right) \\ $$$$\mathrm{1}+\mathrm{10}+\mathrm{10}^{\mathrm{2}} +\mathrm{10}^{\mathrm{3}} +.... \\ $$$$\frac{\left(\mathrm{10}^{{n}} −\mathrm{1}\right)}{\mathrm{10}−\mathrm{1}} \\ $$$$\mathrm{28}{t} \\ $$$$\left(\mathrm{37}−\mathrm{9}\right){t} \\ $$$$\left(\mathrm{37}−\mathrm{9}\right)\frac{\left(\mathrm{10}^{{n}} −\mathrm{1}\right)}{\mathrm{9}} \\ $$$$\frac{\mathrm{37}}{\mathrm{9}}\left(\mathrm{10}^{{n}} −\mathrm{1}\right)+\left(\mathrm{1}−\mathrm{10}^{{n}} \right) \\ $$$${when}\:{devided}\:{by}\:\mathrm{37}\:{first}\:{part}\:{is}\:{divisble}\:{by}\:\mathrm{37} \\ $$$${remaining}\:{is}\:{remainder}\:{under}\:{the}\:{condktion}\:{n}\rightarrow\infty \\ $$$${pls}\:{recheck}\:{the}\:{question}\:{pls} \\ $$$$ \\ $$

Commented by NECx last updated on 30/Apr/18

wow.... lemme check it..Really I love what you just did.Thanks

$${wow}....\:{lemme}\:{check}\:{it}..{Really} \\ $$$${I}\:{love}\:{what}\:{you}\:{just}\:{did}.{Thanks} \\ $$

Commented by Rasheed.Sindhi last updated on 30/Apr/18

The remainder should be positive,whereas 1−10^n is negative for n>0

$$\mathrm{The}\:\mathrm{remainder}\:\mathrm{should}\:\mathrm{be}\:\mathrm{positive},\mathrm{whereas} \\ $$$$\mathrm{1}−\mathrm{10}^{\mathrm{n}} \:\mathrm{is}\:\mathrm{negative}\:\mathrm{for}\:\mathrm{n}>\mathrm{0} \\ $$

Answered by 5a3k last updated on 30/Apr/18

[(111..)+(222..)+(333..)+...+(777..)] ((37[3+6+9+...+21])/(37)) 3+6+9+....+21 7/2[2×3+(7−1)3] 84

$$\left[\left(\mathrm{111}..\right)+\left(\mathrm{222}..\right)+\left(\mathrm{333}..\right)+...+\left(\mathrm{777}..\right)\right] \\ $$$$\frac{\mathrm{37}\left[\mathrm{3}+\mathrm{6}+\mathrm{9}+...+\mathrm{21}\right]}{\mathrm{37}} \\ $$$$\mathrm{3}+\mathrm{6}+\mathrm{9}+....+\mathrm{21} \\ $$$$\mathrm{7}/\mathrm{2}\left[\mathrm{2}×\mathrm{3}+\left(\mathrm{7}−\mathrm{1}\right)\mathrm{3}\right] \\ $$$$\mathrm{84} \\ $$

Commented by NECx last updated on 30/Apr/18

not clear please

$${not}\:{clear}\:{please} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com