Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 3410 by 123456 last updated on 13/Dec/15

lets (u,v,w)∈C^3 such that uvw≠0, proof that (or give a counter example) (v/u)=(w/v)∧∣u∣=∣v∣=∣w∣∧u≠w⇒u+v+w=0

$$\mathrm{lets}\:\left({u},{v},{w}\right)\in\mathbb{C}^{\mathrm{3}} \:\mathrm{such}\:\mathrm{that}\:{uvw}\neq\mathrm{0},\:\mathrm{proof} \\ $$$$\mathrm{that}\:\left(\mathrm{or}\:\mathrm{give}\:\mathrm{a}\:\mathrm{counter}\:\mathrm{example}\right) \\ $$$$\frac{{v}}{{u}}=\frac{{w}}{{v}}\wedge\mid{u}\mid=\mid{v}\mid=\mid{w}\mid\wedge{u}\neq{w}\Rightarrow{u}+{v}+{w}=\mathrm{0} \\ $$

Commented by RasheedSindhi last updated on 13/Dec/15

What is meant by u,v,w∈C^3 ?

$$\mathcal{W}{hat}\:{is}\:{meant}\:{by}\:{u},{v},{w}\in\mathbb{C}^{\mathrm{3}} \:? \\ $$

Commented by 123456 last updated on 13/Dec/15

u∈C∧v∈C∧w∈C

$${u}\in\mathbb{C}\wedge{v}\in\mathbb{C}\wedge{w}\in\mathbb{C} \\ $$

Commented by RasheedSindhi last updated on 13/Dec/15

Do you mean Given:(u,v,w)∈C^3 ∧ uvw≠0 To prove:(v/u)=(w/v)∧∣u∣=∣v∣=∣w∣∧u≠w⇒u+v+w=0?

$${Do}\:{you}\:{mean} \\ $$$${Given}:\left({u},{v},{w}\right)\in\mathbb{C}^{\mathrm{3}} \:\wedge\:{uvw}\neq\mathrm{0} \\ $$$$\:\:{To}\:{prove}:\frac{{v}}{{u}}=\frac{{w}}{{v}}\wedge\mid{u}\mid=\mid{v}\mid=\mid{w}\mid\wedge{u}\neq{w}\Rightarrow{u}+{v}+{w}=\mathrm{0}? \\ $$$$ \\ $$

Commented by 123456 last updated on 13/Dec/15

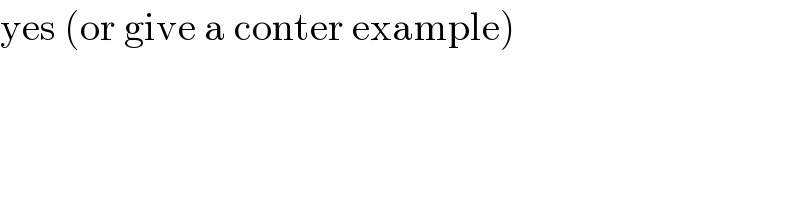
yes (or give a conter example)

$$\mathrm{yes}\:\left(\mathrm{or}\:\mathrm{give}\:\mathrm{a}\:\mathrm{conter}\:\mathrm{example}\right) \\ $$

Commented by Yozzi last updated on 13/Dec/15

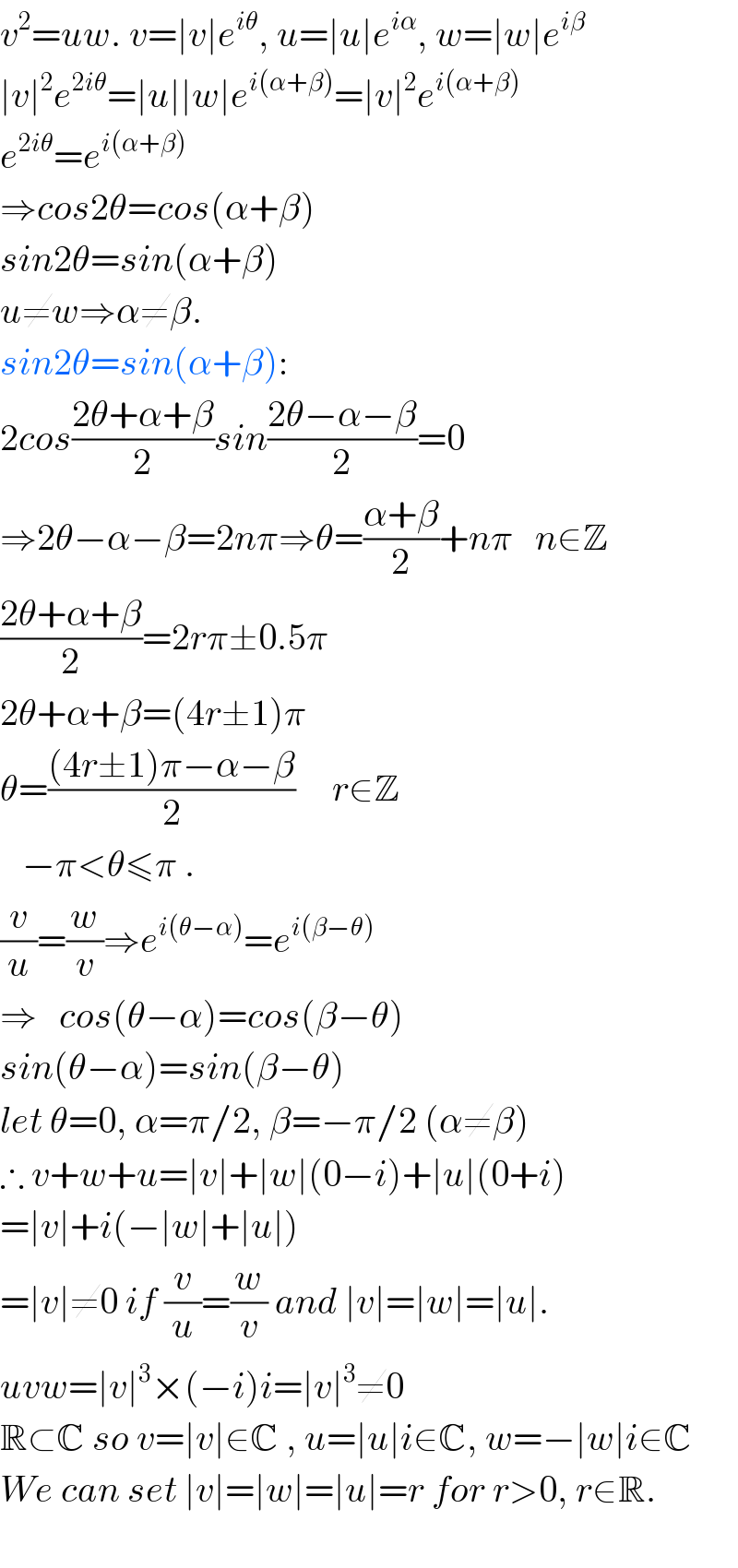
v^2 =uw. v=∣v∣e^(iθ) , u=∣u∣e^(iα) , w=∣w∣e^(iβ) ∣v∣^2 e^(2iθ) =∣u∣∣w∣e^(i(α+β)) =∣v∣^2 e^(i(α+β)) e^(2iθ) =e^(i(α+β)) ⇒cos2θ=cos(α+β) sin2θ=sin(α+β) u≠w⇒α≠β. sin2θ=sin(α+β): 2cos((2θ+α+β)/2)sin((2θ−α−β)/2)=0 ⇒2θ−α−β=2nπ⇒θ=((α+β)/2)+nπ n∈Z ((2θ+α+β)/2)=2rπ±0.5π 2θ+α+β=(4r±1)π θ=(((4r±1)π−α−β)/2) r∈Z −π<θ≤π . (v/u)=(w/v)⇒e^(i(θ−α)) =e^(i(β−θ)) ⇒ cos(θ−α)=cos(β−θ) sin(θ−α)=sin(β−θ) let θ=0, α=π/2, β=−π/2 (α≠β) ∴ v+w+u=∣v∣+∣w∣(0−i)+∣u∣(0+i) =∣v∣+i(−∣w∣+∣u∣) =∣v∣≠0 if (v/u)=(w/v) and ∣v∣=∣w∣=∣u∣. uvw=∣v∣^3 ×(−i)i=∣v∣^3 ≠0 R⊂C so v=∣v∣∈C , u=∣u∣i∈C, w=−∣w∣i∈C We can set ∣v∣=∣w∣=∣u∣=r for r>0, r∈R.

$${v}^{\mathrm{2}} ={uw}.\:{v}=\mid{v}\mid{e}^{{i}\theta} ,\:{u}=\mid{u}\mid{e}^{{i}\alpha} ,\:{w}=\mid{w}\mid{e}^{{i}\beta} \\ $$$$\mid{v}\mid^{\mathrm{2}} {e}^{\mathrm{2}{i}\theta} =\mid{u}\mid\mid{w}\mid{e}^{{i}\left(\alpha+\beta\right)} =\mid{v}\mid^{\mathrm{2}} {e}^{{i}\left(\alpha+\beta\right)} \\ $$$${e}^{\mathrm{2}{i}\theta} ={e}^{{i}\left(\alpha+\beta\right)} \\ $$$$\Rightarrow{cos}\mathrm{2}\theta={cos}\left(\alpha+\beta\right) \\ $$$${sin}\mathrm{2}\theta={sin}\left(\alpha+\beta\right) \\ $$$${u}\neq{w}\Rightarrow\alpha\neq\beta.\: \\ $$$${sin}\mathrm{2}\theta={sin}\left(\alpha+\beta\right): \\ $$$$\mathrm{2}{cos}\frac{\mathrm{2}\theta+\alpha+\beta}{\mathrm{2}}{sin}\frac{\mathrm{2}\theta−\alpha−\beta}{\mathrm{2}}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}\theta−\alpha−\beta=\mathrm{2}{n}\pi\Rightarrow\theta=\frac{\alpha+\beta}{\mathrm{2}}+{n}\pi\:\:\:{n}\in\mathbb{Z} \\ $$$$\frac{\mathrm{2}\theta+\alpha+\beta}{\mathrm{2}}=\mathrm{2}{r}\pi\pm\mathrm{0}.\mathrm{5}\pi \\ $$$$\mathrm{2}\theta+\alpha+\beta=\left(\mathrm{4}{r}\pm\mathrm{1}\right)\pi \\ $$$$\theta=\frac{\left(\mathrm{4}{r}\pm\mathrm{1}\right)\pi−\alpha−\beta}{\mathrm{2}}\:\:\:\:\:{r}\in\mathbb{Z} \\ $$$$\:\:\:−\pi<\theta\leqslant\pi\:. \\ $$$$\frac{{v}}{{u}}=\frac{{w}}{{v}}\Rightarrow{e}^{{i}\left(\theta−\alpha\right)} ={e}^{{i}\left(\beta−\theta\right)} \\ $$$$\Rightarrow\:\:\:{cos}\left(\theta−\alpha\right)={cos}\left(\beta−\theta\right) \\ $$$${sin}\left(\theta−\alpha\right)={sin}\left(\beta−\theta\right) \\ $$$${let}\:\theta=\mathrm{0},\:\alpha=\pi/\mathrm{2},\:\beta=−\pi/\mathrm{2}\:\left(\alpha\neq\beta\right) \\ $$$$\therefore\:{v}+{w}+{u}=\mid{v}\mid+\mid{w}\mid\left(\mathrm{0}−{i}\right)+\mid{u}\mid\left(\mathrm{0}+{i}\right) \\ $$$$=\mid{v}\mid+{i}\left(−\mid{w}\mid+\mid{u}\mid\right) \\ $$$$=\mid{v}\mid\neq\mathrm{0}\:{if}\:\frac{{v}}{{u}}=\frac{{w}}{{v}}\:{and}\:\mid{v}\mid=\mid{w}\mid=\mid{u}\mid. \\ $$$${uvw}=\mid{v}\mid^{\mathrm{3}} ×\left(−{i}\right){i}=\mid{v}\mid^{\mathrm{3}} \neq\mathrm{0} \\ $$$$\mathbb{R}\subset\mathbb{C}\:{so}\:{v}=\mid{v}\mid\in\mathbb{C}\:,\:{u}=\mid{u}\mid{i}\in\mathbb{C},\:{w}=−\mid{w}\mid{i}\in\mathbb{C} \\ $$$${We}\:{can}\:{set}\:\mid{v}\mid=\mid{w}\mid=\mid{u}\mid={r}\:{for}\:{r}>\mathrm{0},\:{r}\in\mathbb{R}. \\ $$$$ \\ $$

Commented by Yozzii last updated on 13/Dec/15

Testing new feature

$${Testing}\:{new}\:{feature} \\ $$

Answered by prakash jain last updated on 13/Dec/15

Counter Example from Yozzi′s comment a,−ai,ai

$$\mathrm{Counter}\:\mathrm{Example}\:\mathrm{from}\:\mathrm{Yozzi}'\mathrm{s}\:\mathrm{comment} \\ $$$${a},−{ai},{ai} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com