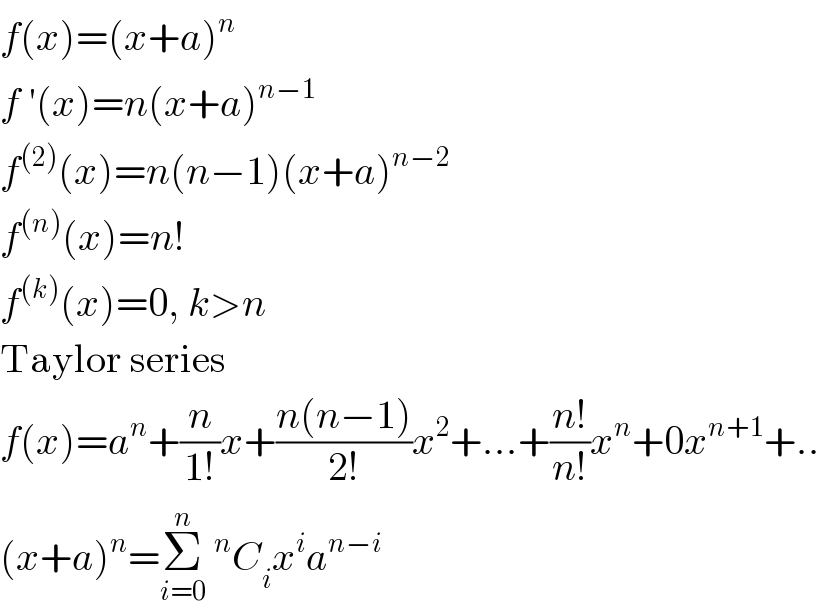Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 3411 by Filup last updated on 13/Dec/15

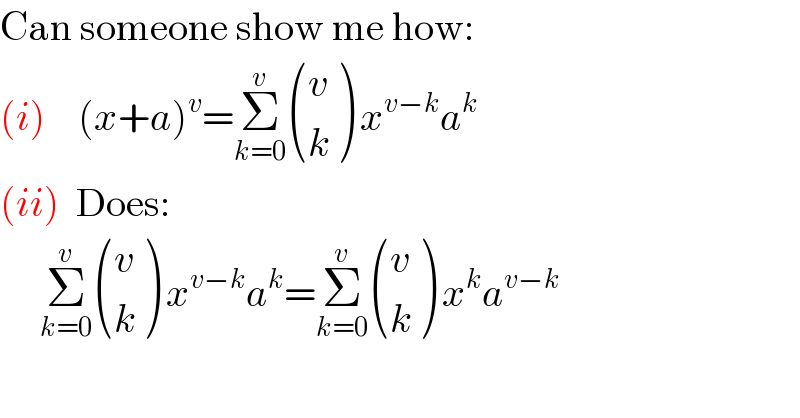
Can someone show me how: (i) (x+a)^v =Σ_(k=0) ^v ((v),(k) ) x^(v−k) a^k (ii) Does: Σ_(k=0) ^v ((v),(k) ) x^(v−k) a^k =Σ_(k=0) ^v ((v),(k) ) x^k a^(v−k)

$$\mathrm{Can}\:\mathrm{someone}\:\mathrm{show}\:\mathrm{me}\:\mathrm{how}: \\ $$$$\left({i}\right)\:\:\:\:\left({x}+{a}\right)^{{v}} =\underset{{k}=\mathrm{0}} {\overset{{v}} {\sum}}\begin{pmatrix}{{v}}\\{{k}}\end{pmatrix}\:{x}^{{v}−{k}} {a}^{{k}} \\ $$$$\left({ii}\right)\:\:\mathrm{Does}: \\ $$$$\:\:\:\:\:\underset{{k}=\mathrm{0}} {\overset{{v}} {\sum}}\begin{pmatrix}{{v}}\\{{k}}\end{pmatrix}\:{x}^{{v}−{k}} {a}^{{k}} =\underset{{k}=\mathrm{0}} {\overset{{v}} {\sum}}\begin{pmatrix}{{v}}\\{{k}}\end{pmatrix}\:{x}^{{k}} {a}^{{v}−{k}} \\ $$

Commented by RasheedSindhi last updated on 13/Dec/15

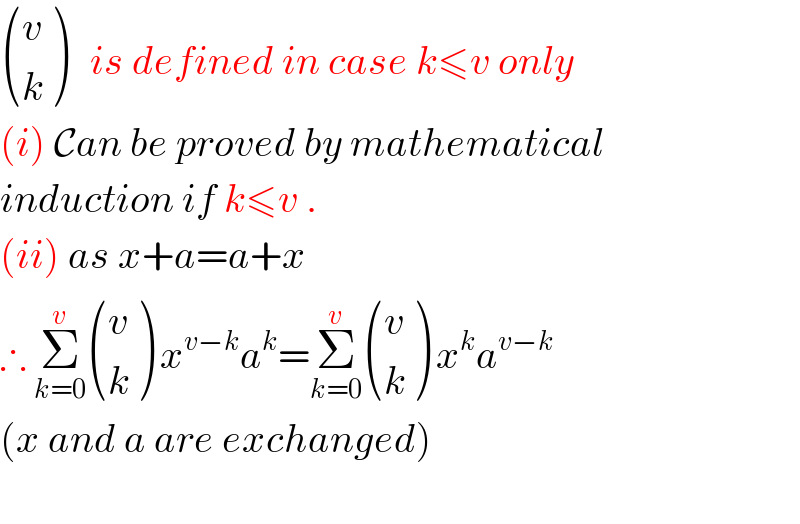
((v),(k) ) is defined in case k≤v only (i) Can be proved by mathematical induction if k≤v . (ii) as x+a=a+x ∴ Σ_(k=0) ^(v) ((v),(k) ) x^(v−k) a^k =Σ_(k=0) ^v ((v),(k) ) x^k a^(v−k) (x and a are exchanged)

$$\begin{pmatrix}{{v}}\\{{k}}\end{pmatrix}\:\:\:{is}\:{defined}\:{in}\:{case}\:{k}\leqslant{v}\:{only} \\ $$$$\left({i}\right)\:\mathcal{C}{an}\:{be}\:{proved}\:{by}\:{mathematical} \\ $$$${induction}\:{if}\:{k}\leqslant{v}\:. \\ $$$$\left({ii}\right)\:{as}\:{x}+{a}={a}+{x} \\ $$$$\therefore\:\overset{{v}} {\underset{{k}=\mathrm{0}} {\sum}}\begin{pmatrix}{{v}}\\{{k}}\end{pmatrix}\:{x}^{{v}−{k}} {a}^{{k}} =\underset{{k}=\mathrm{0}} {\overset{{v}} {\sum}}\begin{pmatrix}{{v}}\\{{k}}\end{pmatrix}\:{x}^{{k}} {a}^{{v}−{k}} \\ $$$$\left({x}\:{and}\:{a}\:{are}\:{exchanged}\right) \\ $$$$ \\ $$

Commented by Filup last updated on 13/Dec/15

Thanks. I thought as much for (ii). I don′t know anything about mathematical induction.

$$\mathrm{Thanks}.\:\mathrm{I}\:\mathrm{thought}\:\mathrm{as}\:\mathrm{much}\:\mathrm{for}\:\left({ii}\right). \\ $$$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{know}\:\mathrm{anything}\:\mathrm{about}\: \\ $$$$\mathrm{mathematical}\:\mathrm{induction}. \\ $$

Commented by 123456 last updated on 13/Dec/15

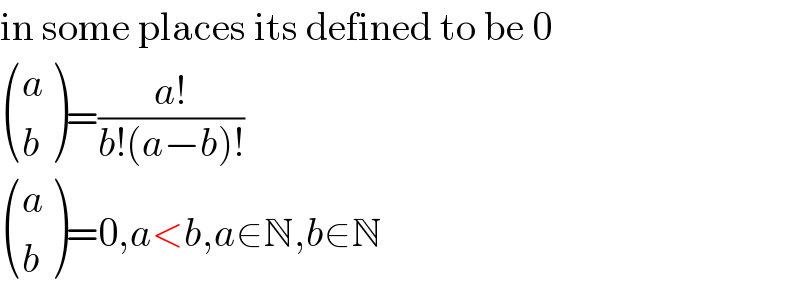
in some places its defined to be 0 ((a),(b) )=((a!)/(b!(a−b)!)) ((a),(b) )=0,a<b,a∈N,b∈N

$$\mathrm{in}\:\mathrm{some}\:\mathrm{places}\:\mathrm{its}\:\mathrm{defined}\:\mathrm{to}\:\mathrm{be}\:\mathrm{0} \\ $$$$\begin{pmatrix}{{a}}\\{{b}}\end{pmatrix}=\frac{{a}!}{{b}!\left({a}−{b}\right)!} \\ $$$$\begin{pmatrix}{{a}}\\{{b}}\end{pmatrix}=\mathrm{0},{a}<{b},{a}\in\mathbb{N},{b}\in\mathbb{N} \\ $$

Commented by RasheedSindhi last updated on 13/Dec/15

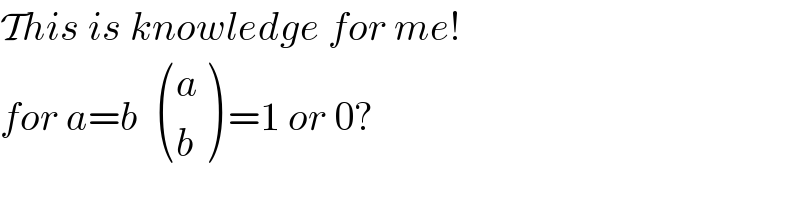
This is knowledge for me! for a=b ((a),(b) ) =1 or 0?

$$\mathcal{T}{his}\:{is}\:{knowledge}\:{for}\:{me}! \\ $$$${for}\:{a}={b}\:\:\begin{pmatrix}{{a}}\\{{b}}\end{pmatrix}\:=\mathrm{1}\:{or}\:\mathrm{0}? \\ $$

Commented by 123456 last updated on 13/Dec/15

1, i aciddentaly write it wrong

$$\mathrm{1},\:\mathrm{i}\:\mathrm{aciddentaly}\:\mathrm{write}\:\mathrm{it}\:\mathrm{wrong} \\ $$

Commented by Filup last updated on 13/Dec/15

((a),(a) ) = ((a!)/((a−a)! a!)) =(1/1)

$$\begin{pmatrix}{{a}}\\{{a}}\end{pmatrix}\:=\:\frac{{a}!}{\left({a}−{a}\right)!\:{a}!} \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}} \\ $$

Commented by Yozzi last updated on 13/Dec/15

There is also a combinatorical approach to proving the Binomial theorem.

$${There}\:{is}\:{also}\:{a}\:{combinatorical} \\ $$$${approach}\:{to}\:{proving}\:{the}\:{Binomial} \\ $$$${theorem}. \\ $$

Commented by 123456 last updated on 13/Dec/15

for curiosity there some reaction to take ((a),(b) )=0 a∈N∧b∈Z∧(b<0∨b>a) we have ((a),(b) )=((a!)/(b!(a−b)!))=((Γ(a+1))/(Γ(b+1)Γ(a−b+1))) x!=Γ(x+1) the poles of Γ(x) are {...,−2,−1,0} so the poles of x! are {...,−3,−2,−1} so if b<0 we get a pole at b! if a<b⇒a−b<0 we get a pole at (a−b)! so its act like ((a!)/(x!(a−x)!))=(k_1 /(±∞k_2 ))=0 however this is if we take the result of limit as (a,b) lim_((x,y)→(a,b)) ((x),(y) ) you can also compute it for non intergers by gamma function ((1),((1/2)) )=((1!)/([(1/2)!]^2 ))=(4/π)

$$\mathrm{for}\:\mathrm{curiosity}\:\mathrm{there}\:\mathrm{some}\:\mathrm{reaction}\:\mathrm{to}\:\mathrm{take} \\ $$$$\begin{pmatrix}{{a}}\\{{b}}\end{pmatrix}=\mathrm{0}\:\:\:\:{a}\in\mathbb{N}\wedge{b}\in\mathbb{Z}\wedge\left({b}<\mathrm{0}\vee{b}>{a}\right) \\ $$$$\mathrm{we}\:\mathrm{have} \\ $$$$\begin{pmatrix}{{a}}\\{{b}}\end{pmatrix}=\frac{{a}!}{{b}!\left({a}−{b}\right)!}=\frac{\Gamma\left({a}+\mathrm{1}\right)}{\Gamma\left({b}+\mathrm{1}\right)\Gamma\left({a}−{b}+\mathrm{1}\right)} \\ $$$${x}!=\Gamma\left({x}+\mathrm{1}\right) \\ $$$$\mathrm{the}\:\mathrm{poles}\:\mathrm{of}\:\Gamma\left({x}\right)\:\mathrm{are}\:\left\{...,−\mathrm{2},−\mathrm{1},\mathrm{0}\right\} \\ $$$$\mathrm{so}\:\mathrm{the}\:\mathrm{poles}\:\mathrm{of}\:{x}!\:\mathrm{are}\:\left\{...,−\mathrm{3},−\mathrm{2},−\mathrm{1}\right\} \\ $$$$\mathrm{so} \\ $$$$\mathrm{if}\:{b}<\mathrm{0}\:\mathrm{we}\:\mathrm{get}\:\mathrm{a}\:\mathrm{pole}\:\mathrm{at}\:{b}! \\ $$$$\mathrm{if}\:{a}<{b}\Rightarrow{a}−{b}<\mathrm{0}\:\mathrm{we}\:\mathrm{get}\:\mathrm{a}\:\mathrm{pole}\:\mathrm{at}\:\left({a}−{b}\right)! \\ $$$$\mathrm{so}\:\mathrm{its}\:\mathrm{act}\:\mathrm{like} \\ $$$$\frac{{a}!}{{x}!\left({a}−{x}\right)!}=\frac{{k}_{\mathrm{1}} }{\pm\infty{k}_{\mathrm{2}} }=\mathrm{0} \\ $$$$\mathrm{however}\:\mathrm{this}\:\mathrm{is}\:\mathrm{if}\:\mathrm{we}\:\mathrm{take}\:\mathrm{the}\:\mathrm{result}\:\mathrm{of} \\ $$$$\mathrm{limit}\:\mathrm{as}\:\left({a},{b}\right) \\ $$$$\underset{\left({x},{y}\right)\rightarrow\left({a},{b}\right)} {\mathrm{lim}}\begin{pmatrix}{{x}}\\{{y}}\end{pmatrix} \\ $$$$\mathrm{you}\:\mathrm{can}\:\mathrm{also}\:\mathrm{compute}\:\mathrm{it}\:\mathrm{for}\:\mathrm{non}\:\mathrm{intergers}\:\mathrm{by}\:\mathrm{gamma}\:\mathrm{function} \\ $$$$\begin{pmatrix}{\mathrm{1}}\\{\mathrm{1}/\mathrm{2}}\end{pmatrix}=\frac{\mathrm{1}!}{\left[\left(\mathrm{1}/\mathrm{2}\right)!\right]^{\mathrm{2}} }=\frac{\mathrm{4}}{\pi} \\ $$

Answered by 123456 last updated on 13/Dec/15

lets shown (x+a)^n =Σ_(k=0) ^n ((n),(k) )x^(n−k) a^k n∈N base case: n=0 (x+a)^0 =1 n=1 (x+a)^1 =x+a inductive steep: assuming its truth to n, let shown to n+1 (x+a)^(n+1) =(x+a)(x+a)^n =(x+a)Σ_(k=0) ^n ((n),(k) )x^(n−k) a^k =Σ_(k=0) ^n ((n),(k) )x^(n+1−k) a^k +Σ_(k=0) ^n ((n),(k) )x^(n−k) a^(k+1) =Σ_(k=0) ^n ((n),(k) )x^(n+1−k) a^k +Σ_(k=1) ^(n+1) ((n),((k−1)) )x^(n+1−k) a^k =x^(n+1) +Σ_(k=1) ^n ((n),(k) )x^(n+1−k) a^k +Σ_(k=1) ^n ((n),((k−1)) )x^(n+1−k) a^k +a^(n+1) =x^(n+1) +Σ_(k=1) ^n ( ((n),(k) )+ ((n),((k−1)) ) )x^(n+1−k) a^k +a^(n+1) =x^(n+1) +Σ_(k=1) ^n (((n+1)),(k) )x^(n+1−k) a^k +a^(n+1) =Σ_(k=0) ^(n+1) (((n+1)),(k) )x^(n+1−k) a^k □ ((n),(k) )+ ((n),((k−1)) )= (((n+1)),(k) )

$$\mathrm{lets}\:\mathrm{shown}\:\left({x}+{a}\right)^{{n}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}{x}^{{n}−{k}} {a}^{{k}} \:\:\:{n}\in\mathbb{N} \\ $$$$\mathrm{base}\:\mathrm{case}: \\ $$$${n}=\mathrm{0} \\ $$$$\left({x}+{a}\right)^{\mathrm{0}} =\mathrm{1} \\ $$$${n}=\mathrm{1} \\ $$$$\left({x}+{a}\right)^{\mathrm{1}} ={x}+{a} \\ $$$$\mathrm{inductive}\:\mathrm{steep}: \\ $$$$\mathrm{assuming}\:\mathrm{its}\:\mathrm{truth}\:\mathrm{to}\:{n},\:\mathrm{let}\:\mathrm{shown}\:\mathrm{to} \\ $$$${n}+\mathrm{1} \\ $$$$\left({x}+{a}\right)^{{n}+\mathrm{1}} =\left({x}+{a}\right)\left({x}+{a}\right)^{{n}} \\ $$$$=\left({x}+{a}\right)\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}{x}^{{n}−{k}} {a}^{{k}} \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}{x}^{{n}+\mathrm{1}−{k}} {a}^{{k}} +\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}{x}^{{n}−{k}} {a}^{{k}+\mathrm{1}} \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}{x}^{{n}+\mathrm{1}−{k}} {a}^{{k}} +\underset{{k}=\mathrm{1}} {\overset{{n}+\mathrm{1}} {\sum}}\begin{pmatrix}{{n}}\\{{k}−\mathrm{1}}\end{pmatrix}{x}^{{n}+\mathrm{1}−{k}} {a}^{{k}} \\ $$$$={x}^{{n}+\mathrm{1}} +\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}{x}^{{n}+\mathrm{1}−{k}} {a}^{{k}} +\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{k}−\mathrm{1}}\end{pmatrix}{x}^{{n}+\mathrm{1}−{k}} {a}^{{k}} +{a}^{{n}+\mathrm{1}} \\ $$$$={x}^{{n}+\mathrm{1}} +\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}+\begin{pmatrix}{{n}}\\{{k}−\mathrm{1}}\end{pmatrix}\:\right){x}^{{n}+\mathrm{1}−{k}} {a}^{{k}} +{a}^{{n}+\mathrm{1}} \\ $$$$={x}^{{n}+\mathrm{1}} +\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}+\mathrm{1}}\\{{k}}\end{pmatrix}{x}^{{n}+\mathrm{1}−{k}} {a}^{{k}} +{a}^{{n}+\mathrm{1}} \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{{n}+\mathrm{1}} {\sum}}\begin{pmatrix}{{n}+\mathrm{1}}\\{{k}}\end{pmatrix}{x}^{{n}+\mathrm{1}−{k}} {a}^{{k}} \:\:\:\:\Box \\ $$$$\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}+\begin{pmatrix}{{n}}\\{{k}−\mathrm{1}}\end{pmatrix}=\begin{pmatrix}{{n}+\mathrm{1}}\\{{k}}\end{pmatrix} \\ $$

Commented by Yozzi last updated on 13/Dec/15

Proof of ((n),(k) )+ ((n),((k−1)) )= (((n+1)),(k) ). Suppose we a set of n distinct objects and we choose one object as a special one. Then, the number of sets of k disinct objects is the sum of the number of sets with the special object and the number of sets without the special object. Given that we already took the special object, we need k−1 objects (to add to 1 to give k objects) from n−1 objects (we already took 1 object). This occurs in (((n−1)),((k−1)) ) ways where ((p),(q) ) is the choose function ((p),(q) )=((p!)/((p−q)!q!)). The number of sets without the special object occurs in (((n−1)),(k) ) ways since we have only n−1 objects to choose k objects from if the special object is not to be part of the set. So we have ((n),(k) )= (((n−1)),((k−1)) )+ (((n−1)),(k) ) ⇒ for a group of n+1 distinct objects (((n+1)),(k) )= ((n),((k−1)) )+ ((n),(k) ). □ We can likewise show that ((n),(k) )= (((n−1)),(k) )+2 (((n−1)),((k−1)) )+ (((n−1)),((k−2)) ) , n,k∈Z^≥ n≥k.

$${Proof}\:{of}\:\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}+\begin{pmatrix}{{n}}\\{{k}−\mathrm{1}}\end{pmatrix}=\begin{pmatrix}{{n}+\mathrm{1}}\\{{k}}\end{pmatrix}. \\ $$$${Suppose}\:{we}\:{a}\:{set}\:{of}\:{n}\:{distinct}\:{objects} \\ $$$${and}\:{we}\:{choose}\:{one}\:{object}\:{as}\:{a}\:{special}\: \\ $$$${one}.\:{Then},\:{the}\:{number}\:{of}\:{sets}\:{of} \\ $$$${k}\:{disinct}\:{objects}\:{is}\:{the}\:{sum}\:{of}\:{the}\: \\ $$$${number}\:{of}\:{sets}\:{with}\:{the}\:{special}\:{object}\:{and}\: \\ $$$${the}\:{number}\:{of}\:{sets}\:{without}\:{the}\:{special} \\ $$$${object}.\: \\ $$$${Given}\:{that}\:{we}\:{already}\:{took}\:{the}\:{special} \\ $$$${object},\:{we}\:{need}\:{k}−\mathrm{1}\:{objects}\:\left({to}\:{add}\:{to}\right. \\ $$$$\left.\mathrm{1}\:{to}\:{give}\:{k}\:{objects}\right)\:{from}\:{n}−\mathrm{1}\:{objects} \\ $$$$\left({we}\:{already}\:{took}\:\mathrm{1}\:{object}\right).\:{This}\:{occurs} \\ $$$${in}\:\begin{pmatrix}{{n}−\mathrm{1}}\\{{k}−\mathrm{1}}\end{pmatrix}\:{ways}\:{where}\:\begin{pmatrix}{{p}}\\{{q}}\end{pmatrix}\:{is}\:{the}\:{choose} \\ $$$${function}\:\begin{pmatrix}{{p}}\\{{q}}\end{pmatrix}=\frac{{p}!}{\left({p}−{q}\right)!{q}!}. \\ $$$${The}\:{number}\:{of}\:{sets}\:{without}\:{the}\:{special} \\ $$$${object}\:{occurs}\:{in}\:\begin{pmatrix}{{n}−\mathrm{1}}\\{{k}}\end{pmatrix}\:{ways}\:{since} \\ $$$${we}\:{have}\:{only}\:{n}−\mathrm{1}\:{objects}\:{to}\:{choose}\:{k} \\ $$$${objects}\:{from}\:{if}\:{the}\:{special}\:{object}\:{is} \\ $$$${not}\:{to}\:{be}\:{part}\:{of}\:{the}\:{set}. \\ $$$${So}\:{we}\:{have}\: \\ $$$$\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}=\begin{pmatrix}{{n}−\mathrm{1}}\\{{k}−\mathrm{1}}\end{pmatrix}+\begin{pmatrix}{{n}−\mathrm{1}}\\{{k}}\end{pmatrix} \\ $$$$\Rightarrow\:{for}\:{a}\:{group}\:{of}\:{n}+\mathrm{1}\:{distinct}\:{objects} \\ $$$$\begin{pmatrix}{{n}+\mathrm{1}}\\{{k}}\end{pmatrix}=\begin{pmatrix}{{n}}\\{{k}−\mathrm{1}}\end{pmatrix}+\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Box \\ $$$${We}\:{can}\:{likewise}\:{show}\:{that} \\ $$$$\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}=\begin{pmatrix}{{n}−\mathrm{1}}\\{{k}}\end{pmatrix}+\mathrm{2}\begin{pmatrix}{{n}−\mathrm{1}}\\{{k}−\mathrm{1}}\end{pmatrix}+\begin{pmatrix}{{n}−\mathrm{1}}\\{{k}−\mathrm{2}}\end{pmatrix}\:,\:{n},{k}\in\mathbb{Z}^{\geqslant} \\ $$$${n}\geqslant{k}. \\ $$

Answered by Yozzi last updated on 13/Dec/15

(x+a)^v =(a{1+(x/a)})^v (x+a)^v =a^v {1+(x/a)}^v Here, I assume that v∈Z^≥ . a≠0 (Z^≥ ={non−negative integers}) The choose function is given as ((n),(r) ) as the number of ways of choosing r objects from n distinct objects. Of course we have {1+(x/a)}^v =(1+(x/a))(1+(x/a))(1+(x/a))...(1+(x/a)) (v times) Here you have v brackets with (x/a) in each of them so that powers of (x/a) can arise in a number of ways as a consequence of picking brackets to multiply with each other to give the sought after power of (x/a). ((x/a))^v : To obtain this term, you have v brackets to choose (x/a) from and this is done in ((v),(v) ) ways. So, ((x/a))^v occurs ((v),(v) ) times and thus the term in ((x/a))^v is ((v),(v) )((x/a))^v . ((x/a))^(v−1) : Here it is the case that you′d like to obtain (x/a) multiplied by itself v−1 times. You have v brackets to choose from, so that this occurs in ((v),((v−1)) ) ways. Hence, the term in ((x/a))^(v−1) is ((v),((v−1)) ) ((x/a))^(v−1) . ((x/a))^(v−2) : This term arises in ((v),((v−2)) ) ways from among the brackets, so this term is ((v),((v−2)) )((x/a))^(v−2) . Continuing on, terms in ((x/a))^2 arise in ((v),(2) ) ways, terms in (x/a) arise in ((v),(1) ) ways and terms in ((x/a))^0 arise in ((v),(0) )=1 ways from among the brackets. We hence obtain in all, (x+a)^v =a^v [ ((v),(v) )((x/a))^v + ((v),((v−1)) )((x/a))^(v−1) + ((v),((v−2)) )((x/a))^(v−2) +...+ ((v),(2) )((x/a))^2 + ((v),(1) )((x/a)) +1] (x+a)^v =a^v (Σ_(r=0) ^v ((v),(r) )x^r a^(−r) ) (x+a)^v =Σ_(r=0) ^v ((v),(r) )x^r a^(v−r) □ If one approached the proof starting with ′The number of ways of obtaining the term ((a/x))^0 from {1+(a/x)}^v (x≠0) (after writting {x+a}^v =x^v (1+(a/x))^v ) is ((v),(0) )...′ you get the equivalent expression (x+a)^v =Σ_(r=0) ^v ((v),(r) )x^(v−r) a^r .

$$\left({x}+{a}\right)^{{v}} =\left({a}\left\{\mathrm{1}+\frac{{x}}{{a}}\right\}\right)^{{v}} \\ $$$$\left({x}+{a}\right)^{{v}} ={a}^{{v}} \left\{\mathrm{1}+\frac{{x}}{{a}}\right\}^{{v}} \: \\ $$$${Here},\:{I}\:{assume}\:{that}\:{v}\in\mathbb{Z}^{\geqslant} .\:{a}\neq\mathrm{0} \\ $$$$\left(\mathbb{Z}^{\geqslant} =\left\{{non}−{negative}\:{integers}\right\}\right) \\ $$$${The}\:{choose}\:{function}\:{is}\:{given}\:{as}\:\:\begin{pmatrix}{{n}}\\{{r}}\end{pmatrix} \\ $$$${as}\:{the}\:{number}\:{of}\:{ways}\:{of}\:{choosing} \\ $$$${r}\:{objects}\:{from}\:{n}\:{distinct}\:{objects}. \\ $$$$ \\ $$$${Of}\:{course}\:{we}\:{have} \\ $$$$\left\{\mathrm{1}+\frac{{x}}{{a}}\right\}^{{v}} =\left(\mathrm{1}+\frac{{x}}{{a}}\right)\left(\mathrm{1}+\frac{{x}}{{a}}\right)\left(\mathrm{1}+\frac{{x}}{{a}}\right)...\left(\mathrm{1}+\frac{{x}}{{a}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({v}\:{times}\right) \\ $$$${Here}\:{you}\:{have}\:{v}\:{brackets}\:{with}\:\frac{{x}}{{a}}\:{in} \\ $$$${each}\:{of}\:{them}\:{so}\:{that}\:{powers}\:{of}\:\frac{{x}}{{a}}\: \\ $$$${can}\:{arise}\:{in}\:{a}\:{number}\:{of}\:{ways}\:{as}\:{a} \\ $$$${consequence}\:{of}\:{picking}\:{brackets}\:{to}\: \\ $$$${multiply}\:{with}\:{each}\:{other}\:{to}\:{give}\:{the} \\ $$$${sought}\:{after}\:{power}\:{of}\:\frac{{x}}{{a}}. \\ $$$$\left(\frac{{x}}{{a}}\right)^{{v}} :\:{To}\:{obtain}\:{this}\:{term},\:{you}\:{have} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:{v}\:{brackets}\:{to}\:{choose}\:\frac{{x}}{{a}}\:{from}\:{and} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{this}\:{is}\:{done}\:{in}\:\begin{pmatrix}{{v}}\\{{v}}\end{pmatrix}\:{ways}.\:{So}, \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\frac{{x}}{{a}}\right)^{{v}} {occurs}\:\begin{pmatrix}{{v}}\\{{v}}\end{pmatrix}\:{times}\:{and}\:{thus} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{the}\:{term}\:{in}\:\left(\frac{{x}}{{a}}\right)^{{v}} \:{is}\:\begin{pmatrix}{{v}}\\{{v}}\end{pmatrix}\left(\frac{{x}}{{a}}\right)^{{v}} . \\ $$$$\left(\frac{{x}}{{a}}\right)^{{v}−\mathrm{1}} :\:{Here}\:{it}\:{is}\:{the}\:{case}\:{that}\:{you}'{d} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{like}\:{to}\:{obtain}\:\frac{{x}}{{a}}\:{multiplied} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{by}\:{itself}\:{v}−\mathrm{1}\:{times}. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{You}\:{have}\:{v}\:{brackets}\:{to}\:{choose} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{from},\:{so}\:{that}\:{this}\:{occurs} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{in}\:\begin{pmatrix}{{v}}\\{{v}−\mathrm{1}}\end{pmatrix}\:{ways}.\:{Hence},\:{the}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{term}\:{in}\:\left(\frac{{x}}{{a}}\right)^{{v}−\mathrm{1}} \:\:{is}\:\begin{pmatrix}{{v}}\\{{v}−\mathrm{1}}\end{pmatrix}\:\left(\frac{{x}}{{a}}\right)^{{v}−\mathrm{1}} . \\ $$$$\left(\frac{{x}}{{a}}\right)^{{v}−\mathrm{2}} :\:{This}\:{term}\:{arises}\:{in}\:\begin{pmatrix}{{v}}\\{{v}−\mathrm{2}}\end{pmatrix}\:{ways} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{from}\:{among}\:{the}\:{brackets},\:{so} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{this}\:{term}\:{is}\:\begin{pmatrix}{{v}}\\{{v}−\mathrm{2}}\end{pmatrix}\left(\frac{{x}}{{a}}\right)^{{v}−\mathrm{2}} . \\ $$$${Continuing}\:{on},\:{terms}\:{in}\:\left(\frac{{x}}{{a}}\right)^{\mathrm{2}} \: \\ $$$${arise}\:{in}\:\:\begin{pmatrix}{{v}}\\{\mathrm{2}}\end{pmatrix}\:{ways},\:{terms}\:{in}\:\frac{{x}}{{a}}\:{arise} \\ $$$${in}\:\begin{pmatrix}{{v}}\\{\mathrm{1}}\end{pmatrix}\:{ways}\:{and}\:{terms}\:{in}\:\left(\frac{{x}}{{a}}\right)^{\mathrm{0}} \:{arise} \\ $$$${in}\:\begin{pmatrix}{{v}}\\{\mathrm{0}}\end{pmatrix}=\mathrm{1}\:{ways}\:{from}\:{among}\:{the}\:{brackets}. \\ $$$${We}\:{hence}\:{obtain}\:{in}\:{all}, \\ $$$$\left({x}+{a}\right)^{{v}} ={a}^{{v}} \left[\begin{pmatrix}{{v}}\\{{v}}\end{pmatrix}\left(\frac{{x}}{{a}}\right)^{{v}} +\begin{pmatrix}{{v}}\\{{v}−\mathrm{1}}\end{pmatrix}\left(\frac{{x}}{{a}}\right)^{{v}−\mathrm{1}} \right. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\begin{pmatrix}{{v}}\\{{v}−\mathrm{2}}\end{pmatrix}\left(\frac{{x}}{{a}}\right)^{{v}−\mathrm{2}} +...+\begin{pmatrix}{{v}}\\{\mathrm{2}}\end{pmatrix}\left(\frac{{x}}{{a}}\right)^{\mathrm{2}} +\begin{pmatrix}{{v}}\\{\mathrm{1}}\end{pmatrix}\left(\frac{{x}}{{a}}\right) \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{1}\right] \\ $$$$\left({x}+{a}\right)^{{v}} ={a}^{{v}} \left(\underset{{r}=\mathrm{0}} {\overset{{v}} {\sum}}\begin{pmatrix}{{v}}\\{{r}}\end{pmatrix}{x}^{{r}} {a}^{−{r}} \right) \\ $$$$\left({x}+{a}\right)^{{v}} =\underset{{r}=\mathrm{0}} {\overset{{v}} {\sum}}\begin{pmatrix}{{v}}\\{{r}}\end{pmatrix}{x}^{{r}} {a}^{{v}−{r}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Box \\ $$$${If}\:{one}\:{approached}\:{the}\:{proof}\:{starting} \\ $$$${with}\:'{The}\:{number}\:{of}\:{ways}\:{of}\:{obtaining} \\ $$$${the}\:{term}\:\left(\frac{{a}}{{x}}\right)^{\mathrm{0}} \:{from}\:\left\{\mathrm{1}+\frac{{a}}{{x}}\right\}^{{v}} \:\left({x}\neq\mathrm{0}\right) \\ $$$$\left({after}\:{writting}\:\left\{{x}+{a}\right\}^{{v}} ={x}^{{v}} \left(\mathrm{1}+\frac{{a}}{{x}}\right)^{{v}} \right) \\ $$$${is}\:\:\begin{pmatrix}{{v}}\\{\mathrm{0}}\end{pmatrix}...'\:{you}\:{get}\:{the}\:{equivalent}\: \\ $$$${expression} \\ $$$$\left({x}+{a}\right)^{{v}} =\underset{{r}=\mathrm{0}} {\overset{{v}} {\sum}}\begin{pmatrix}{{v}}\\{{r}}\end{pmatrix}{x}^{{v}−{r}} {a}^{{r}} . \\ $$

Answered by prakash jain last updated on 13/Dec/15

f(x)=(x+a)^n f ′(x)=n(x+a)^(n−1) f^((2)) (x)=n(n−1)(x+a)^(n−2) f^((n)) (x)=n! f^((k)) (x)=0, k>n Taylor series f(x)=a^n +(n/(1!))x+((n(n−1))/(2!))x^2 +...+((n!)/(n!))x^n +0x^(n+1) +.. (x+a)^n =Σ_(i=0) ^n ^n C_i x^i a^(n−i)

$${f}\left({x}\right)=\left({x}+{a}\right)^{{n}} \\ $$$${f}\:'\left({x}\right)={n}\left({x}+{a}\right)^{{n}−\mathrm{1}} \\ $$$${f}^{\left(\mathrm{2}\right)} \left({x}\right)={n}\left({n}−\mathrm{1}\right)\left({x}+{a}\right)^{{n}−\mathrm{2}} \\ $$$${f}^{\left({n}\right)} \left({x}\right)={n}! \\ $$$${f}^{\left({k}\right)} \left({x}\right)=\mathrm{0},\:{k}>{n} \\ $$$$\mathrm{Taylor}\:\mathrm{series} \\ $$$${f}\left({x}\right)={a}^{{n}} +\frac{{n}}{\mathrm{1}!}{x}+\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{2}!}{x}^{\mathrm{2}} +...+\frac{{n}!}{{n}!}{x}^{{n}} +\mathrm{0}{x}^{{n}+\mathrm{1}} +.. \\ $$$$\left({x}+{a}\right)^{{n}} =\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}\:^{{n}} {C}_{{i}} {x}^{{i}} {a}^{{n}−{i}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com