
Question and Answers Forum
Question Number 34159 by candre last updated on 01/May/18
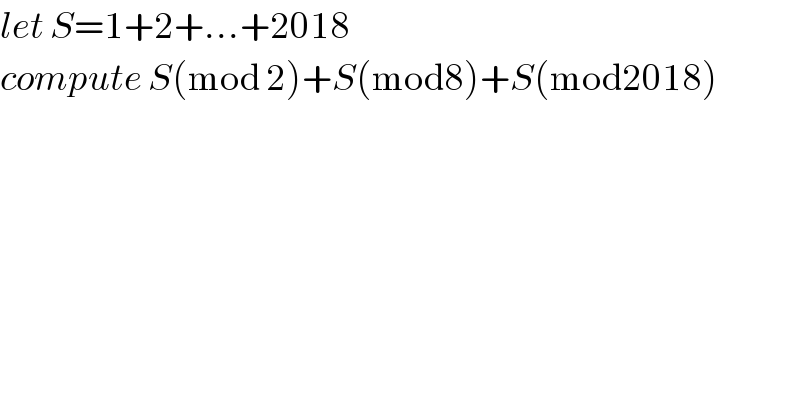
Commented by Rasheed.Sindhi last updated on 05/May/18

Answered by Rasheed.Sindhi last updated on 05/May/18
![S=1+2+...+2018; an AP:a=1,d=1,n=2018 S=(n/2)[2a+(n−1)d] S=((2018)/2)[2(1)+(2018−1)(1)] =1009[2018+1] =2018×1009+1009 ∴S(mod2018)=1009.........A −−−−−−−−−−− S=1009×2019 =(1008+1)(2018+1) =1008×2018+1008+2018+1 =1008×2019+2018+1 =2(504×2019+1009)+1 ∴S(mod 2)=1................B −−−−−− S=1009×2019 =(1009)(2000+16+3) =2000×1009+16×1009+3×1009 =2000×1009+16×1009+3000+27 =2000×1009+16×1009+3000+24+3 2000,16,3000 & 24 are divisible by 8 [Complete thousands are always divisible by8] ∴ S(mod 8)=3...............C From A,B &C S(mod 2)+S(mod 8)+S(mod 2018) =1+3+1009=1013](Q34353.png)
Commented by Rasheed.Sindhi last updated on 09/May/18

| ||
Question and Answers Forum | ||
Question Number 34159 by candre last updated on 01/May/18 | ||
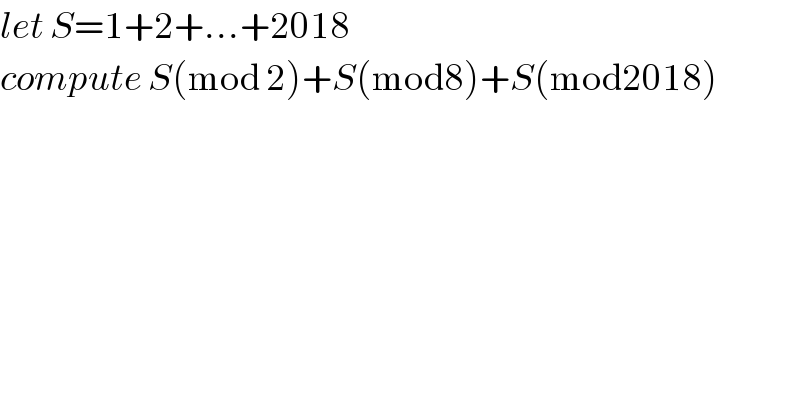 | ||
Commented by Rasheed.Sindhi last updated on 05/May/18 | ||
 | ||
Answered by Rasheed.Sindhi last updated on 05/May/18 | ||
![S=1+2+...+2018; an AP:a=1,d=1,n=2018 S=(n/2)[2a+(n−1)d] S=((2018)/2)[2(1)+(2018−1)(1)] =1009[2018+1] =2018×1009+1009 ∴S(mod2018)=1009.........A −−−−−−−−−−− S=1009×2019 =(1008+1)(2018+1) =1008×2018+1008+2018+1 =1008×2019+2018+1 =2(504×2019+1009)+1 ∴S(mod 2)=1................B −−−−−− S=1009×2019 =(1009)(2000+16+3) =2000×1009+16×1009+3×1009 =2000×1009+16×1009+3000+27 =2000×1009+16×1009+3000+24+3 2000,16,3000 & 24 are divisible by 8 [Complete thousands are always divisible by8] ∴ S(mod 8)=3...............C From A,B &C S(mod 2)+S(mod 8)+S(mod 2018) =1+3+1009=1013](Q34353.png) | ||
| ||
Commented by Rasheed.Sindhi last updated on 09/May/18 | ||
 | ||