
Question and Answers Forum
Question Number 34186 by Joel578 last updated on 02/May/18
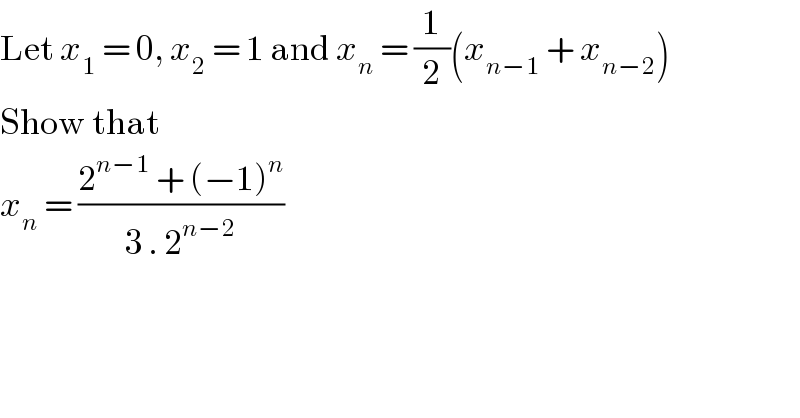
Commented by abdo mathsup 649 cc last updated on 02/May/18
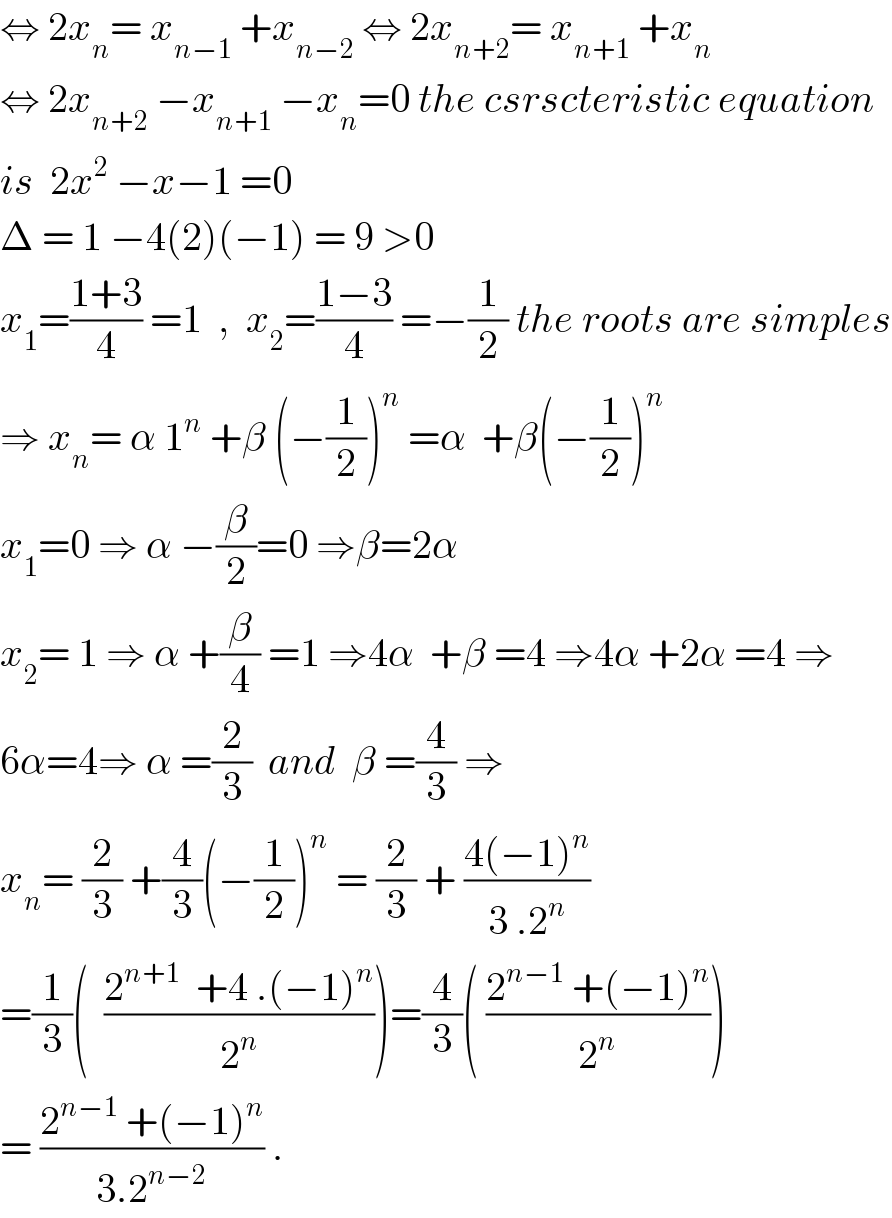
Answered by candre last updated on 02/May/18
![x_1 =((2^(1−1) +(−1)^1 )/(3∙2^(1−2) ))=((1−1)/(3/2))=0 x_2 =((2^(2−1) +(−1)^2 )/(3∙2^(2−2) ))=((2+1)/3)=1 x_(n−1) =((2^(n−2) +(−1)^(n−1) )/(3∙2^(n−3) )) x_(n−2) =((2^(n−3) +(−1)^(n−2) )/(3∙2^(n−4) )) ((x_(n−1) +x_(n−2) )/2)=(1/2)(((2^(n−2) +(−1)^(n−1) )/(3∙2^(n−3) ))+((2^(n−3) +(−1)^(n−2) )/(3∙2^(n−4) ))) =(1/(2^(n+1) ∙3))(((2^(n−2) −(−1)^n )/2^(−3) )+((2^(n−3) +(−1)^n )/2^(−4) )) =(1/(2^(n+1) ∙3))[2^3 (2^(n−2) −(−1)^n )+2^4 (2^(n−3) +(−1)^n )] =((2^3 2^(n−2) −2^3 (−1)^n +2^4 2^(n−3) +2^4 (−1)^n )/(2^(n+1) ∙3)) =((2^(n+2) +(2^4 −2^3 )(−1)^n )/(2^(n+1) ∙3)) =((2^3 (2^(n−1) +(2−1)(−1)^n ))/(2^(n+1) ∙3)) =((2^(n−1) +(−1)^n )/(2^(n−2) ∙3))](Q34188.png)
| ||
Question and Answers Forum | ||
Question Number 34186 by Joel578 last updated on 02/May/18 | ||
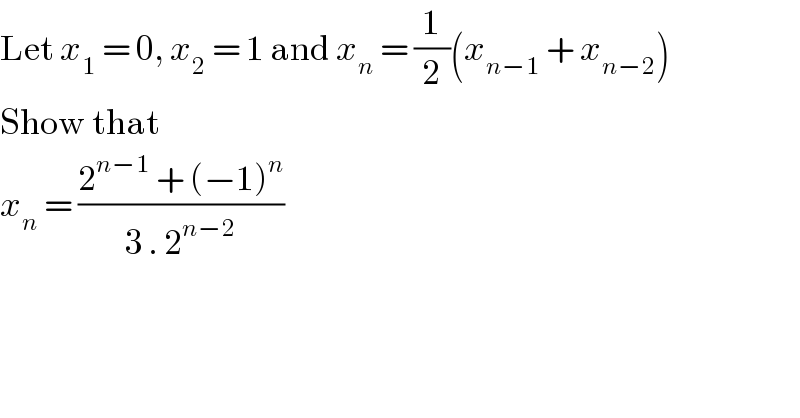 | ||
Commented by abdo mathsup 649 cc last updated on 02/May/18 | ||
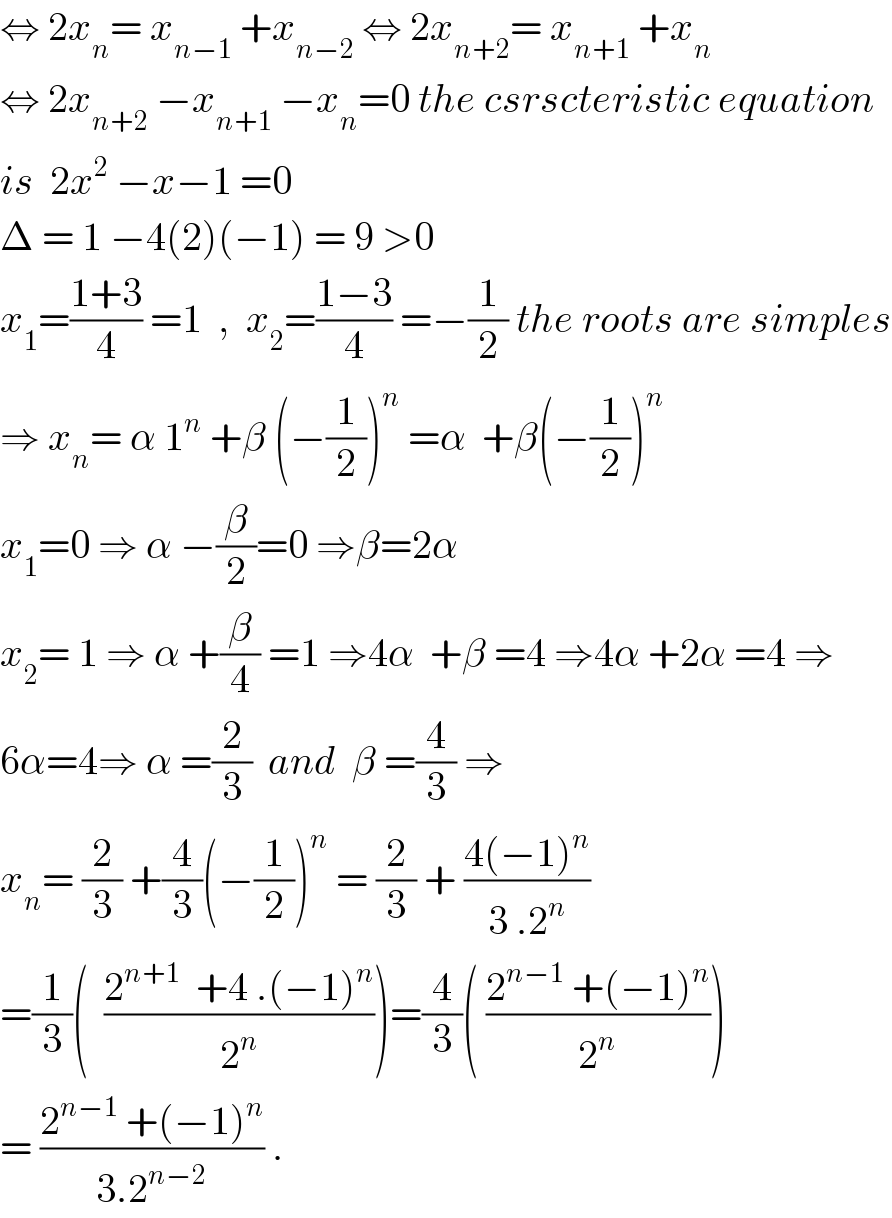 | ||
Answered by candre last updated on 02/May/18 | ||
![x_1 =((2^(1−1) +(−1)^1 )/(3∙2^(1−2) ))=((1−1)/(3/2))=0 x_2 =((2^(2−1) +(−1)^2 )/(3∙2^(2−2) ))=((2+1)/3)=1 x_(n−1) =((2^(n−2) +(−1)^(n−1) )/(3∙2^(n−3) )) x_(n−2) =((2^(n−3) +(−1)^(n−2) )/(3∙2^(n−4) )) ((x_(n−1) +x_(n−2) )/2)=(1/2)(((2^(n−2) +(−1)^(n−1) )/(3∙2^(n−3) ))+((2^(n−3) +(−1)^(n−2) )/(3∙2^(n−4) ))) =(1/(2^(n+1) ∙3))(((2^(n−2) −(−1)^n )/2^(−3) )+((2^(n−3) +(−1)^n )/2^(−4) )) =(1/(2^(n+1) ∙3))[2^3 (2^(n−2) −(−1)^n )+2^4 (2^(n−3) +(−1)^n )] =((2^3 2^(n−2) −2^3 (−1)^n +2^4 2^(n−3) +2^4 (−1)^n )/(2^(n+1) ∙3)) =((2^(n+2) +(2^4 −2^3 )(−1)^n )/(2^(n+1) ∙3)) =((2^3 (2^(n−1) +(2−1)(−1)^n ))/(2^(n+1) ∙3)) =((2^(n−1) +(−1)^n )/(2^(n−2) ∙3))](Q34188.png) | ||
| ||