
Question and Answers Forum
Previous in Relation and Functions Next in Relation and Functions
Question Number 34217 by abdo imad last updated on 02/May/18
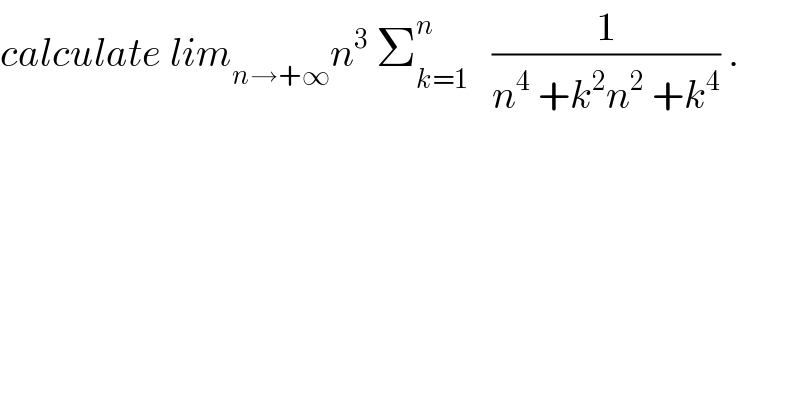
Commented by math khazana by abdo last updated on 04/May/18
![let put S_n = n^3 Σ_(k=1) ^n (1/(n^4 +k^2 n^2 +k^4 )) S_n = (1/n) Σ_(k=1) ^(n ) (1/(1+(k^2 /n^2 ) + (k^4 /n^4 ))) so S_n is a Rieman sum and lim_(n→+∞) S_n = ∫_0 ^1 (dx/(1+x^2 +x^4 )) x^4 +x^2 +1 = (x^2 +1)^2 −x^2 =(x^2 +1−x)(x^2 +1+x) let decompose F(x)= (1/((x^2 +x+1)(x^2 −x+1))) F(x) = ((ax+b)/(x^2 +x+1)) +((cx+d)/(x^2 −x+1)) F(−x) =F(x)⇒ ((−ax+b)/(x^2 −x+1)) +((−cx +d)/(x^2 +x+1)) =F(x) ⇒ c=−a and b=d ⇒ F(x) = ((ax+b)/(x^2 +x+1)) +((−ax +b)/(x^2 −x +1)) F(0) =1 = 2b ⇒ b=(1/2) ⇒ F(x)= (1/2)( ((2ax+1)/(x^2 +x+1)) +((−2ax +1)/(x^2 −x+1))) F(1) =(1/3) = (1/2)( ((2a+1)/3) +((−2a+1)/1))⇒ 1=(1/2)( 2a +1 −6a+3)=(1/2)(−4a+4)= −2a+2 ⇒ −2a=−1 ⇒ a =(1/2) ⇒ F(x) =(1/2)( ((x+1)/(x^2 +x+1)) −((x−1)/(x^2 −x +1))) ∫_0 ^1 (dx/(x^4 +x^2 +1)) =(1/4)∫_0 ^1 ((2x+2)/(x^2 +x +1))dx −(1/4)∫_0 ^1 ((2x−2)/(x^2 +x+1))dx ∫_0 ^1 ((2x+2)/(x^2 +x+1))dx =∫_0 ^1 ((2x+1)/(x^2 +x+1))dx +∫_0 ^1 (dx/(x^2 +x+1)) =[ln(x^2 +x+1)]_0 ^1 + ∫_0 ^1 (dx/((x+(1/2))^2 +(3/4))) (x+(1/2)=((√3)/2)u =ln(3) + ∫_(1/(√3)) ^(√3) (1/((3/4)( 1+u^2 ))) ((√3)/2)du =ln(3) +(4/3) ((√3)/2) ∫_(1/(√3)) ^(√3) (du/(1+u^2 )) =ln(3) +((2(√3))/3) (arctan((√3)) −arctan((1/(√3)))) ....](Q34337.png)
| ||
Question and Answers Forum | ||
Previous in Relation and Functions Next in Relation and Functions | ||
Question Number 34217 by abdo imad last updated on 02/May/18 | ||
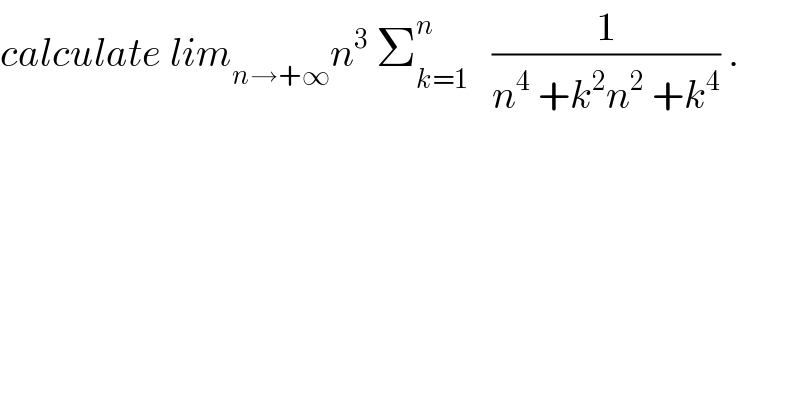 | ||
Commented by math khazana by abdo last updated on 04/May/18 | ||
![let put S_n = n^3 Σ_(k=1) ^n (1/(n^4 +k^2 n^2 +k^4 )) S_n = (1/n) Σ_(k=1) ^(n ) (1/(1+(k^2 /n^2 ) + (k^4 /n^4 ))) so S_n is a Rieman sum and lim_(n→+∞) S_n = ∫_0 ^1 (dx/(1+x^2 +x^4 )) x^4 +x^2 +1 = (x^2 +1)^2 −x^2 =(x^2 +1−x)(x^2 +1+x) let decompose F(x)= (1/((x^2 +x+1)(x^2 −x+1))) F(x) = ((ax+b)/(x^2 +x+1)) +((cx+d)/(x^2 −x+1)) F(−x) =F(x)⇒ ((−ax+b)/(x^2 −x+1)) +((−cx +d)/(x^2 +x+1)) =F(x) ⇒ c=−a and b=d ⇒ F(x) = ((ax+b)/(x^2 +x+1)) +((−ax +b)/(x^2 −x +1)) F(0) =1 = 2b ⇒ b=(1/2) ⇒ F(x)= (1/2)( ((2ax+1)/(x^2 +x+1)) +((−2ax +1)/(x^2 −x+1))) F(1) =(1/3) = (1/2)( ((2a+1)/3) +((−2a+1)/1))⇒ 1=(1/2)( 2a +1 −6a+3)=(1/2)(−4a+4)= −2a+2 ⇒ −2a=−1 ⇒ a =(1/2) ⇒ F(x) =(1/2)( ((x+1)/(x^2 +x+1)) −((x−1)/(x^2 −x +1))) ∫_0 ^1 (dx/(x^4 +x^2 +1)) =(1/4)∫_0 ^1 ((2x+2)/(x^2 +x +1))dx −(1/4)∫_0 ^1 ((2x−2)/(x^2 +x+1))dx ∫_0 ^1 ((2x+2)/(x^2 +x+1))dx =∫_0 ^1 ((2x+1)/(x^2 +x+1))dx +∫_0 ^1 (dx/(x^2 +x+1)) =[ln(x^2 +x+1)]_0 ^1 + ∫_0 ^1 (dx/((x+(1/2))^2 +(3/4))) (x+(1/2)=((√3)/2)u =ln(3) + ∫_(1/(√3)) ^(√3) (1/((3/4)( 1+u^2 ))) ((√3)/2)du =ln(3) +(4/3) ((√3)/2) ∫_(1/(√3)) ^(√3) (du/(1+u^2 )) =ln(3) +((2(√3))/3) (arctan((√3)) −arctan((1/(√3)))) ....](Q34337.png) | ||