
Question Number 34221 by abdo imad last updated on 03/May/18
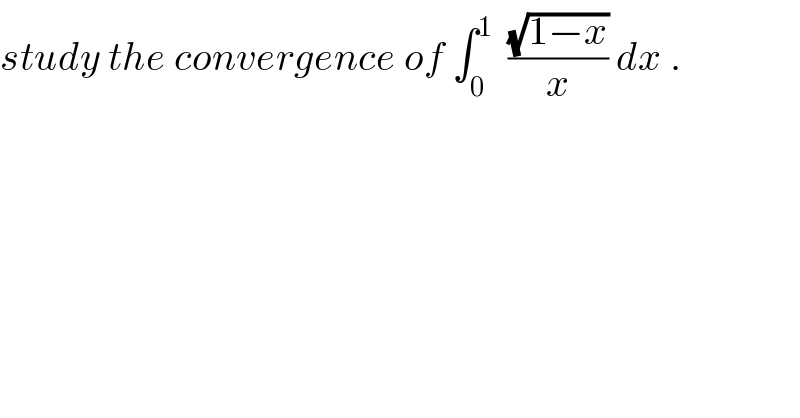
$${study}\:{the}\:{convergence}\:{of}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\sqrt{\mathrm{1}−{x}}}{{x}}\:{dx}\:. \\ $$
Commented by math khazana by abdo last updated on 04/May/18
![let put x= sin^2 θ ⇒ I = ∫_0 ^(π/2) ((cosθ)/(sin^2 θ)) .2sinθ cosθ dθ = ∫_0 ^(π/2) ((2cos^2 θ)/(sinθ)) dθ = 2 ∫_0 ^(π/2) ((1−sin^2 θ)/(sinθ))dθ = 2 ∫_0 ^(π/2) (dθ/(sinθ)) −2 ∫_0 ^(π/2) sinθ dθ but we have ∫_0 ^(π/2) sinθ dθ= [−cosθ]_0 ^(π/2) =1 and ch. tan((θ/2))=x give ∫_ξ ^(π/2) (dθ/(sinθ)) = ∫_ξ ^(π/4) (1/((2x)/(1+x^2 ))) ((2dx)/(1+x^2 )) = ∫_ξ ^(π/4) (dx/x) =ln((π/4)) −lnξ so lim_(ξ→0^+ ) ∫_ξ ^(π/4) (dθ/(sinθ)) = +∞ ⇒ I is divergent.](Q34323.png)
$${let}\:{put}\:{x}=\:{sin}^{\mathrm{2}} \theta\:\:\Rightarrow\:{I}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{cos}\theta}{{sin}^{\mathrm{2}} \theta}\:.\mathrm{2}{sin}\theta\:{cos}\theta\:{d}\theta \\ $$$$=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{\mathrm{2}{cos}^{\mathrm{2}} \theta}{{sin}\theta}\:{d}\theta\:=\:\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{1}−{sin}^{\mathrm{2}} \theta}{{sin}\theta}{d}\theta \\ $$$$=\:\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{d}\theta}{{sin}\theta}\:\:−\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{sin}\theta\:{d}\theta\:\:{but}\:{we}\:{have} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{sin}\theta\:{d}\theta=\:\left[−{cos}\theta\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} =\mathrm{1}\:\:{and}\:{ch}.\:{tan}\left(\frac{\theta}{\mathrm{2}}\right)={x}\:{give} \\ $$$$\:\int_{\xi} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{d}\theta}{{sin}\theta}\:=\:\int_{\xi} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\frac{\mathrm{1}}{\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }}\:\frac{\mathrm{2}{dx}}{\mathrm{1}+{x}^{\mathrm{2}} }\:=\:\int_{\xi} ^{\frac{\pi}{\mathrm{4}}} \:\:\frac{{dx}}{{x}} \\ $$$$={ln}\left(\frac{\pi}{\mathrm{4}}\right)\:−{ln}\xi\:\:\:{so}\:{lim}_{\xi\rightarrow\mathrm{0}^{+} } \:\:\:\int_{\xi} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\frac{{d}\theta}{{sin}\theta}\:=\:+\infty \\ $$$$\Rightarrow\:{I}\:{is}\:{divergent}. \\ $$
Answered by Joel578 last updated on 03/May/18
![I = lim_(t→0^+ ) (∫_t ^1 ((√(1 − x))/x) dx) ∫_t ^1 ((√(1 − x))/x) dx (u = (√(1− x)) → du = −(1/(2u)) dx) = −∫_(√(1−t)) ^0 ((2u^2 )/(1 − u^2 )) du = 2∫_(√(1−t)) ^0 (u^2 /(u^2 − 1)) du = 2 ∫_(√(1−t)) ^0 (1 + (1/(u^2 − 1))) du = 2 ∫_(√(1−t)) ^0 (1 + (1/(2(u − 1))) − (1/(2(u + 1)))) du = 2 [u + (1/2) ln (((u − 1)/(u + 1)))]_(√(1−t)) ^0 = 2[0 + (1/2) ln (−1) − (√(1−t)) − (1/2) ln ((((√(1−t)) − 1)/((√(1−t)) + 1)))] = iπ − 2(√(1−t)) − ln ((((√(1−t)) − 1)/((√(1−t)) + 1))) I = lim_(t→0^+ ) [iπ − 2(√(1−t)) − ln ((((√(1−t)) − 1)/((√(1−t)) + 1)))] = iπ − 2 − ln 0 = ∞ The integral doesnt converge](Q34252.png)
$${I}\:=\:\underset{{t}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\left(\int_{{t}} ^{\mathrm{1}} \:\frac{\sqrt{\mathrm{1}\:−\:{x}}}{{x}}\:{dx}\right) \\ $$$$ \\ $$$$\int_{{t}} ^{\mathrm{1}} \:\frac{\sqrt{\mathrm{1}\:−\:{x}}}{{x}}\:{dx}\:\:\left({u}\:=\:\sqrt{\mathrm{1}−\:{x}}\:\:\rightarrow\:\:{du}\:=\:−\frac{\mathrm{1}}{\mathrm{2}{u}}\:{dx}\right) \\ $$$$=\:−\int_{\sqrt{\mathrm{1}−{t}}} ^{\mathrm{0}} \:\frac{\mathrm{2}{u}^{\mathrm{2}} }{\mathrm{1}\:−\:{u}^{\mathrm{2}} }\:{du}\:=\:\mathrm{2}\int_{\sqrt{\mathrm{1}−{t}}} ^{\mathrm{0}} \:\frac{{u}^{\mathrm{2}} }{{u}^{\mathrm{2}} \:−\:\mathrm{1}}\:{du} \\ $$$$=\:\mathrm{2}\:\int_{\sqrt{\mathrm{1}−{t}}} ^{\mathrm{0}} \:\:\left(\mathrm{1}\:+\:\frac{\mathrm{1}}{{u}^{\mathrm{2}} \:−\:\mathrm{1}}\right)\:{du} \\ $$$$=\:\mathrm{2}\:\int_{\sqrt{\mathrm{1}−{t}}} ^{\mathrm{0}} \:\left(\mathrm{1}\:+\:\frac{\mathrm{1}}{\mathrm{2}\left({u}\:−\:\mathrm{1}\right)}\:−\:\frac{\mathrm{1}}{\mathrm{2}\left({u}\:+\:\mathrm{1}\right)}\right)\:{du} \\ $$$$=\:\mathrm{2}\:\left[{u}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{ln}\:\left(\frac{{u}\:−\:\mathrm{1}}{{u}\:+\:\mathrm{1}}\right)\right]_{\sqrt{\mathrm{1}−{t}}} ^{\mathrm{0}} \\ $$$$=\:\mathrm{2}\left[\mathrm{0}\:\:+\:\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{ln}\:\left(−\mathrm{1}\right)\:−\:\sqrt{\mathrm{1}−{t}}\:−\:\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{ln}\:\left(\frac{\sqrt{\mathrm{1}−{t}}\:−\:\mathrm{1}}{\sqrt{\mathrm{1}−{t}}\:+\:\mathrm{1}}\right)\right] \\ $$$$=\:{i}\pi\:−\:\mathrm{2}\sqrt{\mathrm{1}−{t}}\:−\:\mathrm{ln}\:\left(\frac{\sqrt{\mathrm{1}−{t}}\:−\:\mathrm{1}}{\sqrt{\mathrm{1}−{t}}\:+\:\mathrm{1}}\right) \\ $$$$ \\ $$$${I}\:=\:\underset{{t}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\:\left[{i}\pi\:−\:\mathrm{2}\sqrt{\mathrm{1}−{t}}\:−\:\mathrm{ln}\:\left(\frac{\sqrt{\mathrm{1}−{t}}\:−\:\mathrm{1}}{\sqrt{\mathrm{1}−{t}}\:+\:\mathrm{1}}\right)\right] \\ $$$$\:\:\:\:=\:{i}\pi\:−\:\mathrm{2}\:−\:\mathrm{ln}\:\mathrm{0} \\ $$$$\:\:\:\:=\:\infty \\ $$$$\mathrm{The}\:\mathrm{integral}\:\mathrm{doesnt}\:\mathrm{converge} \\ $$
Commented by math khazana by abdo last updated on 04/May/18
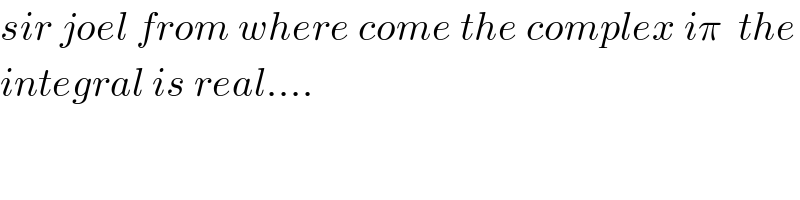
$${sir}\:{joel}\:{from}\:{where}\:{come}\:{the}\:{complex}\:{i}\pi\:\:{the} \\ $$$${integral}\:{is}\:{real}.... \\ $$
