calculate ∫_0 ^1 arctan(x^2 )dx


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 34227 by abdo imad last updated on 03/May/18

$c a l c u l a t e \int_{0}^{1} a r c t a n (x^{2}) d x$
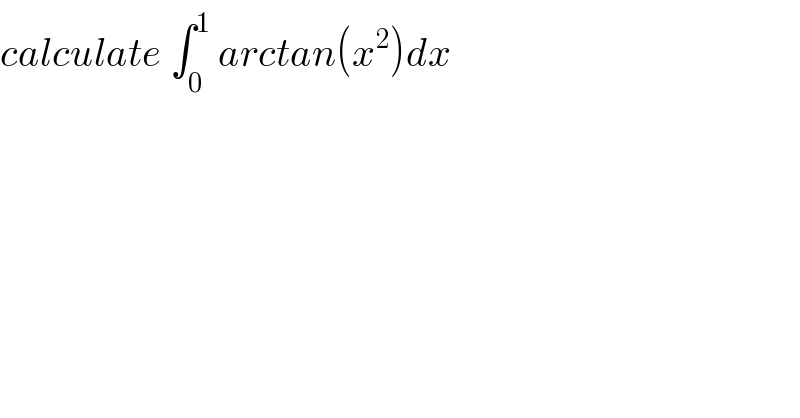
Commented by math khazana by abdo last updated on 04/May/18

$l e t p u t I = \int_{0}^{1} a r c t a n (x^{2}) d x b y p a r t s u^{^{'}} = 1 a n d$ $v = a r c t a n (x^{2}) \Rightarrow I = {[x a r c t a n (x^{2})]}_{0}^{1} - \int_{0}^{1} x \frac{2 x}{1 + x^{4}} d x$ $= \frac{π}{4} - 2 \int_{0}^{1} \frac{x^{2}}{1 + x^{4}} d x l e t d e c o m p o s e$ $F (x) = \frac{x^{2}}{1 + x^{4}} = \frac{x^{2}}{{(x^{2} + 1)}^{2} - 2 x^{2}} = \frac{x^{2}}{(x^{2} - \sqrt{2} x + 1) (x^{2} + \sqrt{2} x + 1)}$ $F (x) = \frac{a x + b}{x^{2} - \sqrt{2} x + 1} + \frac{c x + d}{x^{2} + \sqrt{2} x + 1}$ $F (- x) = F (x) \Rightarrow c = - a a n d d = b \Rightarrow$ $F (x) = \frac{a x + b}{x^{2} - \sqrt{2} x + 1} + \frac{- a x + b}{x^{2} + \sqrt{2} x + 1}$ $F (0) = 0 = 2 b \Rightarrow b = 0 \Rightarrow$ $F (x) = \frac{a x}{x^{2} - \sqrt{2} x + 1} - \frac{a x}{x^{2} + \sqrt{2} x + 1}$ $F (1) = \frac{1}{2} = \frac{a}{2 - \sqrt{2}} - \frac{a}{2 + \sqrt{2}} = (\frac{2 + \sqrt{2} - 2 + \sqrt{2}}{2}) a$ $= \sqrt{2} a \Rightarrow a = \frac{1}{2 \sqrt{2}} \Rightarrow$ $F (x) = \frac{1}{2 \sqrt{2}} (\frac{x}{x^{2} - \sqrt{2} x + 1} - \frac{x}{x^{2} + \sqrt{2} x + 1})$ $\int_{0}^{1} \frac{x^{2}}{1 + x^{4}} d x = \frac{1}{2 \sqrt{2}} \int_{0}^{1} \frac{x}{x^{2} - \sqrt{2} x + 1} d x - \frac{1}{2 \sqrt{2}} \int_{0}^{1} \frac{x}{x^{2} + \sqrt{2} x + 1} d x$
Commented by math khazana by abdo last updated on 04/May/18

$\int_{0}^{1} \frac{x}{x^{2} - \sqrt{2} x + 1} d x = \frac{1}{2} \int_{0}^{1} \frac{2 x - \sqrt{2} + \sqrt{2}}{x^{2} - \sqrt{2} x + 1} d x$ $= \frac{1}{2} {[l n (x^{2} - \sqrt{2} x + 1)]}_{0}^{1} + \frac{\sqrt{2}}{2} \int_{0}^{1} \frac{d x}{x^{2} - \sqrt{2} x + 1}$ $= \frac{1}{2} l n (2 - \sqrt{2}) + \frac{\sqrt{2}}{2} \int_{0}^{1} \frac{d x}{x^{2} - \sqrt{2} x + 1} b u t$ $\int_{0}^{1} \frac{d x}{x^{2} - \sqrt{2} x + 1} = \int_{0}^{1} \frac{d x}{x^{2} - 2 \frac{\sqrt{2}}{2} x + \frac{1}{4} + \frac{3}{4}}$ $= \int_{0}^{1} \frac{d x}{{(x - \frac{\sqrt{2}}{2})}^{2} + \frac{3}{4}} =_{x - \frac{\sqrt{2}}{2} = \frac{\sqrt{3}}{2} t} \int_{- \frac{\sqrt{2}}{\sqrt{3}}}^{\frac{2}{\sqrt{3}} (1 - \frac{\sqrt{2}}{2})} \frac{\frac{\sqrt{3}}{2} d t}{\frac{3}{4} (1 + t^{2})}$ $= \frac{4}{3} \frac{\sqrt{3}}{2} \int_{- \frac{\sqrt{2}}{\sqrt{3}}}^{\frac{2}{\sqrt{3}} - \frac{\sqrt{2}}{\sqrt{3}}} \frac{d t}{1 + t^{2}} = \frac{2 \sqrt{3}}{3} (a r c t a n (\frac{2}{\sqrt{3}} - \frac{\sqrt{2}}{\sqrt{3}}) + a r c t a n (\frac{\sqrt{2}}{\sqrt{3}})) \Rightarrow$ $\int_{0}^{1} \frac{x}{x^{2} - \sqrt{2} x + 1} d x = \frac{1}{2} l n (2 - \sqrt{2})$ $+ \frac{2 \sqrt{3}}{3} (a r c t a n (\frac{2}{\sqrt{3}} - \frac{\sqrt{2}}{\sqrt{3}}) + a r c t a n (\frac{\sqrt{2}}{\sqrt{3}}))$ $\int_{0}^{1} \frac{x}{x^{2} + \sqrt{2} x + 1} d x =_{x = - t} \int_{0}^{- 1} \frac{t d t}{t^{2} - \sqrt{2} t + 1}$ $a n d t h i s c a c u l a t e d a b o v e . . . .$
	Answered by tanmay.chaudhury50@gmail.com last updated on 03/May/18

	$l e t I = \int {t a n}^{- 1} (x^{2}) d x$ $= {t a n}^{- 1} (x^{2}) \int d x - \int [\frac{d}{d x} {t a n}^{- 1} x^{2 .} . \int d x] d x$ $= {x t a n}^{- 1} (x^{2}) - \int \frac{2 x}{1 + x^{4}} . x d x$ $= {x t a n}^{- 1} x - 2 \int \frac{x^{2}}{1 + x^{4}} d x$ $i h a v e a l r e d y s o l v e d \int \frac{x^{2}}{1 + x^{4}} d x$ $p l s c o - r e l a t e$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum