
Question and Answers Forum
Question Number 34312 by prof Abdo imad last updated on 03/May/18
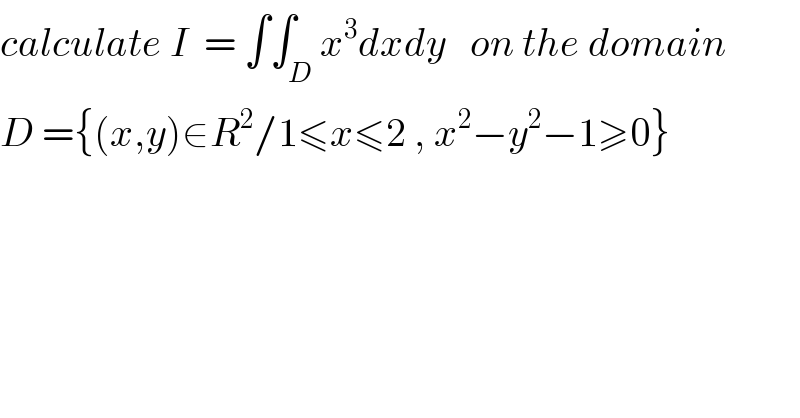
Commented by math khazana by abdo last updated on 05/May/18
![x^2 −y^2 −1≥0 ⇒ x^2 −1 ≥y^2 ⇒y^2 ≤ x^2 −1 ⇒ −(√(x^2 −1)) ≤y≤(√(x^2 −1)) I = ∫_1 ^2 ( ∫_(−(√(x^2 −1))) ^(√(x^2 −1)) dy)x^3 dx = 2 ∫_1 ^2 x^3 (√(x^2 −1))dx changement x=ch(t) ⇔ t argchx =ln( x +(√(x^2 −1))) I = 2 ∫_0 ^(ln(2+(√3))) ch^3 t sh(t)sh(t)dt by parts u=sht and v^′ =sht ch^3 t I =2( [(1/4)sht ch^4 t]_0 ^(ln(2+(√3))) −∫_0 ^(ln(2+(√3))) cht (1/4)ch^4 dt) I =(1/2)( sh(ln(2+(√3)))ch^4 (ln(2+(√3)) −(1/2) ∫_0 ^(ln(2+(√3))) ch^5 t dt but ch^5 t = (((e^t +e^(−t) )/2))^5 =(1/(32)) Σ_(k=0) ^5 C_5 ^k e^(kt) e^((5−k)t) ...](Q34417.png)
| ||
Question and Answers Forum | ||
Question Number 34312 by prof Abdo imad last updated on 03/May/18 | ||
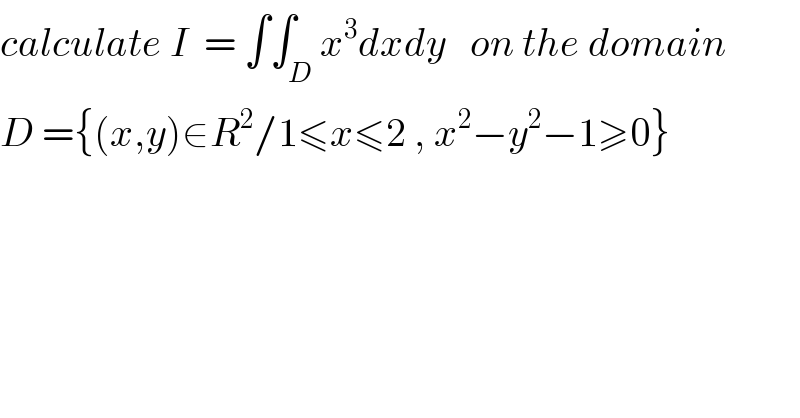 | ||
Commented by math khazana by abdo last updated on 05/May/18 | ||
![x^2 −y^2 −1≥0 ⇒ x^2 −1 ≥y^2 ⇒y^2 ≤ x^2 −1 ⇒ −(√(x^2 −1)) ≤y≤(√(x^2 −1)) I = ∫_1 ^2 ( ∫_(−(√(x^2 −1))) ^(√(x^2 −1)) dy)x^3 dx = 2 ∫_1 ^2 x^3 (√(x^2 −1))dx changement x=ch(t) ⇔ t argchx =ln( x +(√(x^2 −1))) I = 2 ∫_0 ^(ln(2+(√3))) ch^3 t sh(t)sh(t)dt by parts u=sht and v^′ =sht ch^3 t I =2( [(1/4)sht ch^4 t]_0 ^(ln(2+(√3))) −∫_0 ^(ln(2+(√3))) cht (1/4)ch^4 dt) I =(1/2)( sh(ln(2+(√3)))ch^4 (ln(2+(√3)) −(1/2) ∫_0 ^(ln(2+(√3))) ch^5 t dt but ch^5 t = (((e^t +e^(−t) )/2))^5 =(1/(32)) Σ_(k=0) ^5 C_5 ^k e^(kt) e^((5−k)t) ...](Q34417.png) | ||