
Question and Answers Forum
Question Number 34315 by prof Abdo imad last updated on 03/May/18
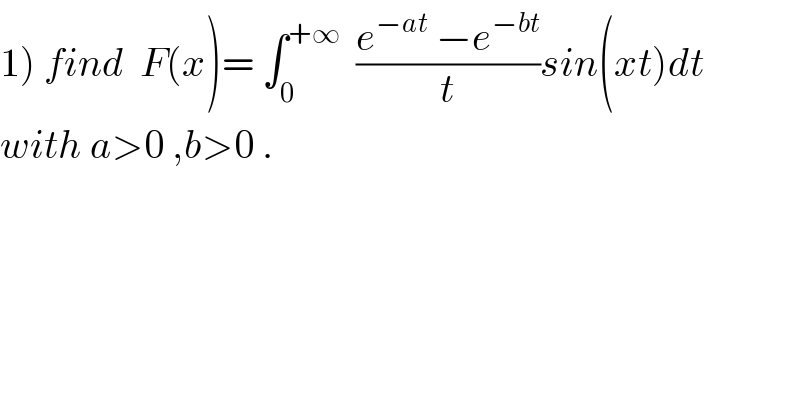
Commented bymath khazana by abdo last updated on 05/May/18
![we have F^′ (x) = ∫_0 ^∞ (e^(−at) −e^(−bt) ) cos(xt)dt =Re( ∫_0 ^∞ (e^(−at) −e^(−bt) )e^(ixt) dt) =Re( ∫_0 ^∞ (e^((−a +ix)t) −e^((−b +ix)t) )dt but ∫_0 ^∞ e^((−a+ix)t) dt = [ (1/(−a +ix)) e^((−1+ix)t) ]_0 ^(+∞) = (1/(−a +ix)) =((−1)/(a−ix)) =−((a+ix)/(a^2 +x^2 )) by the same manner ∫_0 ^∞ e^((−b+ix)t) dt = −((b +ix)/(b^2 +x^2 )) ⇒ F^′ (x) = Re( ((b+ix)/(b^2 +x^2 )) −((a+ix)/(a^2 +x^2 ))) =(b/(b^2 +x^2 )) − (a/(a^2 +x^2 )) ⇒ F(x)= ∫_0 ^x (b/(b^2 +t^2 ))dt −∫_0 ^x (a/(a^2 +t^2 ))dt +λ but ∫_0 ^x (b/(b^2 +t^2 ))dt =_(t=bu) ∫_0 ^(x/b) (b/(b^2 (1+u^2 ))) bdu = arctan((x/b)) ⇒F(x)= arctan((x/b)) −arctan((x/a)) +λ λ =F(0) ⇒F(x)=arctan((x/b)) −arctan((x/a)) .](Q34415.png)
Commented bymath khazana by abdo last updated on 08/May/18

| ||
Question and Answers Forum | ||
Question Number 34315 by prof Abdo imad last updated on 03/May/18 | ||
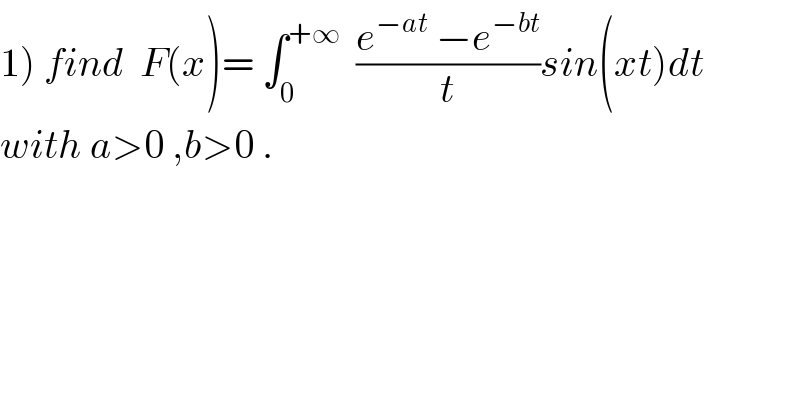 | ||
Commented bymath khazana by abdo last updated on 05/May/18 | ||
![we have F^′ (x) = ∫_0 ^∞ (e^(−at) −e^(−bt) ) cos(xt)dt =Re( ∫_0 ^∞ (e^(−at) −e^(−bt) )e^(ixt) dt) =Re( ∫_0 ^∞ (e^((−a +ix)t) −e^((−b +ix)t) )dt but ∫_0 ^∞ e^((−a+ix)t) dt = [ (1/(−a +ix)) e^((−1+ix)t) ]_0 ^(+∞) = (1/(−a +ix)) =((−1)/(a−ix)) =−((a+ix)/(a^2 +x^2 )) by the same manner ∫_0 ^∞ e^((−b+ix)t) dt = −((b +ix)/(b^2 +x^2 )) ⇒ F^′ (x) = Re( ((b+ix)/(b^2 +x^2 )) −((a+ix)/(a^2 +x^2 ))) =(b/(b^2 +x^2 )) − (a/(a^2 +x^2 )) ⇒ F(x)= ∫_0 ^x (b/(b^2 +t^2 ))dt −∫_0 ^x (a/(a^2 +t^2 ))dt +λ but ∫_0 ^x (b/(b^2 +t^2 ))dt =_(t=bu) ∫_0 ^(x/b) (b/(b^2 (1+u^2 ))) bdu = arctan((x/b)) ⇒F(x)= arctan((x/b)) −arctan((x/a)) +λ λ =F(0) ⇒F(x)=arctan((x/b)) −arctan((x/a)) .](Q34415.png) | ||
Commented bymath khazana by abdo last updated on 08/May/18 | ||
 | ||