lim_(x→1) {1−x+[x−1]+[1−x]} = ? [.]= greatest integer function.


Question and Answers Forum

All Questions Topic List
Limits Questions
Previous in All Question Next in All Question
Previous in Limits Next in Limits
Question Number 34374 by rahul 19 last updated on 05/May/18
$lim_(x→1) {1−x+[x−1]+[1−x]} = ? [.]= greatest integer function.$
${l i m}_{x \to 1} {1 - x + [x - 1] + [1 - x]} = ?$ $[.] = g r e a t e s t i n t e g e r f u n c t i o n .$
	Answered by MJS last updated on 05/May/18
	$[x−1]=[x]−1 [1−x]=[−x]+1 1−x+[x−1]+[1−x]=1−x+[x]+[−x] [x]+[−x]= { ((0; x∈Z)),((−1; x∈R\Z)) :} f(x)=1−x+[x]+[−x] f(1)=0 but lim_(x→1) f(x)=−1 the graph of f(x) is the straight line y=−x except for x∈Z where it′s y=1−x$
	$[x - 1] = [x] - 1$ $[1 - x] = [- x] + 1$ $1 - x + [x - 1] + [1 - x] = 1 - x + [x] + [- x]$ $[x] + [- x] = {\begin{cases} 0; x \in Z \\ - 1; x \in R ∖ Z \end{cases}$ $f (x) = 1 - x + [x] + [- x]$ $f (1) = 0$ $but$ $\lim_{x \to 1} f (x) = - 1$ $the graph of f (x) is the straight line y = - x$ $except for x \in Z where {it}^{'} s y = 1 - x$
	Commented by MJS last updated on 05/May/18

	$yes . in this case the limit from both sides is$ $- 1 although {that}^{'} s not the value of the$ $function at this point .$
	Commented by rahul 19 last updated on 05/May/18

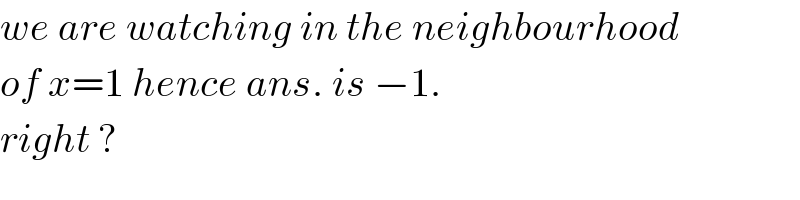
	$w e a r e w a t c h i n g i n t h e n e i g h b o u r h o o d$ $o f x = 1 h e n c e a n s . i s - 1 .$ $r i g h t ?$
	Commented by rahul 19 last updated on 05/May/18

	$T h a n k y o u s i r .$
	Commented by rahul 19 last updated on 05/May/18

	$e x a c t l y!$
	Answered by math khazana by abdo last updated on 05/May/18

	$l e t p u t x - 1 = t {l i m}_{x \to 1} 1 - x + [x - 1] + [1 - x]$ $= {l i m}_{t \to 0} - t + [t] + [- t] l e t p u t f (t) = - t + [t] + [- t]$ $w e h a v e f (0) = 0 b u t$ ${l i m}_{t \to 0^{+}} f (t) = - 1 a n d {l i m}_{t \to 0^{-}} f (t) = - 1 s o$ $l i m i t s e x i s t a t l e f t a n d r i g h t b u t f i s n o t c o n t i n u e$ $a t 0 .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum