Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 34458 by rahul 19 last updated on 06/May/18

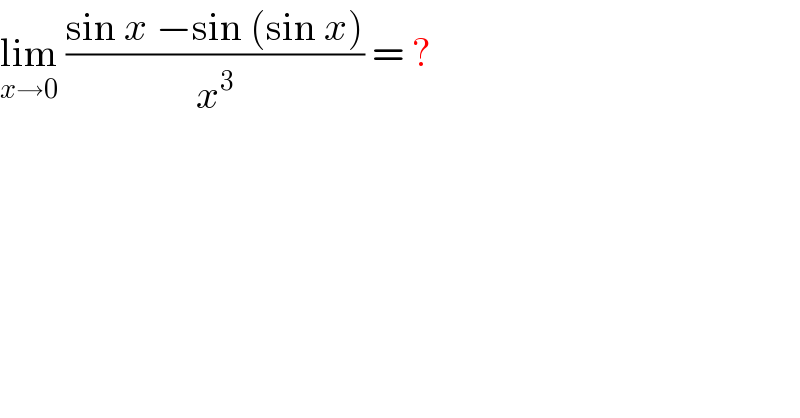
lim_(x→0) ((sin x −sin (sin x))/x^3 ) = ?

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:{x}\:−\mathrm{sin}\:\left(\mathrm{sin}\:{x}\right)}{{x}^{\mathrm{3}} }\:=\:? \\ $$

Commented by math khazana by abdo last updated on 06/May/18

we have sinx = x −(x^3 /(3!)) + 0(x^5 ) (x→0) and sin(sinx) =sin(x −(x^3 /(3!)) +0(x^5 )) =x −(x^3 /(3!)) − (x−(x^3 /(3!)))^3 ×(1/(3!)) +0 ( x^9 ) ⇒ sinx −sin(sinx) = (1/(3!))( x^3 −3x^2 (x^3 /(3!)) +....) +0(x^9 ) ⇒ lim_(x→0) ((sinx −sin(sinx))/x^3 ) = (1/(3!)) =(1/6) .

$${we}\:{have}\:{sinx}\:=\:{x}\:−\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}\:+\:\mathrm{0}\left({x}^{\mathrm{5}} \right)\:\:\left({x}\rightarrow\mathrm{0}\right)\:{and} \\ $$$${sin}\left({sinx}\right)\:={sin}\left({x}\:−\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}\:+\mathrm{0}\left({x}^{\mathrm{5}} \right)\right) \\ $$$$={x}\:−\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}\:−\:\left({x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}\right)^{\mathrm{3}} ×\frac{\mathrm{1}}{\mathrm{3}!}\:\:+\mathrm{0}\:\left(\:{x}^{\mathrm{9}} \right)\:\Rightarrow \\ $$$${sinx}\:−{sin}\left({sinx}\right)\:=\:\frac{\mathrm{1}}{\mathrm{3}!}\left(\:{x}^{\mathrm{3}} \:−\mathrm{3}{x}^{\mathrm{2}} \:\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}\:+....\right)\:+\mathrm{0}\left({x}^{\mathrm{9}} \right)\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \:\frac{{sinx}\:−{sin}\left({sinx}\right)}{{x}^{\mathrm{3}} }\:=\:\frac{\mathrm{1}}{\mathrm{3}!}\:=\frac{\mathrm{1}}{\mathrm{6}}\:. \\ $$

Commented by math khazana by abdo last updated on 06/May/18

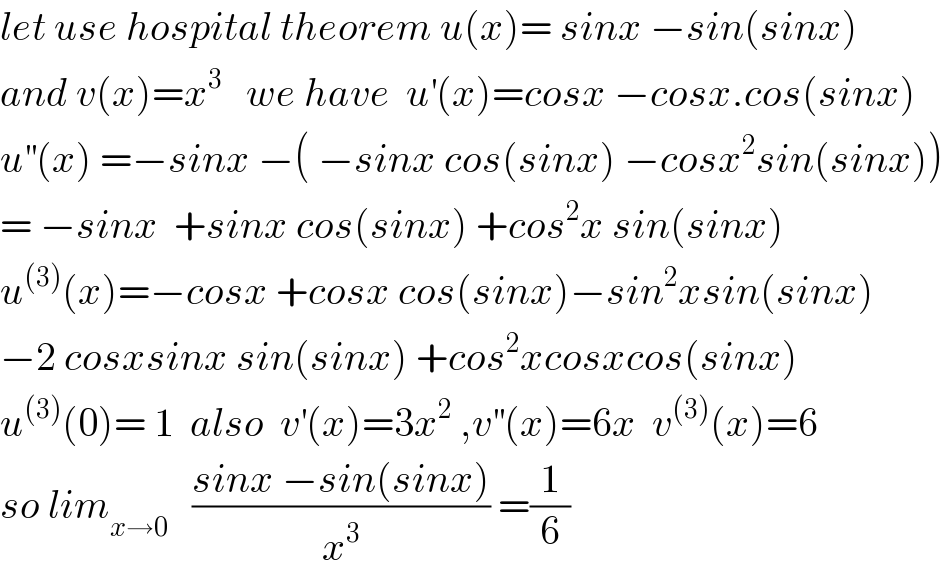
let use hospital theorem u(x)= sinx −sin(sinx) and v(x)=x^3 we have u^′ (x)=cosx −cosx.cos(sinx) u^(′′) (x) =−sinx −( −sinx cos(sinx) −cosx^2 sin(sinx)) = −sinx +sinx cos(sinx) +cos^2 x sin(sinx) u^((3)) (x)=−cosx +cosx cos(sinx)−sin^2 xsin(sinx) −2 cosxsinx sin(sinx) +cos^2 xcosxcos(sinx) u^((3)) (0)= 1 also v^′ (x)=3x^2 ,v^(′′) (x)=6x v^((3)) (x)=6 so lim_(x→0) ((sinx −sin(sinx))/x^3 ) =(1/6)

$${let}\:{use}\:{hospital}\:{theorem}\:{u}\left({x}\right)=\:{sinx}\:−{sin}\left({sinx}\right) \\ $$$${and}\:{v}\left({x}\right)={x}^{\mathrm{3}} \:\:\:{we}\:{have}\:\:{u}^{'} \left({x}\right)={cosx}\:−{cosx}.{cos}\left({sinx}\right) \\ $$$${u}^{''} \left({x}\right)\:=−{sinx}\:−\left(\:−{sinx}\:{cos}\left({sinx}\right)\:−{cosx}^{\mathrm{2}} {sin}\left({sinx}\right)\right) \\ $$$$=\:−{sinx}\:\:+{sinx}\:{cos}\left({sinx}\right)\:+{cos}^{\mathrm{2}} {x}\:{sin}\left({sinx}\right) \\ $$$${u}^{\left(\mathrm{3}\right)} \left({x}\right)=−{cosx}\:+{cosx}\:{cos}\left({sinx}\right)−{sin}^{\mathrm{2}} {xsin}\left({sinx}\right) \\ $$$$−\mathrm{2}\:{cosxsinx}\:{sin}\left({sinx}\right)\:+{cos}^{\mathrm{2}} {xcosxcos}\left({sinx}\right) \\ $$$${u}^{\left(\mathrm{3}\right)} \left(\mathrm{0}\right)=\:\mathrm{1}\:\:{also}\:\:{v}^{'} \left({x}\right)=\mathrm{3}{x}^{\mathrm{2}} \:,{v}^{''} \left({x}\right)=\mathrm{6}{x}\:\:{v}^{\left(\mathrm{3}\right)} \left({x}\right)=\mathrm{6} \\ $$$${so}\:{lim}_{{x}\rightarrow\mathrm{0}} \:\:\:\frac{{sinx}\:−{sin}\left({sinx}\right)}{{x}^{\mathrm{3}} }\:=\frac{\mathrm{1}}{\mathrm{6}} \\ $$

Commented by math khazana by abdo last updated on 06/May/18

due to hospital theorem my answer is correct.

$${due}\:{to}\:{hospital}\:{theorem}\:{my}\:{answer}\:{is}\:{correct}. \\ $$

Commented by rahul 19 last updated on 07/May/18

Thank you sir !

Answered by tanmay.chaudhury50@gmail.com last updated on 06/May/18

=((lim )/(x→0)){2cos(((x+sinx)/2)).sin(((x−sinx)/2))}/x^3 =((lim)/(x→0))2.cos0.sin(((x−sinx)/2))/x^3 sinx=(x/1)−(x^3 /(3!))+(x^5 /(5!))−... =((lim)/(x→0))2.sin((x^3 /(3!)))/x^3 =((lim)/(x→0))((2sin((x^3 /(3!))))/((x^3 /(3!))×3!)) =(2/(3!^ )) =2/6=1/3

$$=\frac{{lim}\:}{{x}\rightarrow\mathrm{0}}\left\{\mathrm{2}{cos}\left(\frac{{x}+{sinx}}{\mathrm{2}}\right).{sin}\left(\frac{{x}−{sinx}}{\mathrm{2}}\right)\right\}/{x}^{\mathrm{3}} \\ $$$$=\frac{{lim}}{{x}\rightarrow\mathrm{0}}\mathrm{2}.{cos}\mathrm{0}.{sin}\left(\frac{{x}−{sinx}}{\mathrm{2}}\right)/{x}^{\mathrm{3}} \\ $$$${sinx}=\frac{{x}}{\mathrm{1}}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}+\frac{{x}^{\mathrm{5}} }{\mathrm{5}!}−... \\ $$$$=\frac{{lim}}{{x}\rightarrow\mathrm{0}}\mathrm{2}.{sin}\left(\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}\right)/{x}^{\mathrm{3}} \\ $$$$=\frac{{lim}}{{x}\rightarrow\mathrm{0}}\frac{\mathrm{2}{sin}\left(\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}\right)}{\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}×\mathrm{3}!} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}\overset{} {!}} \\ $$$$=\mathrm{2}/\mathrm{6}=\mathrm{1}/\mathrm{3} \\ $$

Commented by MJS last updated on 06/May/18

something went wrong...

$$\mathrm{something}\:\mathrm{went}\:\mathrm{wrong}... \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 07/May/18

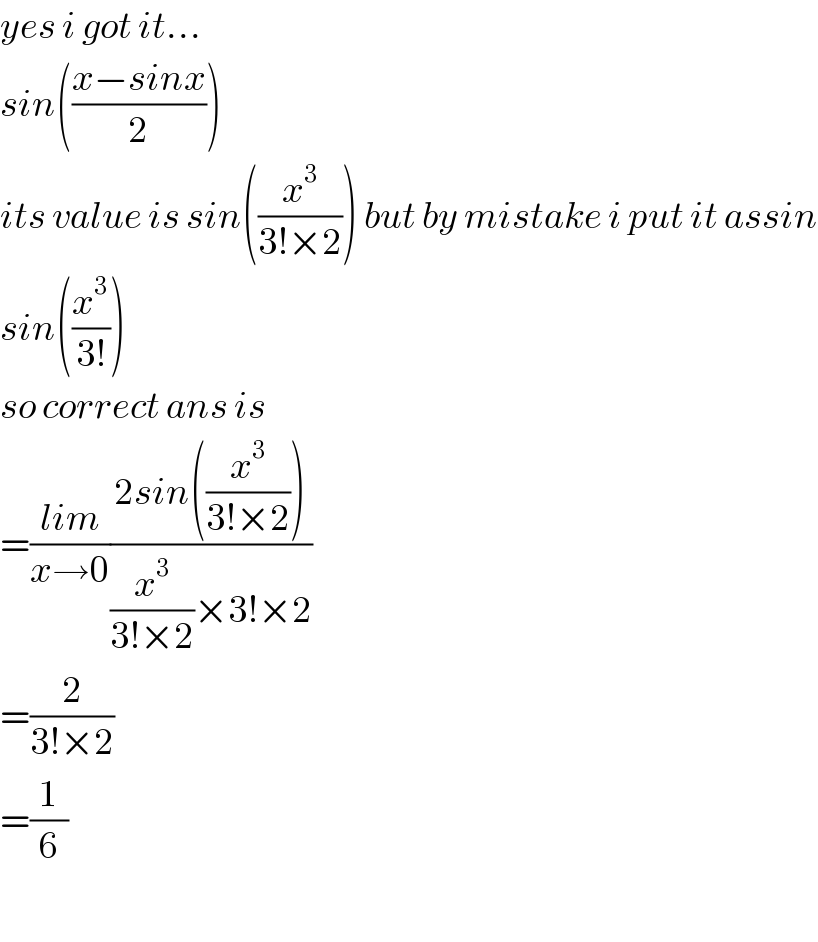
yes i got it... sin(((x−sinx)/2)) its value is sin((x^3 /(3!×2))) but by mistake i put it assin sin((x^3 /(3!))) so correct ans is =((lim)/(x→0))((2sin((x^3 /(3!×2))))/((x^3 /(3!×2))×3!×2)) =(2/(3!×2)) =(1/6)

$${yes}\:{i}\:{got}\:{it}... \\ $$$${sin}\left(\frac{{x}−{sinx}}{\mathrm{2}}\right) \\ $$$${its}\:{value}\:{is}\:{sin}\left(\frac{{x}^{\mathrm{3}} }{\mathrm{3}!×\mathrm{2}}\right)\:{but}\:{by}\:{mistake}\:{i}\:{put}\:{it}\:{assin} \\ $$$${sin}\left(\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}\right) \\ $$$${so}\:{correct}\:{ans}\:{is} \\ $$$$=\frac{{lim}}{{x}\rightarrow\mathrm{0}}\frac{\mathrm{2}{sin}\left(\frac{{x}^{\mathrm{3}} }{\mathrm{3}!×\mathrm{2}}\right)}{\frac{{x}^{\mathrm{3}} }{\mathrm{3}!×\mathrm{2}}×\mathrm{3}!×\mathrm{2}} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}!×\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$ \\ $$

Commented by rahul 19 last updated on 07/May/18

Thank you sir! There is also an option for "edit post" ��

Answered by MJS last updated on 06/May/18

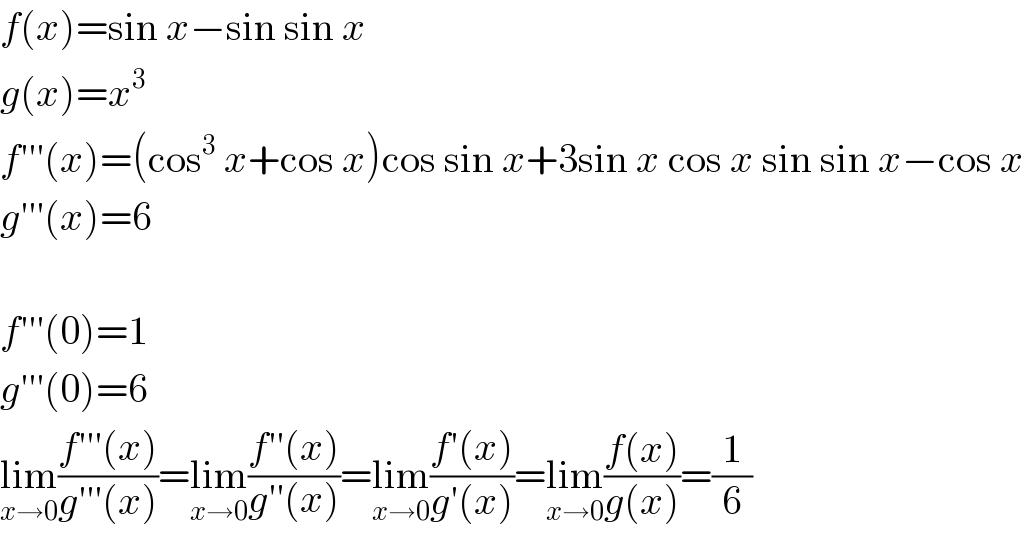
f(x)=sin x−sin sin x g(x)=x^3 f′′′(x)=(cos^3 x+cos x)cos sin x+3sin x cos x sin sin x−cos x g′′′(x)=6 f′′′(0)=1 g′′′(0)=6 lim_(x→0) ((f′′′(x))/(g′′′(x)))=lim_(x→0) ((f′′(x))/(g′′(x)_ ))=lim_(x→0) ((f′(x))/(g′(x)))=lim_(x→0) ((f(x))/(g(x)))=(1/6)

$${f}\left({x}\right)=\mathrm{sin}\:{x}−\mathrm{sin}\:\mathrm{sin}\:{x} \\ $$$${g}\left({x}\right)={x}^{\mathrm{3}} \\ $$$${f}'''\left({x}\right)=\left(\mathrm{cos}^{\mathrm{3}} \:{x}+\mathrm{cos}\:{x}\right)\mathrm{cos}\:\mathrm{sin}\:{x}+\mathrm{3sin}\:{x}\:\mathrm{cos}\:{x}\:\mathrm{sin}\:\mathrm{sin}\:{x}−\mathrm{cos}\:{x} \\ $$$${g}'''\left({x}\right)=\mathrm{6} \\ $$$$ \\ $$$${f}'''\left(\mathrm{0}\right)=\mathrm{1} \\ $$$${g}'''\left(\mathrm{0}\right)=\mathrm{6} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{f}'''\left({x}\right)}{{g}'''\left({x}\right)}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{f}''\left({x}\right)}{{g}''\left({x}\underset{} {\right)}}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{f}'\left({x}\right)}{{g}'\left({x}\right)}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{f}\left({x}\right)}{{g}\left({x}\right)}=\frac{\mathrm{1}}{\mathrm{6}} \\ $$

Commented by rahul 19 last updated on 07/May/18

Thank you sir !

Terms of Service

Privacy Policy

Contact: info@tinkutara.com