
Question and Answers Forum
Question Number 34562 by math khazana by abdo last updated on 08/May/18
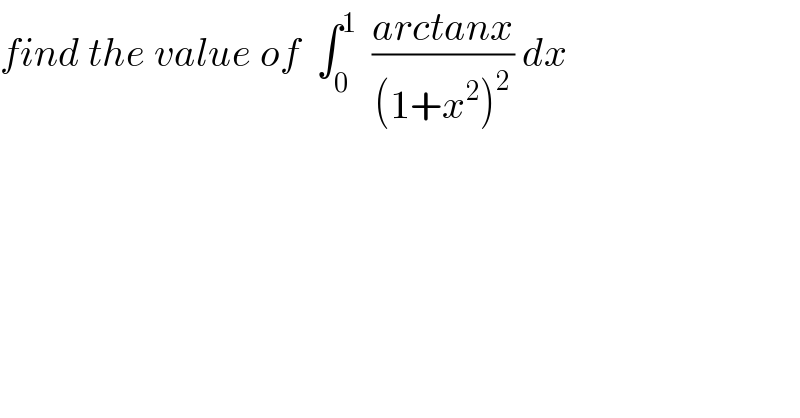
Commented by math khazana by abdo last updated on 08/May/18
![we have proved that ∫ ((arctanx)/((1+x^2 )^2 ))dx=(1/4) (arctanx)^2 +(1/4)sin(2arctanx)+k⇒ ∫_0 ^1 ((arctanx)/((1+x^2 )^2 ))dx=[(1/4)(arctanx)^2 +(1/4)sin(2arctanx)]_0 ^1 =(1/4)((π/4))^2 +(1/4)sin((π/2)) = (π^2 /(64)) +(1/4) .](Q34580.png)
Answered by tanmay.chaudhury50@gmail.com last updated on 08/May/18
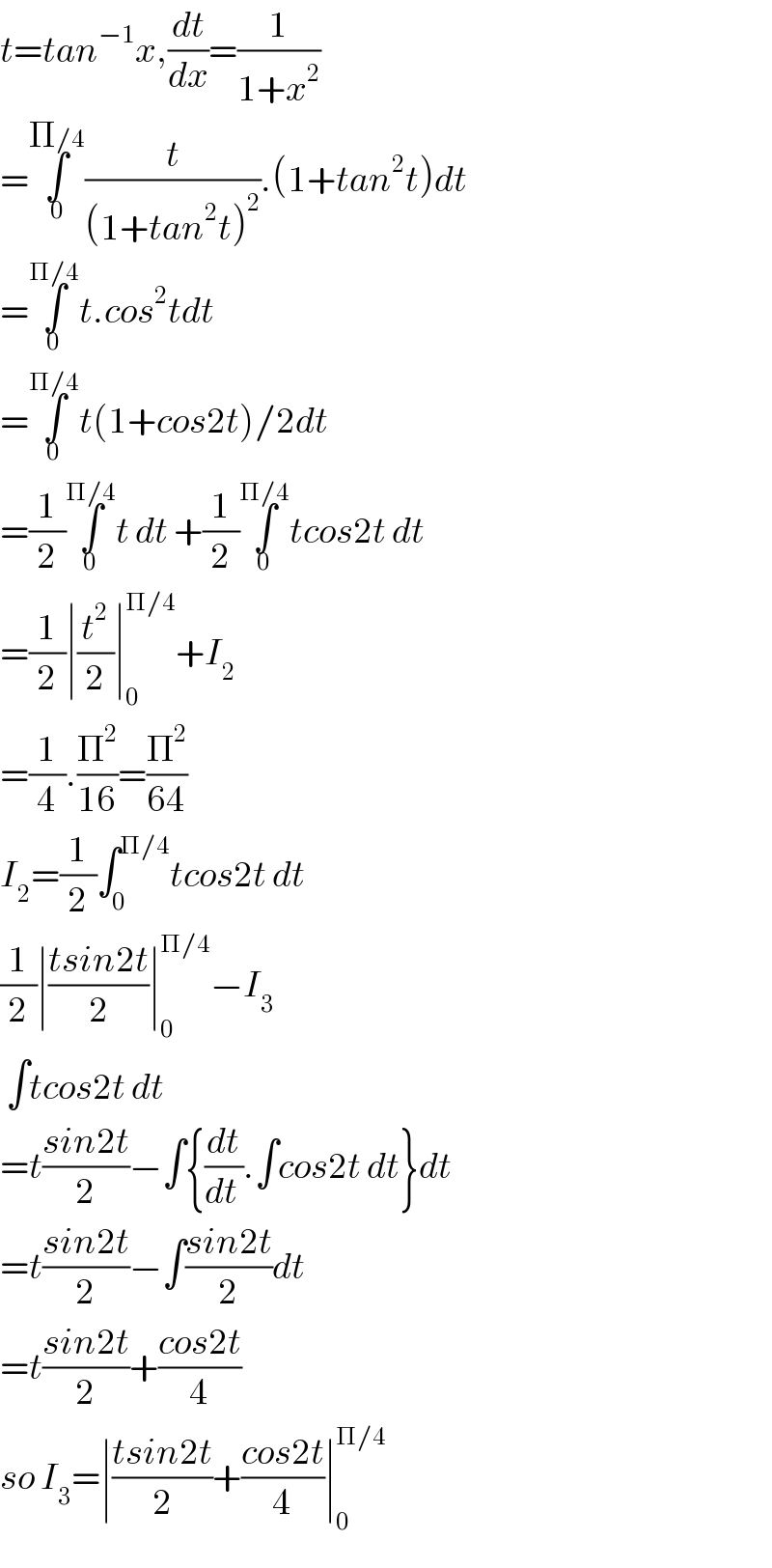
| ||
Question and Answers Forum | ||
Question Number 34562 by math khazana by abdo last updated on 08/May/18 | ||
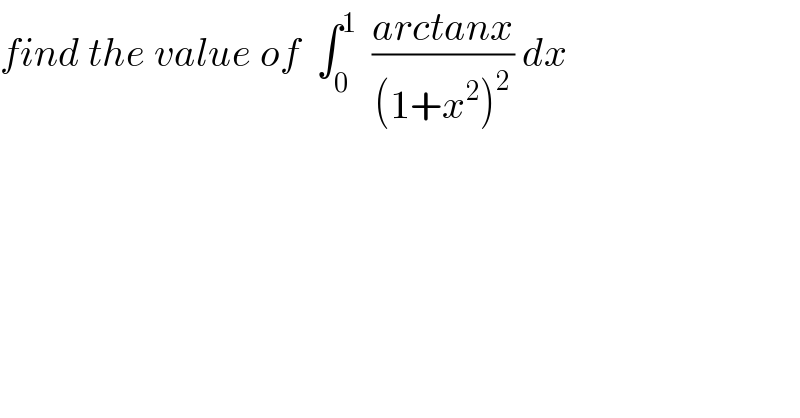 | ||
Commented by math khazana by abdo last updated on 08/May/18 | ||
![we have proved that ∫ ((arctanx)/((1+x^2 )^2 ))dx=(1/4) (arctanx)^2 +(1/4)sin(2arctanx)+k⇒ ∫_0 ^1 ((arctanx)/((1+x^2 )^2 ))dx=[(1/4)(arctanx)^2 +(1/4)sin(2arctanx)]_0 ^1 =(1/4)((π/4))^2 +(1/4)sin((π/2)) = (π^2 /(64)) +(1/4) .](Q34580.png) | ||
Answered by tanmay.chaudhury50@gmail.com last updated on 08/May/18 | ||
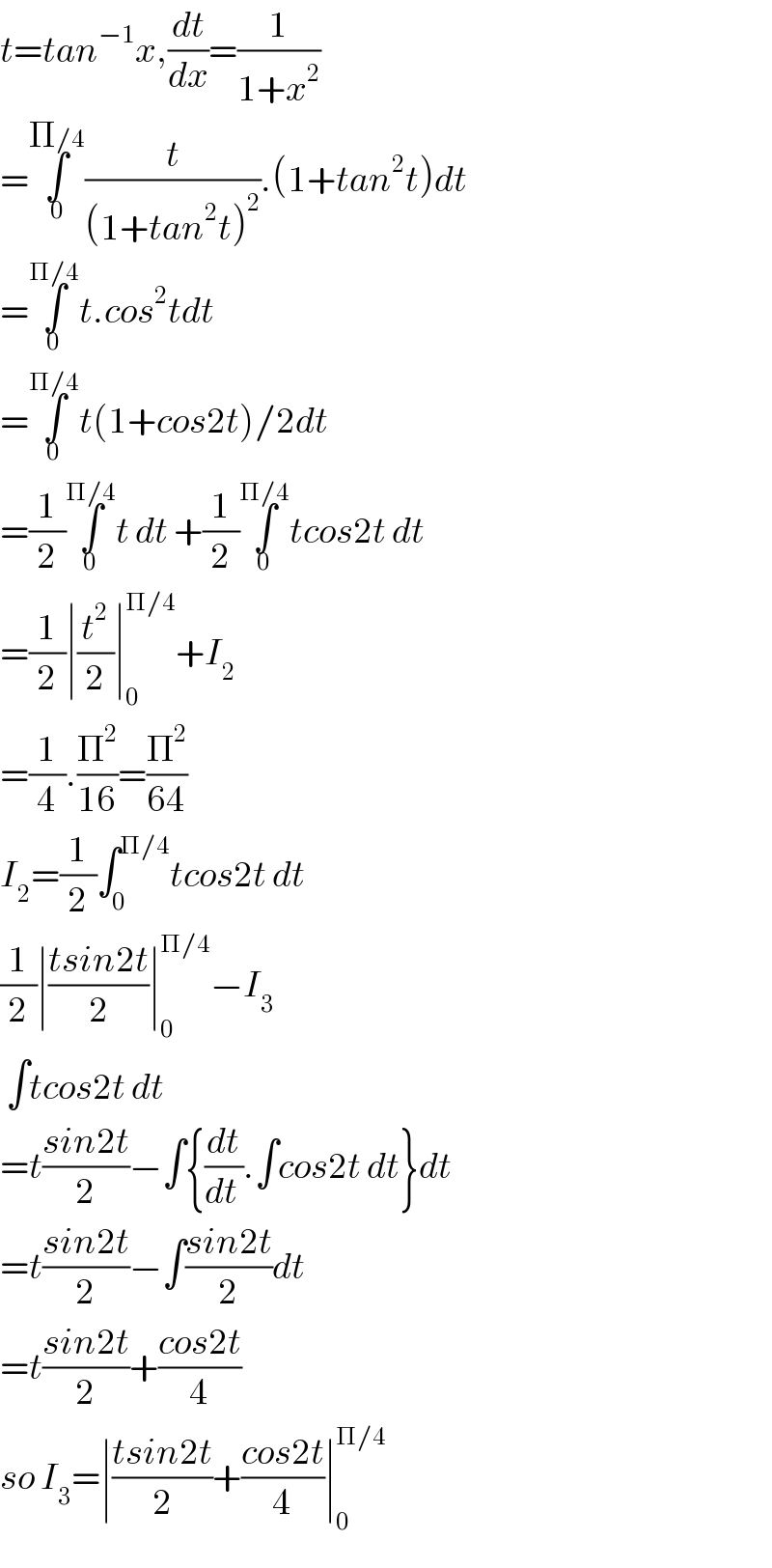 | ||
| ||