Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 34634 by abdo mathsup 649 cc last updated on 09/May/18

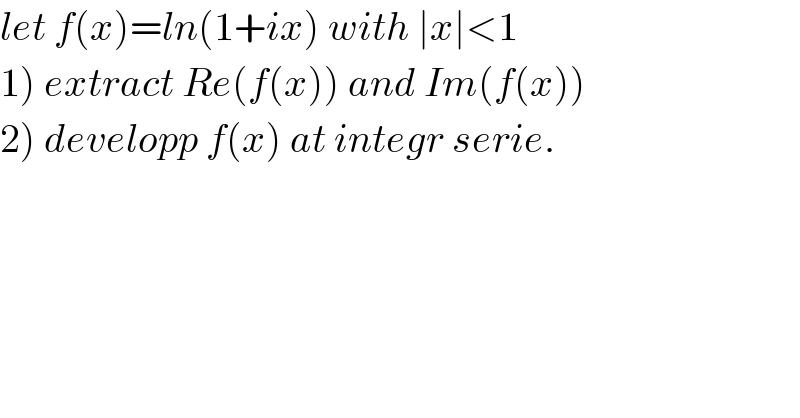
let f(x)=ln(1+ix) with ∣x∣<1 1) extract Re(f(x)) and Im(f(x)) 2) developp f(x) at integr serie.

$${let}\:{f}\left({x}\right)={ln}\left(\mathrm{1}+{ix}\right)\:{with}\:\mid{x}\mid<\mathrm{1} \\ $$ $$\left.\mathrm{1}\right)\:{extract}\:{Re}\left({f}\left({x}\right)\right)\:{and}\:{Im}\left({f}\left({x}\right)\right) \\ $$ $$\left.\mathrm{2}\right)\:{developp}\:{f}\left({x}\right)\:{at}\:{integr}\:{serie}. \\ $$

Commented bymath khazana by abdo last updated on 10/May/18

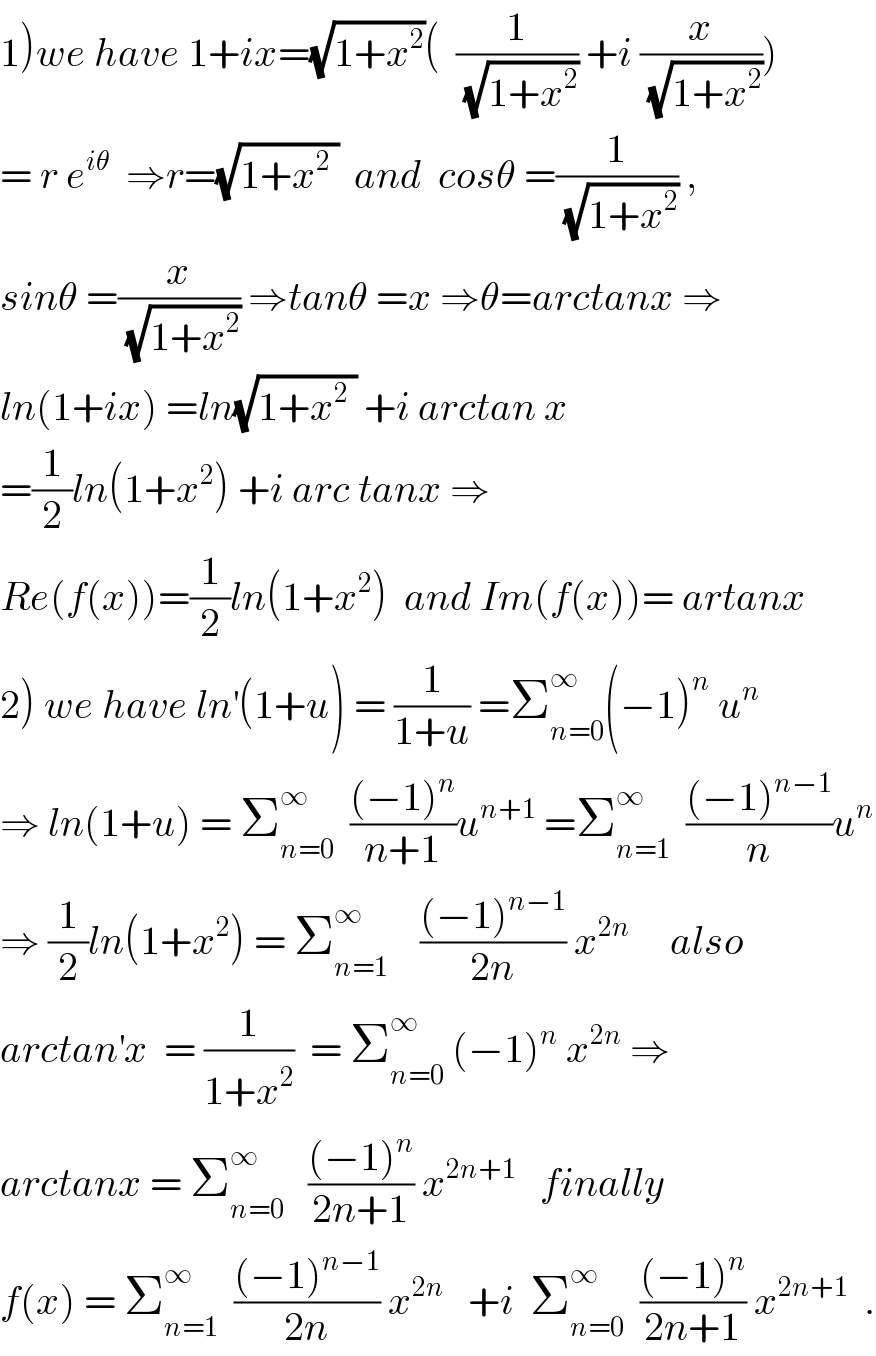
1)we have 1+ix=(√(1+x^2 ))( (1/(√(1+x^2 ))) +i (x/(√(1+x^2 )))) = r e^(iθ) ⇒r=(√(1+x^2 )) and cosθ =(1/(√(1+x^2 ))) , sinθ =(x/(√(1+x^2 ))) ⇒tanθ =x ⇒θ=arctanx ⇒ ln(1+ix) =ln(√(1+x^2 )) +i arctan x =(1/2)ln(1+x^2 ) +i arc tanx ⇒ Re(f(x))=(1/2)ln(1+x^2 ) and Im(f(x))= artanx 2) we have ln^′ (1+u) = (1/(1+u)) =Σ_(n=0) ^∞ (−1)^n u^n ⇒ ln(1+u) = Σ_(n=0) ^∞ (((−1)^n )/(n+1))u^(n+1) =Σ_(n=1) ^∞ (((−1)^(n−1) )/n)u^n ⇒ (1/2)ln(1+x^2 ) = Σ_(n=1) ^∞ (((−1)^(n−1) )/(2n)) x^(2n) also arctan^′ x = (1/(1+x^2 )) = Σ_(n=0) ^∞ (−1)^n x^(2n) ⇒ arctanx = Σ_(n=0) ^∞ (((−1)^n )/(2n+1)) x^(2n+1) finally f(x) = Σ_(n=1) ^∞ (((−1)^(n−1) )/(2n)) x^(2n) +i Σ_(n=0) ^∞ (((−1)^n )/(2n+1)) x^(2n+1) .

$$\left.\mathrm{1}\right){we}\:{have}\:\mathrm{1}+{ix}=\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\left(\:\:\frac{\mathrm{1}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:+{i}\:\frac{{x}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\right) \\ $$ $$=\:{r}\:{e}^{{i}\theta} \:\:\Rightarrow{r}=\sqrt{\mathrm{1}+{x}^{\mathrm{2}} \:}\:\:{and}\:\:{cos}\theta\:=\frac{\mathrm{1}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:, \\ $$ $${sin}\theta\:=\frac{{x}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:\Rightarrow{tan}\theta\:={x}\:\Rightarrow\theta={arctanx}\:\Rightarrow \\ $$ $${ln}\left(\mathrm{1}+{ix}\right)\:={ln}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} \:}\:+{i}\:{arctan}\:{x} \\ $$ $$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\:+{i}\:{arc}\:{tanx}\:\Rightarrow \\ $$ $${Re}\left({f}\left({x}\right)\right)=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\:\:{and}\:{Im}\left({f}\left({x}\right)\right)=\:{artanx} \\ $$ $$\left.\mathrm{2}\right)\:{we}\:{have}\:{ln}^{'} \left(\mathrm{1}+{u}\right)\:=\:\frac{\mathrm{1}}{\mathrm{1}+{u}}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} \:{u}^{{n}} \\ $$ $$\Rightarrow\:{ln}\left(\mathrm{1}+{u}\right)\:=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}+\mathrm{1}}{u}^{{n}+\mathrm{1}} \:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}{u}^{{n}} \\ $$ $$\Rightarrow\:\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\:=\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{\mathrm{2}{n}}\:{x}^{\mathrm{2}{n}} \:\:\:\:\:{also} \\ $$ $${arctan}^{'} {x}\:\:=\:\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }\:\:=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} \:{x}^{\mathrm{2}{n}} \:\Rightarrow \\ $$ $${arctanx}\:=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{1}}\:{x}^{\mathrm{2}{n}+\mathrm{1}} \:\:\:{finally} \\ $$ $${f}\left({x}\right)\:=\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{\mathrm{2}{n}}\:{x}^{\mathrm{2}{n}} \:\:\:+{i}\:\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{1}}\:{x}^{\mathrm{2}{n}+\mathrm{1}} \:\:. \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 09/May/18

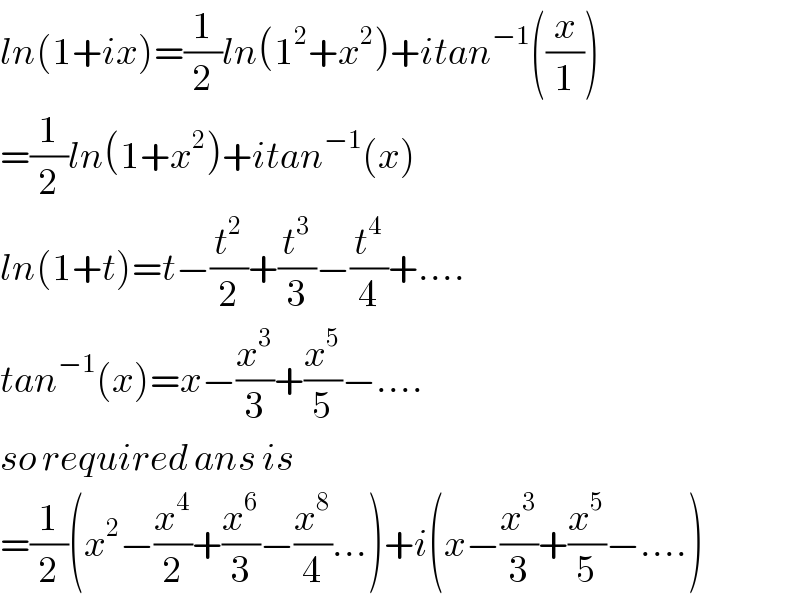
ln(1+ix)=(1/2)ln(1^2 +x^2 )+itan^(−1) ((x/1)) =(1/2)ln(1+x^2 )+itan^(−1) (x) ln(1+t)=t−(t^2 /2)+(t^3 /3)−(t^4 /4)+.... tan^(−1) (x)=x−(x^3 /3)+(x^5 /5)−.... so required ans is =(1/2)(x^2 −(x^4 /2)+(x^6 /3)−(x^8 /4)...)+i(x−(x^3 /3)+(x^5 /5)−....)

$${ln}\left(\mathrm{1}+{ix}\right)=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}^{\mathrm{2}} +{x}^{\mathrm{2}} \right)+{itan}^{−\mathrm{1}} \left(\frac{{x}}{\mathrm{1}}\right) \\ $$ $$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)+{itan}^{−\mathrm{1}} \left({x}\right) \\ $$ $${ln}\left(\mathrm{1}+{t}\right)={t}−\frac{{t}^{\mathrm{2}} }{\mathrm{2}}+\frac{{t}^{\mathrm{3}} }{\mathrm{3}}−\frac{{t}^{\mathrm{4}} }{\mathrm{4}}+.... \\ $$ $${tan}^{−\mathrm{1}} \left({x}\right)={x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{{x}^{\mathrm{5}} }{\mathrm{5}}−.... \\ $$ $${so}\:{required}\:{ans}\:{is} \\ $$ $$=\frac{\mathrm{1}}{\mathrm{2}}\left({x}^{\mathrm{2}} −\frac{{x}^{\mathrm{4}} }{\mathrm{2}}+\frac{{x}^{\mathrm{6}} }{\mathrm{3}}−\frac{{x}^{\mathrm{8}} }{\mathrm{4}}...\right)+{i}\left({x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{{x}^{\mathrm{5}} }{\mathrm{5}}−....\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com