Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 3467 by Rasheed Soomro last updated on 13/Dec/15

Prove that in general trisection of an angle is impossible with only ruler and compass.

$${Prove}\:{that}\:{in}\:{general}\:{trisection}\:{of}\:{an} \\ $$$${angle}\:{is}\:{impossible}\:{with}\:{only}\:{ruler} \\ $$$${and}\:{compass}. \\ $$

Commented by prakash jain last updated on 13/Dec/15

sin 3x=sin (2x+x)=sin 2xcos x+cos 2xsin x =2sin x(1−sin^2 x)+(1−2sin^2 x)sin x =3sin x−4sin^3 x If we able to construct trisect any angle 3x. If 3x=30°, sin 10°=y (1/2)=3y−4y^3 8y^3 −6y−1=0 2y=u u^3 −3u+1=0 ...(A) From rational roots theorem, ±1 are only possible rational root which are not possible. try=a+b(√c) (a,b,c∈Q), second root will be a−b(√c) third root is say α. (x−(a+b(√c)))(x−(a−b(√c))(x−α)=u^3 −3u+1 −α(a+b(√c))(a−b(√c))=1⇒α is rational. Since the equation has no rational roots, it has no root which are of the form a+b(√c) (a,b,c∈Q).

$$\mathrm{sin}\:\mathrm{3}{x}=\mathrm{sin}\:\left(\mathrm{2}{x}+{x}\right)=\mathrm{sin}\:\mathrm{2}{x}\mathrm{cos}\:{x}+\mathrm{cos}\:\mathrm{2}{x}\mathrm{sin}\:{x} \\ $$$$=\mathrm{2sin}\:{x}\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} {x}\right)+\left(\mathrm{1}−\mathrm{2sin}^{\mathrm{2}} {x}\right)\mathrm{sin}\:{x} \\ $$$$=\mathrm{3sin}\:{x}−\mathrm{4sin}^{\mathrm{3}} {x} \\ $$$$\mathrm{If}\:\mathrm{we}\:\mathrm{able}\:\mathrm{to}\:\mathrm{construct}\:\mathrm{trisect}\:\mathrm{any}\:\mathrm{angle} \\ $$$$\mathrm{3}{x}. \\ $$$$\mathrm{If}\:\mathrm{3}{x}=\mathrm{30}°,\:\mathrm{sin}\:\mathrm{10}°={y} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{3}{y}−\mathrm{4}{y}^{\mathrm{3}} \\ $$$$\mathrm{8}{y}^{\mathrm{3}} −\mathrm{6}{y}−\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{2}{y}={u} \\ $$$${u}^{\mathrm{3}} −\mathrm{3}{u}+\mathrm{1}=\mathrm{0}\:\:\:\:...\left(\mathrm{A}\right) \\ $$$$\mathrm{From}\:\mathrm{rational}\:\mathrm{roots}\:\mathrm{theorem},\:\pm\mathrm{1}\:\mathrm{are}\:\mathrm{only} \\ $$$$\mathrm{possible}\:\mathrm{rational}\:\mathrm{root}\:\mathrm{which}\:\mathrm{are}\:\mathrm{not}\:\mathrm{possible}. \\ $$$$\mathrm{try}={a}+{b}\sqrt{{c}}\:\left({a},{b},{c}\in\mathbb{Q}\right),\:\mathrm{second}\:\mathrm{root}\:\mathrm{will}\:\mathrm{be}\:{a}−{b}\sqrt{{c}} \\ $$$$\mathrm{third}\:\mathrm{root}\:\mathrm{is}\:\mathrm{say}\:\alpha. \\ $$$$\left({x}−\left({a}+{b}\sqrt{{c}}\right)\right)\left({x}−\left({a}−{b}\sqrt{{c}}\right)\left({x}−\alpha\right)={u}^{\mathrm{3}} −\mathrm{3}{u}+\mathrm{1}\right. \\ $$$$−\alpha\left({a}+{b}\sqrt{{c}}\right)\left({a}−{b}\sqrt{{c}}\right)=\mathrm{1}\Rightarrow\alpha\:\mathrm{is}\:\mathrm{rational}. \\ $$$$\mathrm{Since}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{has}\:\mathrm{no}\:\mathrm{rational}\:\mathrm{roots}, \\ $$$$\mathrm{it}\:\mathrm{has}\:\mathrm{no}\:\mathrm{root}\:\mathrm{which}\:\mathrm{are}\:\mathrm{of}\:\mathrm{the}\:\mathrm{form} \\ $$$${a}+{b}\sqrt{{c}}\:\left({a},{b},{c}\in\mathbb{Q}\right). \\ $$

Answered by prakash jain last updated on 13/Dec/15

As sin 10° ∉Q and not of form a+b(√c), sin 10° cannot be drawn using ruler and compass. So 30° cannot be trisected.

$$\mathrm{As}\:\mathrm{sin}\:\mathrm{10}°\:\notin\mathbb{Q}\:\mathrm{and}\:\mathrm{not}\:\mathrm{of}\:\mathrm{form}\:{a}+{b}\sqrt{{c}},\:\mathrm{sin}\:\mathrm{10}°\:\mathrm{cannot} \\ $$$$\mathrm{be}\:\mathrm{drawn}\:\mathrm{using}\:\mathrm{ruler}\:\mathrm{and}\:\mathrm{compass}. \\ $$$$\mathrm{So}\:\mathrm{30}°\:\mathrm{cannot}\:\mathrm{be}\:\mathrm{trisected}. \\ $$

Commented by prakash jain last updated on 13/Dec/15

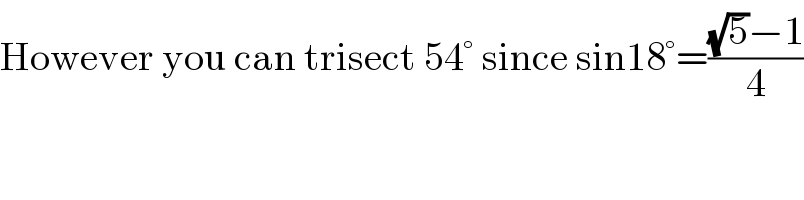
However you can trisect 54° since sin18°=(((√5)−1)/4)

$$\mathrm{However}\:\mathrm{you}\:\mathrm{can}\:\mathrm{trisect}\:\mathrm{54}°\:\mathrm{since}\:\mathrm{sin18}°=\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com