
Question and Answers Forum
Previous in Relation and Functions Next in Relation and Functions
Question Number 34692 by math khazana by abdo last updated on 09/May/18
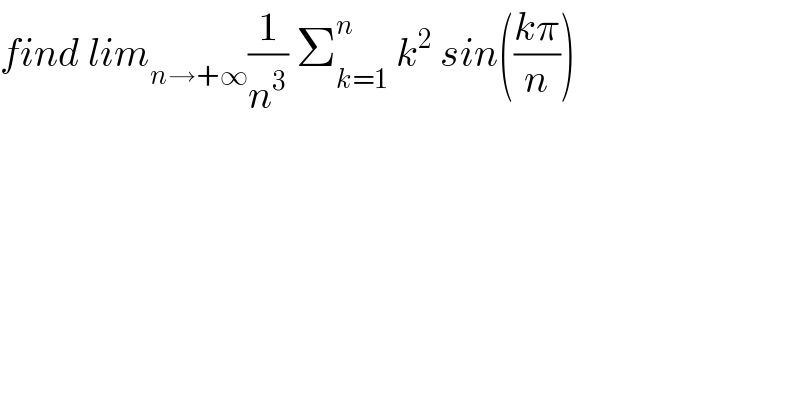
Commented by math khazana by abdo last updated on 11/May/18
![let put S_n = (1/n^3 ) Σ_(k=1) ^n k^2 sin(((kπ)/n)) S_n = (1/n) Σ_(k=1) ^n ((k/n))^2 sin(((kπ)/n))→_(n→+∞) ∫_0 ^1 x^2 sinx dx let integrate by parts I =∫_0 ^1 x^2 sinxdx =[−x^2 cosx]_0 ^1 +∫_0 ^1 2x cosxdx =−cos(1) +2 { [xsinx]_0 ^1 −∫_0 ^1 sinxdx} = −cos(1) +2{ sin(1) +[cosx]_0 ^1 } =−cos(1) +2{ sin(1) +cos(1)−1} =2sin(1) +cos(1) −2 lim_(n→+∞) S_n = 2sin(1) +cos(1) −2 .](Q34828.png)
| ||
Question and Answers Forum | ||
Previous in Relation and Functions Next in Relation and Functions | ||
Question Number 34692 by math khazana by abdo last updated on 09/May/18 | ||
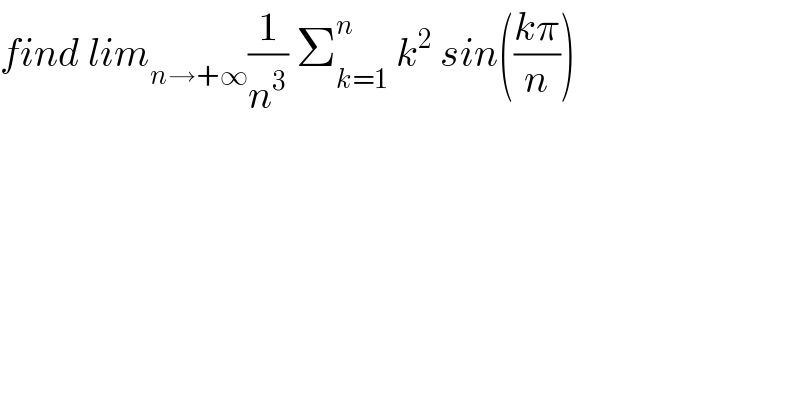 | ||
Commented by math khazana by abdo last updated on 11/May/18 | ||
![let put S_n = (1/n^3 ) Σ_(k=1) ^n k^2 sin(((kπ)/n)) S_n = (1/n) Σ_(k=1) ^n ((k/n))^2 sin(((kπ)/n))→_(n→+∞) ∫_0 ^1 x^2 sinx dx let integrate by parts I =∫_0 ^1 x^2 sinxdx =[−x^2 cosx]_0 ^1 +∫_0 ^1 2x cosxdx =−cos(1) +2 { [xsinx]_0 ^1 −∫_0 ^1 sinxdx} = −cos(1) +2{ sin(1) +[cosx]_0 ^1 } =−cos(1) +2{ sin(1) +cos(1)−1} =2sin(1) +cos(1) −2 lim_(n→+∞) S_n = 2sin(1) +cos(1) −2 .](Q34828.png) | ||