
Question and Answers Forum
Question Number 34717 by abdo mathsup 649 cc last updated on 10/May/18
![let I_n = ∫∫_([(1/n),n]^2 ) (((√(xy)) dxdy)/(2 +x^2 +y^2 )) find lim I_n when n→+∞.](Q34717.png)
Commented by prof Abdo imad last updated on 11/May/18
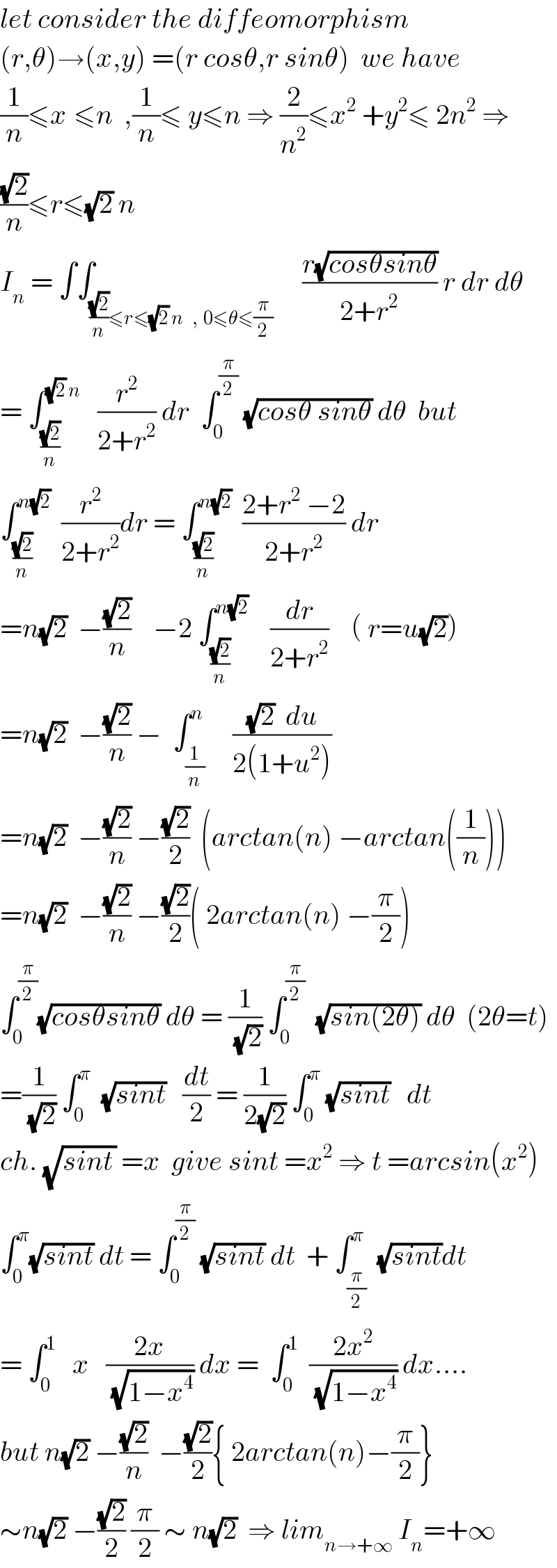
| ||
Question and Answers Forum | ||
Question Number 34717 by abdo mathsup 649 cc last updated on 10/May/18 | ||
![let I_n = ∫∫_([(1/n),n]^2 ) (((√(xy)) dxdy)/(2 +x^2 +y^2 )) find lim I_n when n→+∞.](Q34717.png) | ||
Commented by prof Abdo imad last updated on 11/May/18 | ||
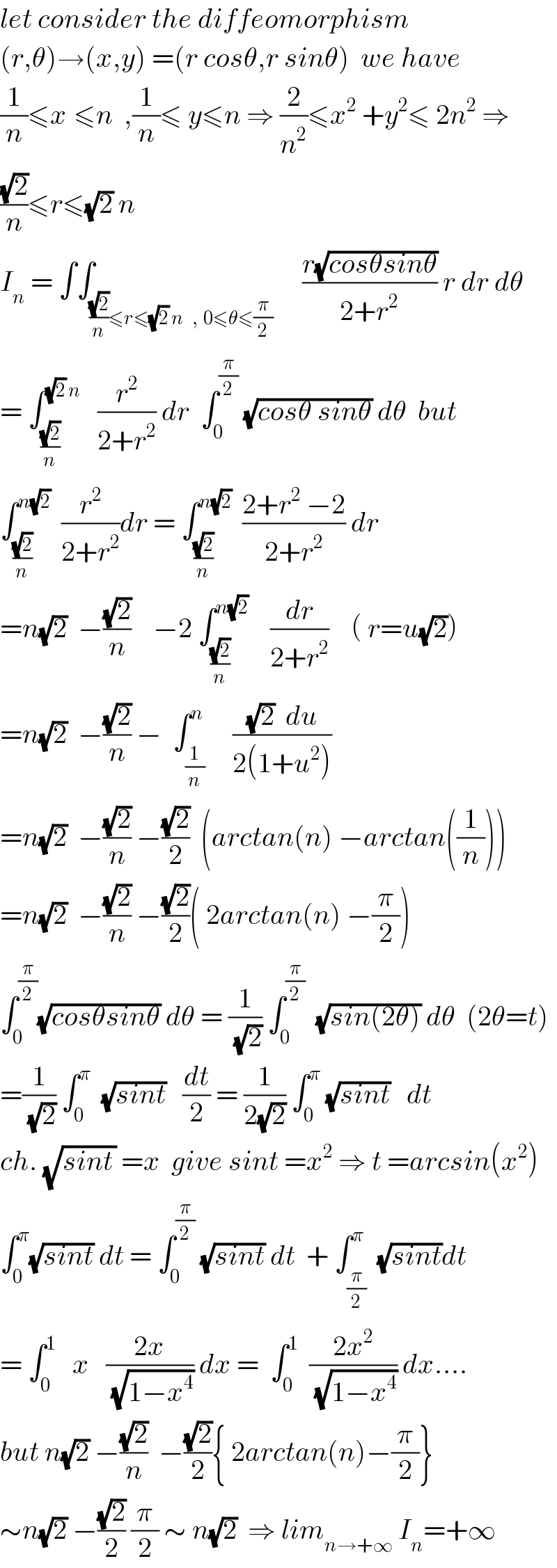 | ||